群 环 域
群 group
G是一个集合,在此集合上定义代数运算*,若满足下列公理,则称G为群。
1.封闭性 a ∈ G , b ∈ G a\in G,b\in G a∈G,b∈G=> a ∗ b ∈ G a*b\in G a∗b∈G
2.G中有恒等元素e,使得任何元素与e运算均为元素本身(如:单位矩阵、加法的0,乘法的1)
3.G的每个非0元素都有逆元素,使得元素*逆元素=e(如:加法中的负数,乘法中的倒数)
4.满足结合律
阿贝尔群(可交换群):
1.满足群的四条公理
2.满足交换律(矩阵不满足)
例:(7,3)码在模2加法下构成群,(n,k)码又称群码
0000000 单位元
0011101
0100111
0111010
1001110
1010011
1101001
1110100
封闭性可验证。存在e。每个元素的逆都是他们本身。模2加法相当于异或,满足结合律。故此运算为群。
线性分组编码
环 Ring
R是一个集合,在其上定义两种代数运算+、*,若满足下列公理则称为环
1.+下构成群
2.*下满足封闭性
3. *下满足结合律
4. 分配律成立(包括左分配和右分配)
左分配:a(b+c)=ab+ac
右分配:(b+c)a=ba+ca
如:矩阵的乘对加满足分配律
e.g.
整数集合是环,加法和乘法构成整数环
实系数的多项式环
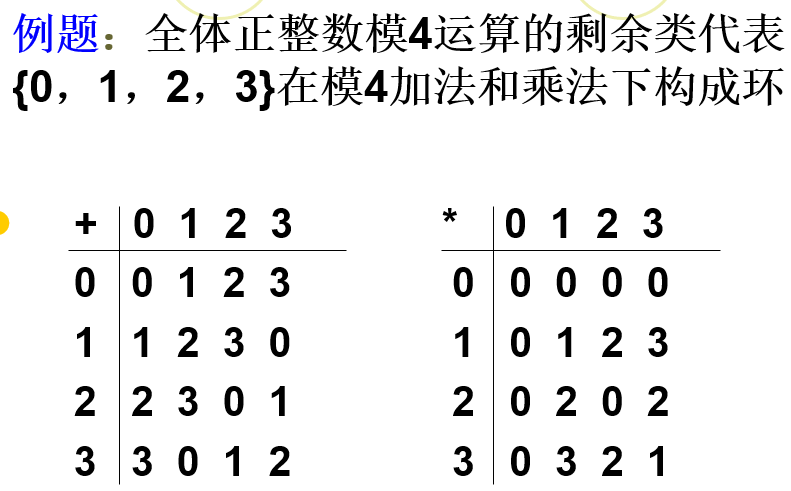
域 Field
在F集合上定义两种代数运算+和*,若满足下列公理,则F称为域
1.在加法下构成群
2.全体非0元素构成交换乘群(=加法和乘法都成群)
3.对加法和乘法分配律成立
域是有单位元素、非0元素有逆元素的交换环
e,g,以p=3为模的剩余类全体{0,1,2}构成域
有限域:域中元素数目是有限的; 记为: GF(q)q为域的阶,称为q元域;
无限域:域中元素的数目是无限的;
域的阶:域中元素的数目;
GF(2)为二元域,是最小的域
实际应用中,q的量级是 2 1024 2^{1024} 21024,非常巨大
数域包括 复数域、实数域、有理数域
二元域上的多项式
系数取自GF(2),含有一个未定元x的多项式称为GF(2)上的多项式,用f(x)表示。
多项式的加法:同幂次的系数相加
多项式的乘法:正常展开
相加时使用模2加法,即异或,即不进位的加法
x 2 − x = x 2 + ( 1 ) − 1 x = x 2 + x x^2-x=x^2+(1)^{-1}x=x^2+x x2−x=x2+(1)−1x=x2+x
二元域上的既约多项式
f(x)是次数>0的多项式,若除了1和多项式本身以外,不能再被GF(2)上的其他多项式除尽,则称为f(x)是二元域上的既约多项式(不可约多项式)。
即,不能分解为两个多项式的乘积
e.g.m=4,f(x)= x 4 + x + 1 x^4+x+1 x4+x+1 等价于五元向量(1,0,0,1,1)
f(x)不能在GF(2)上分解,但可以在更大的范围域内分解
定义:如果有两个域F1,F2,如果 F 1 ⊂ F 2 F_1\subset F_2 F1⊂F2,则F2是F1的扩域。
在域F1上的一个不可约多项式,在其扩域F2上可能有根,如果f(x)在F2上有根 α \alpha α,则在F2上f(x)有分解因子 ( x − α ) (x-\alpha ) (x−α)
e.g. x 2 + 1 x^2+1 x2+1在R内不可分解,但在复数域上可以分解为(x+i)(x-i)
设P(x)是GF(2)上的m次既约多项式,GF(2)上所有次数小于m的多项式的全体,在模2加法、模P(x)乘法运算下构成一个 2 m 2^m 2m阶的有限域,称为GF( 2 m 2^m 2m),GF(2)是扩域GF( 2 m 2^m 2m)的基域。扩域GF( 2 m 2^m 2m)中有 2 m 2^m 2m个元素,每个元素形如: a m − 1 x m − 1 + a m − 2 x m − 2 + . . . + a 1 x + a 0 a_{m-1}x^{m-1}+a_{m-2}x^{m-2}+...+a_1x+a_0 am−1xm−1+am−2xm−2+...+a1x+a0,可记为m维二元向量的形式( a m − 1 , a m − 2 , . . . , a 1 , a 0 a_{m-1},a_{m-2},...,a_1,a_0 am−1,am−2,...,a1,a0)
设P(x)是GF(2)上的一个m次既约多项式,如果构成的扩域GF( 2 m 2^m 2m)中的全体非0多项式元素对模P(x)乘法构成乘法循环群,即,存在GF( 2 m 2^m 2m)的一个非0元素 α ∈ G F ( 2 m ) \alpha \in GF(2^m) α∈GF(2m),它的各次幂 α 0 , α 1 , . . . , α 2 m − 2 \alpha ^0,\alpha ^1,...,\alpha ^{2^m-2} α0,α1,...,α2m−2恰好构成扩域GF( 2 m 2^m 2m)的全部非零元素,则称P(x)是GF(2)上的一个m次本原多项式。有:
1. α \alpha α是GF(2)的一个本原元
2. α \alpha α是GF(2)上的既约多项式P(x)在扩域GF( 2 m 2^m 2m)中的一个根
3.GF(2)上的本原多项式P(x)在扩域GF( 2 m 2^m 2m)中的任何一个根都是本原元
e.g.

( 0 , 1 , α , α 2 , . . . . , α 14 ) (0,1,\alpha,\alpha^2,....,\alpha^{14}) (0,1,α,α2,....,α14)构成域,称为GF(2)的4次扩域。域的阶为16,记为GF( 2 4 2^4 24)。也构成循环群。
求逆:扩展欧几里得算法
对称加密算法 AES
AES(Advanced Encryption Standard) 之 Rijndael算法
迭代分组密码,分组长度为128b,密码长度为128/192/256b,相应的轮数r为10/12/14
讨论密钥长度为128b,分组长度为128b的情况
128b的消息被分为16个字节,每字节8位,记为InputBlock=m0,m1,m2…m15
密钥分组如下:InputKey=k0,k1,k2…k15
内部数据结构表示为一个4x4的矩阵:
I n p u t B l o c k = [ m 0 m 4 m 8 m 12 m 1 m 5 m 9 m 13 m 2 m 6 m 10 m 14 m 3 m 7 m 11 m 15 ] InputBlock=\begin{bmatrix} m0& m4& m8& m12\\ m1& m5& m9& m13\\ m2& m6& m10& m14\\ m3& m7& m11& m15 \end{bmatrix} InputBlock= m0m1m2m3m4m5m6m7m8m9m10m11m12m13m14m15
I n p u t K e y = [ k 0 k 4 k 8 k 12 k 1 k 5 k 9 k 13 k 2 k 6 k 10 k 14 k 3 k 7 k 11 k 15 ] InputKey=\begin{bmatrix} k0& k4& k8& k12\\ k1& k5& k9& k13\\ k2& k6& k10& k14\\ k3& k7& k11& k15 \end{bmatrix} InputKey= k0k1k2k3k4k5k6k7k8k9k10k11k12k13k14k15
轮变换
Round(State,RoundKey)
State是轮消息矩阵,被看作输入和输出,RoundKey是轮密钥矩阵,由输入密钥通过密钥表导出,一轮的完成将导致State的元素改变状态。
每轮变换由四个不同的变换组成:
SubBytes(State)
模f(x)= x 8 + x 4 + x 3 + x + 1 x^8+x^4+x^3+x+1 x8+x4+x3+x+1得到扩域GF( 2 8 2^8 28),有256个元素。
SubBytes函数为State的每个字节(x)提供非线性变换,任一非0的字节x ∈ F 2 8 \in F_{2^8} ∈F28被下面的变换取代: y = A x − 1 + b y=Ax^{-1}+b y=Ax−1+b 。求逆体现了变换的非线性,A是可逆的,所以此变换可逆。

e.g.
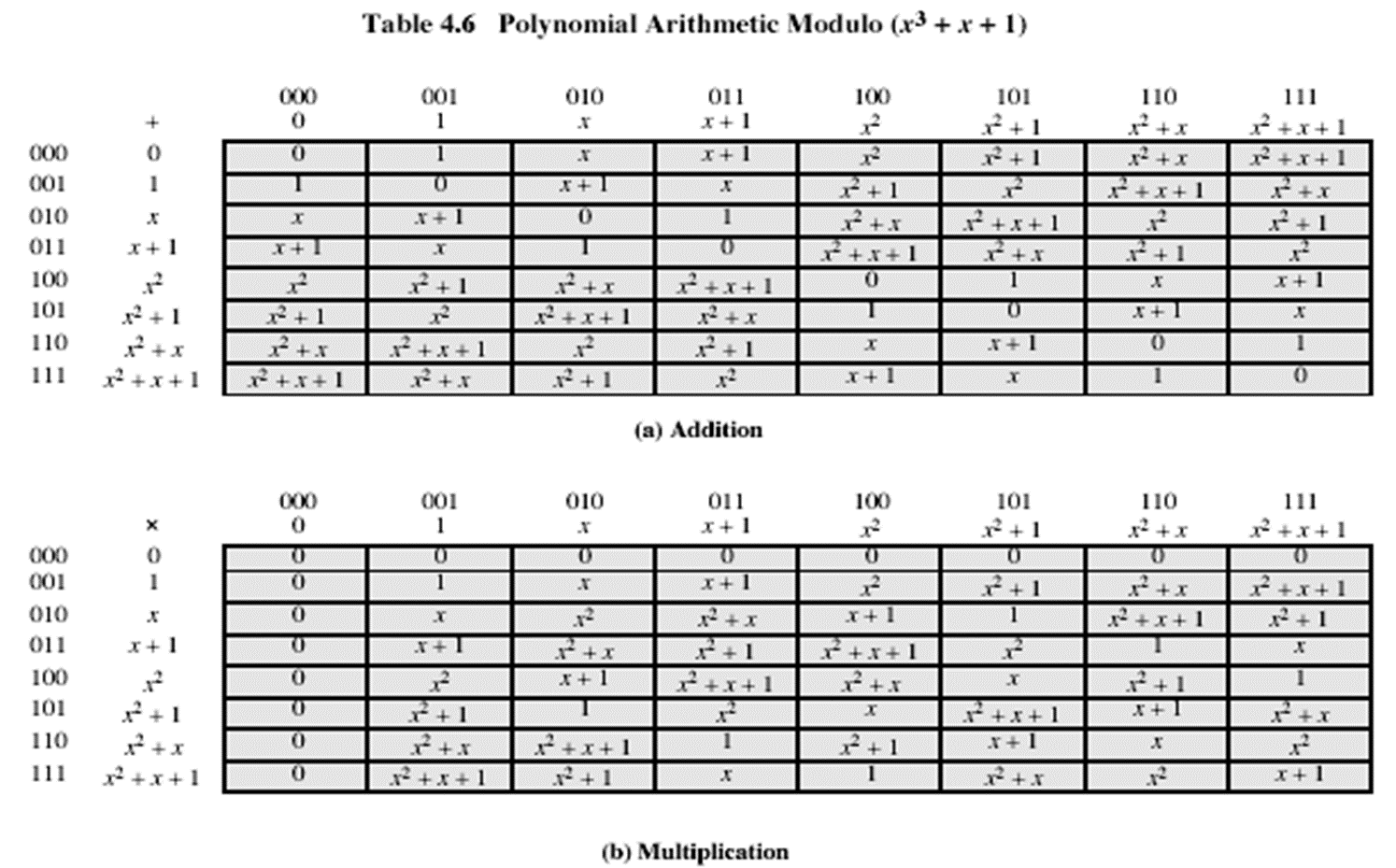
由于系数是0或1,因此可以将任何这样的多项式表示为比特串
加法是这些位串的XOR
乘法是移位&XOR
通过用不可约多项式的余数重复替换最高幂来实现模约简(也称为移位和XOR)
ShiftRows(State)

每行分别循环左移0,1,2,3位
MixColumns(State)
这个函数对State的每一列作用,迭代四次,下面仅仅描述对一列的作用:
令State的一列为: [ S 0 S 1 S 2 S 3 ] \begin{bmatrix} S_0\\ S_1\\ S_2\\ S_3 \end{bmatrix} S0S1S2S3 ,把这一列表示为三次多项式: s ( x ) = s 3 x 3 + s 2 x 2 + s 1 x + s 0 s(x)=s_3x^3+s_2x^2+s_1x+s_0 s(x)=s3x3+s2x2+s1x+s0,因为s(x)的系数是字节,也就是说是 F 2 8 F_2^8 F28域中的元素,所以这个多项式是 F 2 8 F_2^8 F28上的。
列s(x)上的运算定义为将这个多项式乘以一个固定的3次多项式c(x),然后模x4+1:
d ( x ) = c ( x ) × s ( x ) ( m o d x 4 + 1 ) d(x) = c(x) × s(x) (mod \ x^4+1) d(x)=c(x)×s(x)(mod x4+1)
c ( x ) = c 3 x 3 + c 2 x 2 + c 1 x + c 0 c(x)=c_3x^3+c_2x^2+c_1x+c_0 c(x)=c3x3+c2x2+c1x+c0
其中, x i ( m o d x 4 + 1 ) = x i m o d 4 x^i(mod \ x^4+1)=x^{imod4} xi(mod x4+1)=ximod4
Rijndeal给出:c3=“03”, c2=“01”, c1=“01”, c0=“02”
在乘积d(x)中,x2的系数是d2=c2s0+c1s1+c0s2+c3s3
上述乘法的系数可以写成以下矩阵乘法: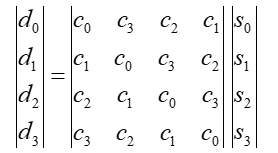
F 8 F_8 F8上,c(x)与 x 4 + 1 x^4+1 x4+1是互素的,所以在 F 8 ( x ) F_8(x) F8(x)中,逆 c ( x ) − 1 ( m o d x 4 + 1 ) c(x)^{-1} (modx^4+1) c(x)−1(modx4+1)是存在的。这等于说,上述矩阵变换是可逆的。
AddRoundKey(State, RoundKey)
这个函数是逐字节、逐比特地将RoundKey中的元素与State中的元素相加。这里的加,是F2中的加,也就是异或运算,是平凡可逆的。
不同轮的密钥比特是不同的。它们使用一个固定的“密钥表”导出密钥,每轮密钥不同,该“密钥表”是非秘密的。具体细节可参阅有关NIST的标准文件。
解密
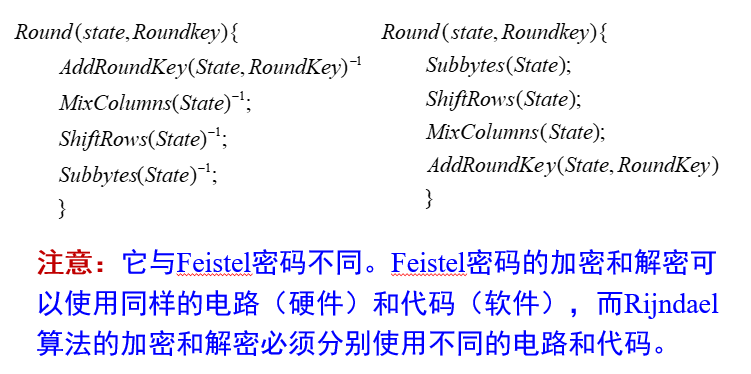
非对称加密算法 RSA
非对称,指的是加密和解密的密钥不同。
陷门单向函数
若函数f:A->B可逆(单射+满射),且满足对 x ∈ A x\in A x∈A,易于求解f(x),但由f(x)求x极为困难,则称为 单向函数。
陷门单项函数:
f z : A z − > B z , z ∈ Z f_z:A_z->B_z,z\in Z fz:Az−>Bz,z∈Z,Z是陷门信息集合。
1)在给定 z ∈ Z z\in Z z∈Z下容易找到一对算法 E z E_z Ez和 D z D_z Dz,使得对所有 x ∈ A x\in A x∈A,易于计算 f z f_z fz及其逆,即: f z ( x ) = E z ( x ) , D z ( f z ( x ) ) = x f_z(x)=E_z(x),D_z(f_z(x))=x fz(x)=Ez(x),Dz(fz(x))=x。
2)只给定 E z E_z Ez和 D z D_z Dz时,对所有 x ∈ A x\in A x∈A都很难从 y = f z ( x ) y=f_z(x) y=fz(x)中计算出x
单向函数是求逆困难的函数,而陷门单项函数是在不知道陷门信息下求逆困难、在知道陷门信息下求逆容易的函数。
用于构造双钥密码的单向函数
-
多项式求根
-
离散对数DL
-
大整数分解FAC
-
背包问题
-
赫尔曼问题 DHP
-
二次剩余问题QR
-
模n的平方问题 SQROOT