一直忙着金工实习+蓝桥杯,好久没有看图论了,今天就小试几题享受下被虐的快感。
1.最短路+拓扑

首先来几个结论:
1.最短路图没有环(可以用反证法证明)
2.dis[u]+edge[u,v]=dis[v],那么u,v端点的边一定在最短路图上。
因此,我们就可以先枚举起始点跑SPFA,然后把最短路找出来,假如一个边的端点为u,v,那么经过它的为cnt1[u]*cnt2[v],cnt1为正着最短路图上过u的边,cnt2为反着(注意到v结束也是一种,所以结尾后+1)。
因此,我们求两边拓扑排序即可,下面是AC代码(这里正反图用奇偶存储来区别):
#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;const int N=1502;
const int M=100010;
bool vis[N];
int dis[N],in1[N],in2[N],cnt1[N],cnt2[N];
int n,m,u,v,w,head[N],is[M],cnt=1;
int ans[M];
struct node{int dian,next,zhi;
}edge[M];
void add(int u,int v,int w){//i&1为反图 edge[++cnt].dian=v;edge[cnt].zhi=w;edge[cnt].next=head[u];head[u]=cnt;edge[++cnt].dian=u;edge[cnt].zhi=w;edge[cnt].next=head[v];head[v]=cnt;
}
void spfa(int s){memset(vis,0,sizeof(vis));memset(dis,0x7f7f7f7f,sizeof(dis));queue<int> q;vis[s]=1;q.push(s);dis[s]=0;while(!q.empty()){int ck=q.front();q.pop();vis[ck]=0;for(int i=head[ck];i!=-1;i=edge[i].next){if(i&1) continue;if(dis[edge[i].dian]>dis[ck]+edge[i].zhi){dis[edge[i].dian]=dis[ck]+edge[i].zhi;if(!vis[edge[i].dian]){vis[edge[i].dian]=1;q.push(edge[i].dian);}}}}
}
void new1(){memset(is,0,sizeof(is));memset(in1,0,sizeof(in1));memset(in2,0,sizeof(in2));for(int u=1;u<=n;u++){for(int i=head[u];i!=-1;i=edge[i].next){if(i&1) continue;if(dis[u]+edge[i].zhi==dis[edge[i].dian]){is[i]=1;is[i^1]=1;in1[edge[i].dian]++;in2[u]++;}}}
}
void topo(int s){memset(cnt1,0,sizeof(cnt1));memset(cnt2,0,sizeof(cnt2));queue<int> q;q.push(s);cnt1[s]=1;while(!q.empty()){int u=q.front();q.pop();for(int i=head[u];i!=-1;i=edge[i].next){if(!is[i]||(i&1)) continue;int v=edge[i].dian;in1[v]--;cnt1[v]=(cnt1[v]+cnt1[u])%mod;if(!in1[v]) q.push(v);}}for(int i=1;i<=n;i++){if(!in2[i]){cnt2[i]=1;q.push(i);}}while(!q.empty()){int u=q.front();q.pop();for(int i=head[u];i!=-1;i=edge[i].next){if(!is[i]||!(i&1)) continue;int v=edge[i].dian;in2[v]--;cnt2[v]=(cnt2[v]+cnt2[u])%mod;if(!in2[v]){q.push(v);cnt2[v]++;//自己 }}}
}
void cal(){for(int u=1;u<=n;u++){for(int i=head[u];i!=-1;i=edge[i].next){if((i&1)||!is[i]) continue;int v=edge[i].dian;ans[i>>1]=(ans[i>>1]+cnt1[u]*cnt2[v]%mod)%mod;}}
}
void solve(){for(int i=1;i<=n;i++){spfa(i);new1();topo(i);cal();}for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
}
int main(){cin>>n>>m;memset(head,-1,sizeof(head));for(int i=1;i<=m;i++){scanf("%d%d%d",&u,&v,&w);add(u,v,w);}solve();return 0;
}2.最短路+DP
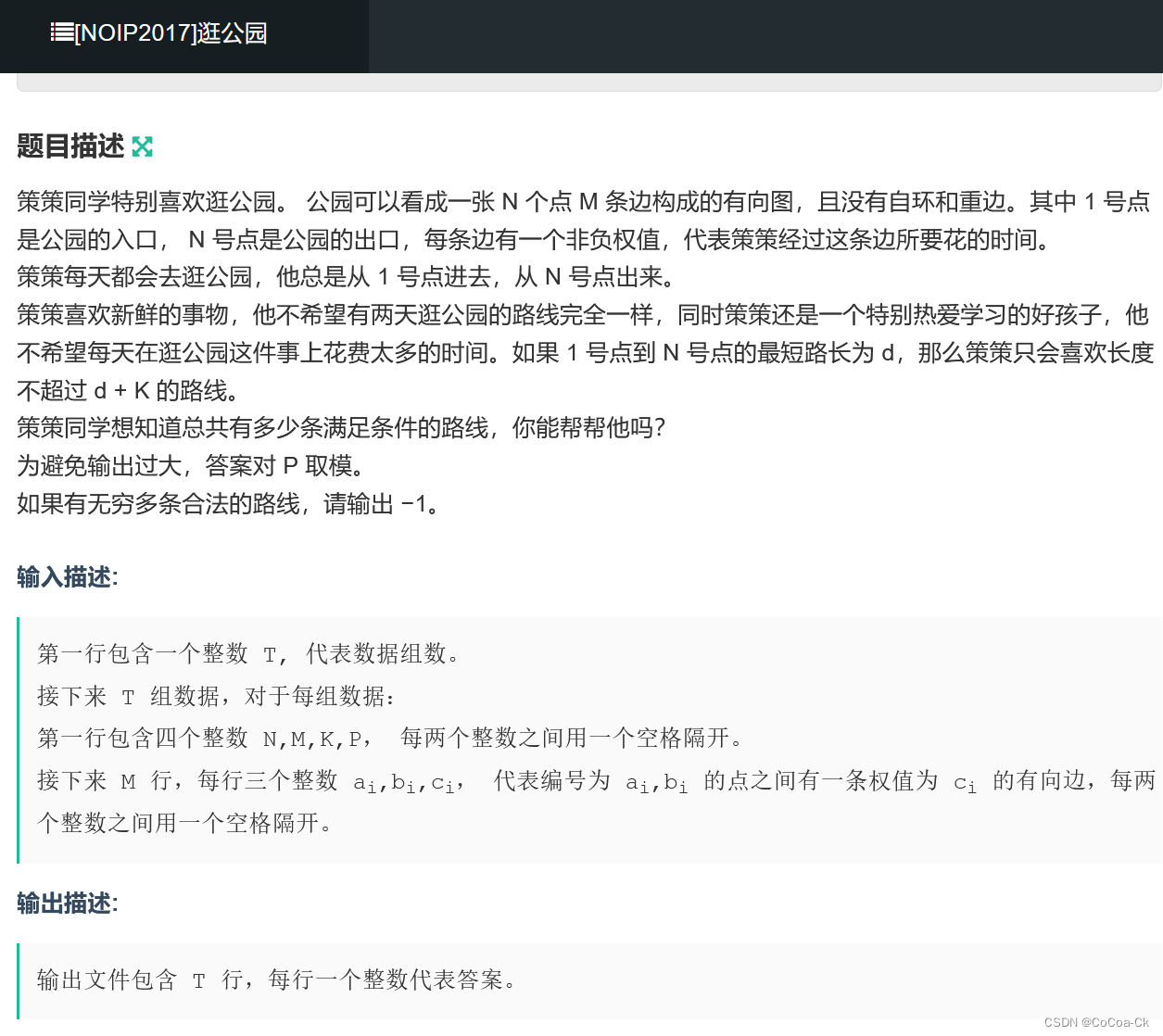
首先跑个最短路,然后我们令f[i][j]表示走到i不超过d+j的条数。
易得状态转移方程:f[x][k]=(f[y][dis[x]+k-dis[y]-len2[x][y])%p;
至于顺序我们直接记忆化搜素即可。
这里有个比较麻烦的细节:
如何判断0环?
1.不是一有0环就-1,当你的0环不在最短路+k涉及的路径上它起不了作用,那么这如何判?
注意到此时dis[x]+k-dis[y]-len2[x][y]为负值,我们判一下这种情况即可。
2.当一个二维位置即同一个点,同一个小于距离出现时,说明0环,判-1.
因此我们还要用v[n][55]来记录有没有访问过(注意dfs完后归0操作)
3.注意到0环涉及起点1的情况,这也是为什么起点设在n+1源点而不是1的原因。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=100000;
int t,n,m,k,p,a,b,c,flag;
vector<int> edge[N+1],len[N+1];
vector<int> edge1[N+1],len2[N+1];
int dis[N+1],vis[N+1];
int f[N+1][55];
bool v[N+1][55];
struct ty{int x,dis;bool operator< (const ty &a) const{return dis>a.dis;}
};
priority_queue<ty> q;
void dij(int s){memset(dis,0x7f,sizeof(dis));memset(vis,0,sizeof(vis));dis[s]=0;q.push({s,0});while(!q.empty()){ty tmp=q.top();q.pop();if(vis[tmp.x]) continue;vis[tmp.x]=1;for(int i=0;i<edge[tmp.x].size();i++){int y=edge[tmp.x][i];if(dis[y]>dis[tmp.x]+len[tmp.x][i]){dis[y]=dis[tmp.x]+len[tmp.x][i];q.push({y,dis[y]});}}}
}
int dfs(int x,int k){if(f[x][k]!=-1) return f[x][k];f[x][k]=0;v[x][k]=1;for(int i=0;i<edge1[x].size();i++){int y=edge1[x][i];int t=dis[x]+k-dis[y]-len2[x][i];if(t<0) continue;if(v[y][t]) flag=1;if(flag) return 0; f[x][k]=(f[x][k]+dfs(y,t))%p;}v[x][k]=0;return f[x][k];
}
int main(){cin>>t;while(t--){scanf("%d%d%d%d",&n,&m,&k,&p);for(int i=1;i<=n+1;i++){edge[i].clear();len[i].clear();edge1[i].clear();len2[i].clear();}for(int i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&c);edge[a].push_back(b);len[a].push_back(c);edge1[b].push_back(a);len2[b].push_back(c);}edge[n+1].push_back(1);len[n+1].push_back(0);edge1[1].push_back(n+1);len2[1].push_back(0);dij(n+1);memset(f,-1,sizeof(f));memset(v,0,sizeof(v));f[n+1][0]=1;int ans=0;flag=0;for(int i=0;i<=k;i++){ans=(ans+dfs(n,i))%p;}if(flag) printf("-1\n");else printf("%d\n",ans);}
}






![filebox在线文件管理工具V1.11.1.1查分吧修改自用版免费分享[PHP]](https://img-blog.csdnimg.cn/direct/510f10a56ec049929c13fbde48143224.png)