在学习单调队列或单调栈时，我们要先清楚，为何栈或队列是保持单增或单减，并且这样为何是有效的。比如保持单增，用单调队列的思想考虑的情况下，在遍历的过程中，我们需要解决的问题是寻找第一个比它小的（或者维护窗口中最小的元素），当前元素进队/栈时，如果栈顶或队尾存在比当前元素大的元素时，这些元素都是冗余的，因为当前元素在往后考虑时的作用 会一定更接近往后的元素且更小（更满足我们需要第一个小的要求）并且在单调队列中也更会留在窗口中。（单调栈有不同实现方式和思想，这里只描述了一种，详情请往下看）

一、单调栈

1.1、栈的思想

  栈是一种非常直观且广泛应用的数据结构，其主要特点是后进先出（LIFO，Last In, First Out）。想象一下一摞盘子或书籍，你只能从顶部添加或移除它们。栈可以临时存放一些数据，以便于之后逆序访问它，比如进制转换。
  浏览器的前后进是个很形象的例子：浏览器允许用户后退和前进浏览过的网页。这可以通过两个栈来实现：一个栈用于后退，另一个用于前进。当你访问新页面时，前进栈清空，当前页面压入后退栈。当你点击后退时，从后退栈中弹出，并将其压入前进栈。前进按钮则相反。

1.2、单调栈

  单调栈是一种特殊的栈，其元素按照单调递增或单调递减的顺序排列（根据特殊需求也可以是非减或非增序列）。单调栈用于解决那些需要寻找每个元素左侧或右侧第一个比它大（或小）的元素的问题。当新的元素被尝试加入栈时，会从栈顶开始移除破坏单调性的元素，直到保持栈的单调性为止，然后将新元素入栈。
应用示例：在一个数组中，为每个元素找出其右侧或左侧第一个更大的元素。LeetCode：柱状图中最大的矩形

如果要求的是左侧或右侧的最大/小值（而不是第一个更大/小的），可以用动态规划求解，如LeetCode：接雨水

1.2.1、单调栈的基本应用：找出数组中每个元素右侧第一个更大的元素

  使用单调栈解决这个问题的基本思路是遍历数组，对于每个元素，我们想找到它右侧第一个更大的元素。单调栈可以帮助我们追踪已经遍历过的元素，并保持它们的顺序，以便快速找到每个元素的答案。

• 初始化一个空栈，用于存放数组元素的索引。
• 遍历数组中的每个元素：
  • 当栈不为空且当前元素大于栈顶索引对应的元素时，表示找到了栈顶元素右侧的第一个更大元素。此时，将栈顶元素出栈，并记录当前元素为栈顶元素右侧第一个更大的元素。
  • 将当前元素的索引入栈。
• 对于栈中剩余的元素，它们右侧没有更大的元素。

#include <vector>
#include <stack>
using namespace std;class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums) {int n = nums.size();vector<int> ans(n, -1); // 初始化结果数组，假设每个元素的右侧没有更大的元素stack<int> myStack; // 用于存储索引，栈顶到栈底单调递减for (int i = 0; i < n; ++i) {// 当前元素大于栈顶元素对应的值时，说明找到了一个更大的元素while (!myStack.empty() && nums[i] > nums[myStack.top()]) {ans[myStack.top()] = nums[i]; // 更新栈顶元素的下一个更大元素myStack.pop(); // 弹出栈顶元素}// 将当前元素的索引入栈myStack.push(i);}// 对于栈中剩余的元素，它们的右侧没有更大的元素，ans中已经预设为-1，因此无需再操作return ans;}
};

1.2.2、单调栈的基本应用：找出数组中每个元素左侧第一个更大的元素

  可以直接使用1.2.1的方法反向扫描，反向扫描的右边实际上是原来的左边。如果在一个问题中同时求这俩，那用反向扫描肯定是最便捷的方式。 也可以直接从左往右扫描，如果栈顶元素比当前元素小则弹栈，直到遇到比当前元素大的则是左侧第一个更大元素。（这和单调队列的弹出队列的方式很像，因为比它小的不仅对以后没用，对当前元素来说也没用。）

#include <vector>
#include <stack>
using namespace std;class Solution {
public:vector<int> leftGreaterElement(vector<int>& nums) {int n = nums.size();vector<int> ans(n, -1); // 初始化结果数组，假设每个元素的左侧没有更大的元素stack<int> myStack; // 用于存储索引，栈顶到栈底单调递减for (int i = 0; i < n; ++i) {// 当前元素大于栈顶元素对应的值时，说明当前元素是遍历到目前为止的最大元素// 这里不需要像找右侧元素那样进行元素的更新，因为我们关心的是左侧元素while (!myStack.empty() && nums[i] >= nums[myStack.top()]) {myStack.pop(); // 弹出栈顶元素}// 如果栈不为空，说明找到了当前元素左侧的第一个更大元素if (!myStack.empty()) {ans[i] = nums[myStack.top()];}// 将当前元素的索引入栈myStack.push(i);}return ans;}
};

1.2.3、单调栈拓展

  单调栈的一次遍历不仅仅只能解决找到第一个更小的问题，它一次遍历就能找到左右两边的信息，不过有一边是等高的，有时候我们可以利用这一个特点来处理问题。这样的拓展使用需要在不同问题中发现，如1.2.4列出的题单。

for (int i = 0; i < n; ++i) {//递减序while (!myStack.empty() && nums[i] >= nums[myStack.top()]) {//右侧if(nums[i]>nums[myStack.top()]) 则能找到右侧更大，但可能出现相等的情况，可能相等的情况并不影响答案//所以需要有这种考虑和想法，以便于后面遇到这样的问题能够思考到，然后利用起来myStack.pop(); // 弹出栈顶元素}if (!myStack.empty()) {left_max[i] = nums[myStack.top()];//左边更大一定是正确的}myStack.push(i);
}

1.2.4、单调栈LeetCode题单

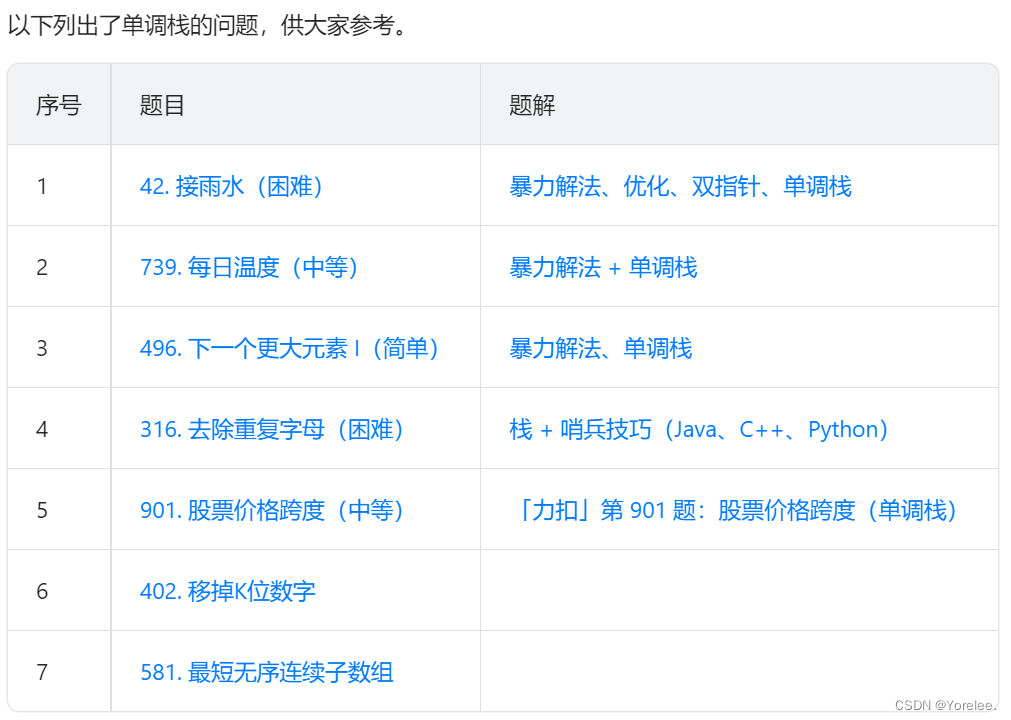
二、单调队列

2.1、队列的思想

  队列是一种先进先出（First In, First Out，FIFO）的数据结构，其工作原理类似于日常生活中的排队等待。在队列中，元素从一端（通常称为队尾）添加，从另一端（称为队头）进行移除。这种结构确保了元素被处理的顺序正是它们被添加到队列中的顺序，就像人们在商店结账处排队一样：先来的人先得到服务，新来的人排在队伍的末尾。

2.2、单调队列

  单调队列是一种特殊的队列，其元素同样按照单调递增或单调递减的顺序排列。不同于单调栈，单调队列支持在两端进行操作：在队列的一端添加元素，在另一端移除元素。这种结构适用于滑动窗口类的问题，其中窗口在数据序列上滑动，而我们希望快速获取窗口内的最大值或最小值。
应用示例：给定一个数组和一个窗口大小，为每个窗口找出最大值或最小值。

单调队列的应用：滑动窗口最大值

  单调队列解决的是另一个问题：给定一个数组和一个窗口大小，为每个窗口找出最大值。单调队列通过维护一个双端队列（Deque），其中保存可能成为当前窗口最大值的元素索引，确保队列是单调递减的。LeetCode求滑动窗口最大值

• 初始化一个空的双端队列（Deque）。
• 遍历数组中的每个元素：
  • 移除队列中所有小于当前元素的索引，因为它们不可能是包含当前元素的窗口的最大值。
  • 检查队头索引是否已经滑出窗口（即队头索引对应的元素不在当前考虑的窗口内），如果是，将其从队头移除。
  • 将当前元素的索引添加到队列尾部。
  • 对于每个窗口，队头索引总是对应该窗口的最大值。且队列里总是会有元素（因为至少当前正在遍历的元素一定在窗口中）。

#include <vector>
#include <deque>
using namespace std;class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {deque<int> myque; // 存储的是nums的索引，保证从大到小排列vector<int> ans;for(int i = 0; i < nums.size(); ++i) {// 如果队列不为空且当前元素大于等于队列最后一个元素所对应的值，则弹出队列最后一个元素while(!myque.empty() && nums[i] >= nums[myque.back()]) {myque.pop_back();}// 将当前元素索引加入队列myque.push_back(i);// 确保队列第一个元素始终在当前滑动窗口的范围内if(myque.front() <= i - k) {myque.pop_front();}// 当索引达到窗口大小-1时，开始记录结果if(i >= k - 1) {ans.push_back(nums[myque.front()]);}}return ans;}
};

三、单调栈和单调队列的区别

  你会发现单调队列和单调栈的区别在于，是否包含一个滑动窗口，单调队列处理的之前的成员可能会"失效"，但是单调栈的成员一直不会失效，因此单调队列有一个“失效”出队的操作。单调栈处理的问题中，一旦元素入栈，它们就保持有效，直到被明确地由一个满足特定条件的后来者替代；而单调队列处理的问题中，元素的有效性不仅受到队列中其他元素的影响，还受到它们是否仍然处于考虑的窗口内的影响。

示例解释

  假设你有一系列人的身高，你需要找到每个人右侧的第一个更高的人（单调栈），或者在一系列长度为k的连续子序列（即窗口）中找到最高的人（单调队列）。

• 单调栈：当一个新人加入时，如果他比前面的人都高，那么他就成为了前面某些人右侧第一个更高的人。前面比他矮的人都不再重要，因为他们已经找到了比自己高的人。
• 单调队列：对于每个长度为k的窗口，你想快速知道最高的人。当一个新人加入窗口时，如果他比窗口中的某些人高，那么这些比他矮的人就不可能是该窗口的最高者了。但是，窗口滑动时，最高的人可能会离开窗口，所以你需要记录下一个可能最高的人。

  通过使用单调栈和单调队列，你可以高效地解决这些问题，而不需要对每个元素或每个窗口进行独立的比较。每个元素进栈（队）一次，出栈（队）一次，因此时间复杂度均为O(n)。