一、并查集概念
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。
并查集的思想是用一个数组表示了整片森林(parent),树的根节点唯一标识了一个集合,我们只要找到了某个元素的的树根,就能确定它在哪个集合里。
【摘自菜鸟教程】
只看上面这段例子可能会发懵,让我们来看一个详细的例子。
大家看剧都知道,古时候基本上都会拉帮结派,形成大大小小许多帮派。这些帮派都会有等级划分,大当家,二当家,等等。类似于这样的结构。

假如三当家的小弟想知道他真正的老大是谁,那么他就去问三当家,三当家就告诉他他的老大是二当家,然后这个小弟就去问二当家,二当家就会告诉他,他的老大是大当家,那么小弟再去问大当家,大当家就会告诉他,我才是你真正的老大。那么所有这些人,他们的老大都只有一个,那就是“大当家”。
翻译成大白话说就是:如果一个元素的老大不是他自己,那么他自己的老大的老大就是他的老大。
这就是小弟找老大的过程,也就是“并查集”中“查”的部分。
假如突然有一天,大当家干掉了自己的死对头(另一个帮派的老大)并成功吞并了他的帮派。

那么现在,另一个帮派的小弟再找大哥时,就会发现,此时自己的大哥已经变成了另一个帮派的大哥。这就是“并查集”中“并”的部分。
二、并查集在算法题中应用
接下来我们根据一道算法题来看一下如何使用并查集。
Leetcode 547. 省份数量
题目描述
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:
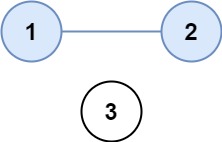
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]] 输出:2
示例 2:

输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]] 输出:3
提示:
1 <= n <= 200n == isConnected.lengthn == isConnected[i].lengthisConnected[i][j]为1或0isConnected[i][i] == 1isConnected[i][j] == isConnected[j][i]
简单分析题目后发现,这就是一个找大哥的过程。每一个省份算作一个帮派,有几个“大哥”就是有几个省份,所以该题可以使用并查集。
直接上代码:
class Solution {public int findCircleNum(int[][] isConnected) {// 定义一个新数组用来记录每个城市的大哥int[] city = new int [isConnected.length];// 初始化数组,刚开始每个人的大哥都是自己for (int i = 0; i < city.length; i++) {city[i] = i;}// 遍历城市数组for (int i = 0; i < isConnected.length; i++) {for (int j = 0; j < isConnected[0].length; j++) {// 如果时同一个城市或者两个城市不相连,那么直接继续if (i == j || isConnected[i][j] == 0) {continue;}// “并”的过程,i城市的大哥就是j城市的大哥city[find(i, city)] = find(j, city);}}// 遍历 city 数组,看看有几个大哥int res = 0;for (int i = 0; i < city.length; i++) {if (i == city[i]) {res++;}}return res;}/*** “查”的过程,查找x城市的大哥** @param x 要找大哥的城市* @param city 定义每个城市的大哥的数组* @return x城市的大哥*/public int find(int x, int[] city) {// 如果 x 的大哥不是 x,那么就去找 x 大哥的大哥while (city[x] != x) {x = city[x];}return x;}
}