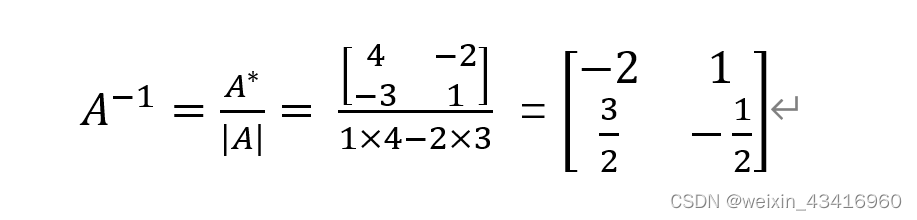文章目录
- 【numpy.exp()】返回e的幂次方,e是一个常数为2.71828
- 【np.dot()】矩阵相乘
- 【np.linalg.inv()】矩阵求逆
【numpy.exp()】返回e的幂次方,e是一个常数为2.71828
举例:numpy.exp()
【np.dot()】矩阵相乘
【要点】
1、前者的列数=后者的行数—>才能相乘
2、前者的行数、后者的列数–>结果矩阵
3、前者第一行,与后者所有列分别计算,得到结果第一行。
前者第二行,与后者所有列分别计算,得到结果第二行。
【计算示例】

计算过程:

【np.linalg.inv()】矩阵求逆
【要点&例举】
1、矩阵的逆:等于伴随矩阵除以行列式
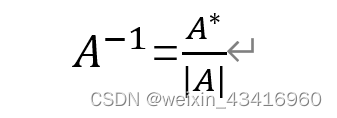
2、伴随矩阵:主交换,副变号
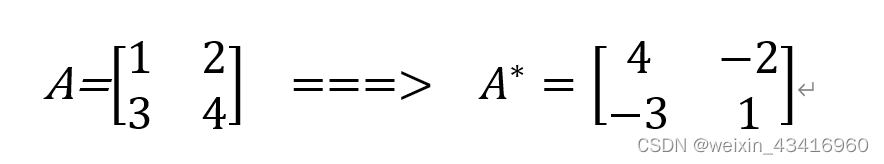
3、行列式:主相乘-副相乘
|A| = 1×4-2×3=-2
4、结果: