摘要

本周阅读了一篇基于时间与非时间序列模型耦合来模拟城市内涝区洪水水深的文章，文中提出了一种极值梯度提升和长短记忆算法的耦合模型。通过对郑州市三个典型的洪水点的实际应用，结果表明，该耦合模型能较好地拟合和预报洪水。验证数据的平均相对误差、Nash-Sutcliffe效率系数和合格率的平均值分别为9.13%、0.96和90.3%。此外，还对文中用到的Boosting算法的相关内容进行补充学习，Boosting是有关提升、增强的算法。

Abstract

This week, an article on simulating flood depth in urban waterlogging areas based on the coupling of time and non time series models is readed. A coupled model of extreme gradient enhancement and long short-term memory algorithm is proposed in the article. Through the practical application of three typical flood points in Zhengzhou City, the results show that the coupled model can fit and predict floods well. The average relative error, Nash Sutcliffe efficiency coefficient, and pass rate of the validation data are 9.13%, 0.96%, and 90.3%, respectively. In addition, supplementary learning is conducted on the relevant content of Boosting algorithm used in the article, which is an algorithm related to enhancement and enhancement.

文献阅读

题目

Coupling Time and Non‑Time Series Models to Simulate the Flood Depth at Urban Flooded Area

创新点

本研究将XGBoost回归模型与LSTM回归模型耦合，对郑州市部分洪泛区的洪水埋深进行了预测。
具体如下：
（1）将洪水的突变过程分为雨期和雨后两个阶段；
（2）利用降雨资料，建立非时间序列回归模型，利用XGBoost算法预测雨期洪水的水深;
（3）基于XGBoost回归模型预测的数据，将LSTM算法应用于时间序列模型，预测雨后洪水的洪水深度;
（4）利用XGBoost和LSTM算法耦合模型预测不同重现期降雨淹没区的洪水深度。

实验数据

研究区域

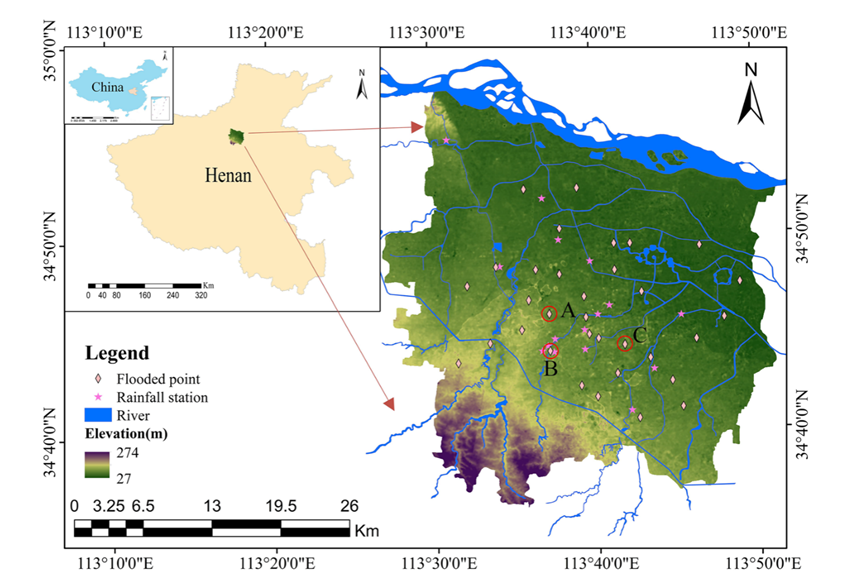
郑州地理位置所导致的大陆性季风气候（Lv et al. 2021），尽管年降雨量达到640.9 mm，但60%的降水集中在夏季，这导致郑州市城市洪水风险增加。

自数据记录开始以来，有些地区被洪水淹没的频率很高，选择A点、B点和C点作为本次研究的重点水淹区。

数据和材料

本研究将降雨量的相关数据作为预测变量输入模型，将各点的洪水深数据作为模型的输出变量。所需数据的详细说明如下：
1.雨量数据：降雨量数据为郑州市16个雨量观测站在历史降雨事件下的自记雨量计观测到的降雨量时间序列数据。数据来自河南省气象局。
2.泛洪数据：洪水数据包括城市灾害数据库中存储的城市淹没区域的位置和深度信息，这些信息是从每个交叉口的监测设备收集的。这些监测设备由郑州市城市管理局管理。

方法

XGBoost algorithm

XGBoost算法由多个相关的CART树共同决定，因此下一个决策树的输入样本将与前一个决策树的训练和预测结果相关：

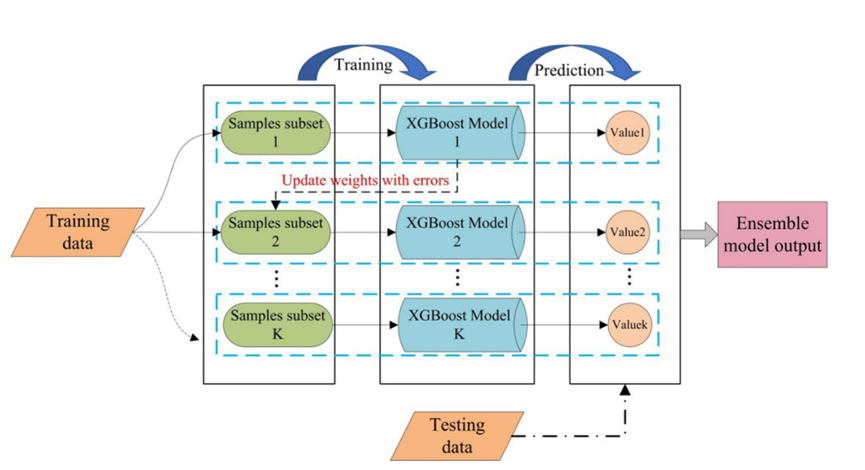
XGBoost算法是一种用于大规模并行化的提升树集成，是目前最快和最好的集成决策树算法。XGBoost算法原理的推导过程如下：

Long Short‑Term Memory Algorithm

LSTM算法与大多数神经网络具有相同的结构，即输入层，隐藏层和输出层。LSTM中隐藏层的单元是线性自循环记忆块，包含自连接记忆单元的记忆块可以记忆时间状态（如下图）。依靠三个门（输入门it、输出门ot和遗忘门ft）来控制信息流入和流出：

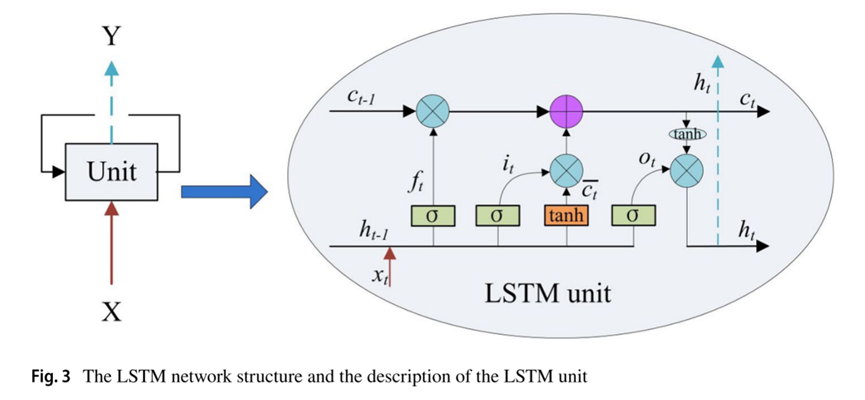
任何时间t的输入特征由输入xt和先前的隐藏状态ht-1通过tanh函数计算：

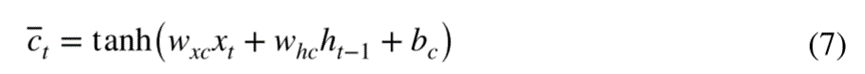
输入特征和先前存储器单元的部分遗忘用于更新存储器单元，并且隐藏输出状态ht最终由输出门ot和存储器ct计算：

LSTM网络yt的输出可以表示为：

Evaluation of the Model Accuracy

选择平均相对误差、Nash-Sutcliffe效率系数和合格率（MRE、NSE和QR）（表1）作为模型的定量评价指标：

实验结果

为了验证模型的有效性，将LSTM模型与XGBoost回归模型进行比较，将相同的数据应用于XGBoost模型和LSTM模型。如表所示，经验证的三个降雨事件的LSTM和XGBoost模型得到的平均NSE分别为0.90和0.86。LSTM模型的MRE值较低，表明LSTM模型对雨后期城市洪水深度的预测精度更高。

对3次降雨事件的模拟结果进行分析，降雨期间XGBoost模型、降雨后LSTM模型和XGBoost与LSTM模型耦合模型模拟的洪水深度平均误差分别为8.87%、9.77%和9.13%，满足洪水预测的要求。同时，利用NSE和QR来评价模型的效率和精度。耦合模型的平均NSE为0.96，平均预测合格率为90.3%。结果表明，XGBoost与LSTM算法的耦合模型在洪水预报中是有效可行。

为了评估模拟值与实测值的差异，通过间隔10 min的系统采样生成拟合曲线如右图，结果表明，耦合模型预测值与实测值具有较强的一致性：

深度学习

XGBoost代码实现

XGBoost 的设计目标是高效、灵活、便携，在分类、回归和排名等各种任务中的表现优于其他机器学习算法。作为对 GBM 算法的改进，XGBoost 使用的正则化模型有助于防止过拟合，也有许多可调整的参数能提高算法的性能：
• max_depth：决策树的最大深度
• eta：学习率
• gamma：进行拆分所需的最小损失减少
• subsample：用于训练每棵树的训练数据的一部分

#import libraries
import pandas as pd
import numpy as np
from xgboost import XGBClassifier#read in data
df = pd.read csv ( 'data.csv ' )#split data into x and y
x =df.drop ( 'label', axis=1)
y = df [ 'label']
#fit model no training data
model = XGBClassifier ()
model.fit(X, y)

AdaBoost

Boosting是一种常用的统计学习方法，在分类问题中，通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。
以下介绍Boosting的思路和代表性的Boosting算法AdaBoost。

Boosting

Boosting思想：对于一个复杂任务来说，将多个专家的判断进行适当的综合所得出的判断要比其中任何一个专家单独的判断好。在概率近似正确学习的框架中，强可学习和弱可学习被证明是等价的。Boost所做的工作即是把弱可学习提升为强可学习算法。

Boosting的两个基本问题和答案：
一是在每一轮中如何改变训练数据的权值或概率分布；二是如何将弱分类器合成为强分类器。
第一个问题的答案是提高前一轮弱分类器错误分类样本的权值，降低那些被正确分类样本的权值。
第二个问题的答案，例如AdaBoost采取加权多数表决的方法。

AdaBoost算法

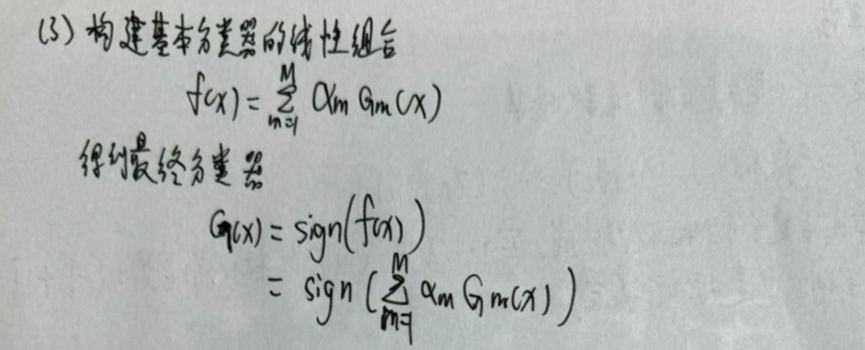
对AdaBoost算法作如下说明：
步骤（1） 假设训练数据集具有均匀的权值分布，即每个训练样本在基本分类器的学习中作用相同，这一假设保证第1步能够在原始数据上学习基本分类器G1（x）。

步骤（2） AdaBoost反复学习基本分类器，在每一轮m=1,2,…，M顺次执行下列操作：
（a） 使用当前分布Dm加权的训练数据集，学习基本分类器Gm（x）。
（b） 计算基本分类器Gm（x）在加权训练数据集上的分类误差率：

（c） 计算基本分类器Gm（x）的系数αm，αm表示Gm（x）在最终分类器中的重要性。
（d） 更新训练数据的权值分布为下一轮做准备。

步骤（3） 线性组合f（x）实现M个基本分类器的加权表决。系数αm表示基本分类器Gm（x）的重要性，这里，所有αm之和并不为1。利用基本分类器的线性组合构建最终分类器是AdaBoost的一大特点。

AdaBoost代码实现

def adaBoostTrainDS(dataArr,classLabels,numIt=40):"""基于单层决策树的AdaBoost训练过程:param dataArr: 数据集:param classLabels: 标签:param numIt: 迭代次数:return:多个弱分类器，包含其对应的alpha值"""weakClassArr = [] # 单层决策树数组m = shape(dataArr)[0]# D为每个数据点的权重，每个数据点的权重都会被初始化为1/mD = mat(ones((m,1))/m)aggClassEst = mat(zeros((m,1)))  # 记录每个数据点的类别估计累计值for i in range(numIt):# 构建一个最佳单层决策树bestStump,error,classEst = buildStump(dataArr,classLabels,D)print("D: ",D.T)# max(error,1e-16)))用于确保在没有错误时不会发生除零溢出# alpha:本次单层决策树输出结果的权重alpha = float(0.5*log((1.0-error)/max(error,1e-16)))  # 计算alphabestStump['alpha'] = alphaweakClassArr.append(bestStump) # 将最佳单层决策树存储到单层决策树数组中print("classEst: ",classEst.T)# 更新数据样本权值Dexpon = multiply(-1*alpha*mat(classLabels).T,classEst)D = multiply(D,exp(expon))D = D/D.sum()# 更新累计类别估计值aggClassEst +=alpha*classEstprint ("aggClassEst: ",aggClassEst.T)# 计算错误率aggErrors = multiply(sign(aggClassEst)!= mat(classLabels).T,ones((m,1)))errorRate = aggErrors.sum()/mprint ("total error: ",errorRate)# 如果错误率为0.0，则退出循环if errorRate==0.0:break
return weakClassArrdataMat,classLabels = loadSimpData()
D = mat(ones((5,1))/5)
classifierArr = adaBoostTrainDS(dataMat,classLabels,9)
print("classifierArr:\n",classifierArr)

运行结果如下：

测试算法：基于AdaBoost的分类：

def adaClassify(datToClass,classifierArr):"""利用训练出的多个弱分类器，在测试集上进行分类预测:param datToClass:一个或多个待分类样例:param classifierArr:多个弱分类器组成的数组:return:预测的类别值"""dataMatrix = mat(datToClass)m = shape(dataMatrix)[0]aggClassEst = mat(zeros((m,1)))  # 类别估计值for i in range(len(classifierArr)):  # 遍历每个分类器# 对每个分类器得到一个类别估计值classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],classifierArr[i]['thresh'],classifierArr[i]['ineq'])aggClassEst += classifierArr[i]['alpha']*classEstprint (aggClassEst)
return sign(aggClassEst) # 如果aggClassEst>0,则返回1，如果aggClassEst<=0,则返回-1dataMat,classLabels = loadSimpData()
D = mat(ones((5,1))/5)
classifierArr = adaBoostTrainDS(dataMat,classLabels,9)  # 得到弱分类器数组
print("预测[0,0]的类别结果:\n",adaClassify([0,0],classifierArr))
print("预测[[5,5],[0, 0]]的类别结果:\n",adaClassify([[5,5],[0, 0]], classifierArr))

运行结果如下：

总结

在一些问题中，AdaBoost方法相对于大多数其它学习算法而言，不会很容易出现过拟合现象。AdaBoost方法是一种迭代算法，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率。但是AdaBoost方法对于噪声数据和异常数据很敏感，这是其一大缺点。