62.不同路径

思路： 本题非常巧妙。
第一步：定义一个dp数组存储到达每个位置的路径数。
第二步：每个位置的路径数=它左面位置的路径数+上面位置的路径数。
第三步：不好想的是如何初始化数组。
既然只能向下或向右走，可推出最上面一排和最左面一列的所有位置上的路径只有一条。
第四步：遍历顺序是从右上角到左下角。
第五步：模拟一遍。

class Solution {public int uniquePaths(int m, int n) {int[][] dp=new int[m][n];//第一步：定义一个数组，表示到达该位置的路径数//3、初始化数组if(m==1 || n==1) return 1;for(int i=1;i<m;i++){dp[i][0]=1;}for(int i=1;i<n;i++){dp[0][i]=1;}for(int i=1;i<m;i++){//2、遍历顺序for(int j=1;j<n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];//4、递推公式}}return dp[m-1][n-1];//5、举例推导}
}

时间复杂度：O(m × n)
空间复杂度：O(m × n)

63. 不同路径 II

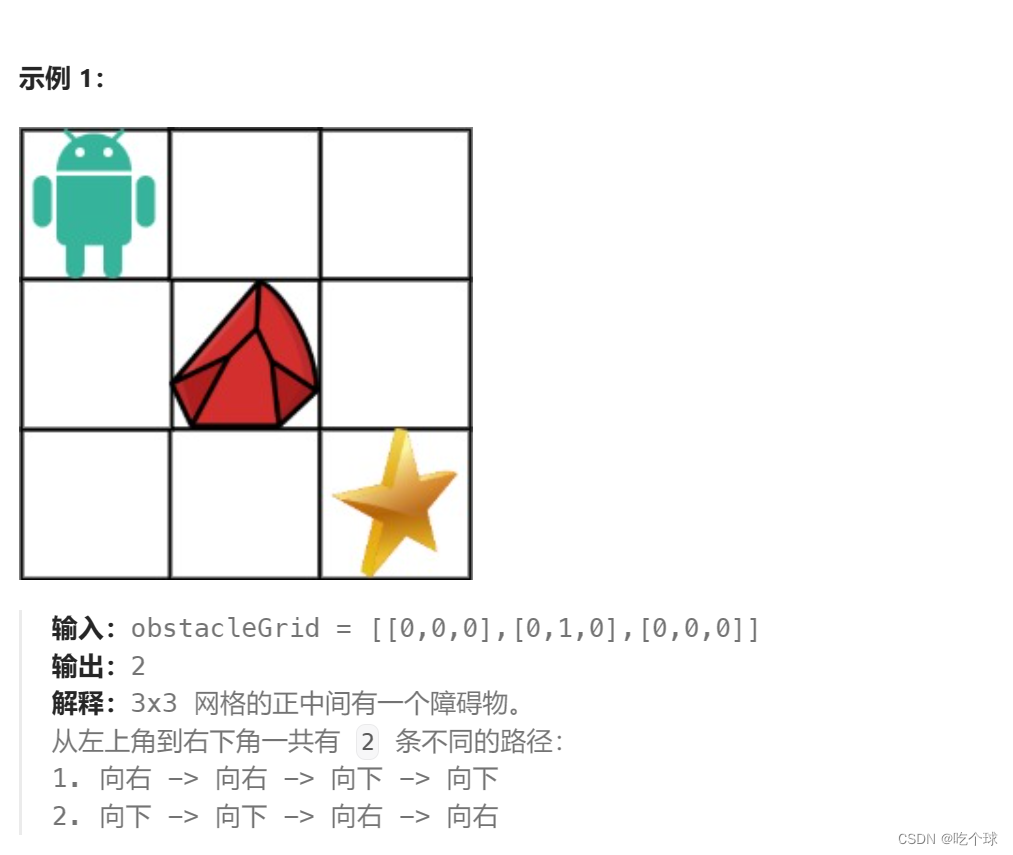
思路： 和上一题思路一样，只是遇到障碍物就将当前位置设为零。注意：当在初始化时遇到障碍物，则将之后的位置都设为0，因为根本无法到达这些位置。

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m=obstacleGrid.length;int n=obstacleGrid[0].length;int[][] dp=new int[m][n];for(int i=0;i<m;i++){if(obstacleGrid[i][0]==0) dp[i][0]=1;else break;}for(int i=0;i<n;i++){if(obstacleGrid[0][i]==0) dp[0][i]=1;else break;}for(int i=1;i<m;i++){for(int j=1;j<n;j++){if(obstacleGrid[i][j]==0){dp[i][j]=dp[i-1][j]+dp[i][j-1];}else{dp[i][j]=0;}}}return dp[m-1][n-1];}
}

时间复杂度：O(m × n)
空间复杂度：O(m × n)