1.俾斯麦海之战
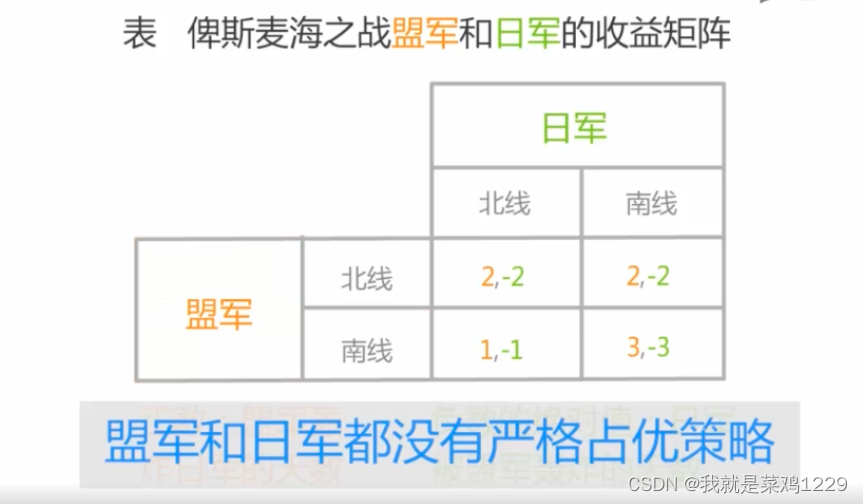
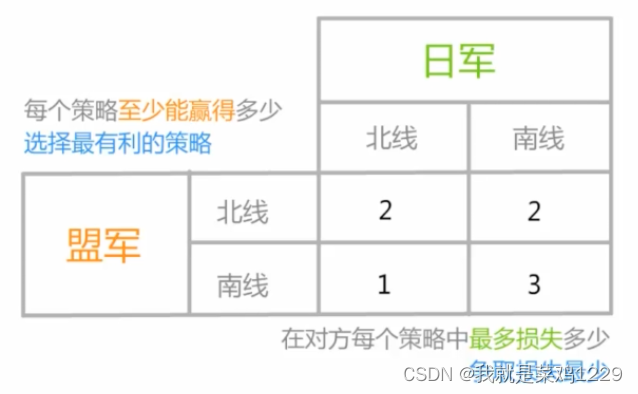
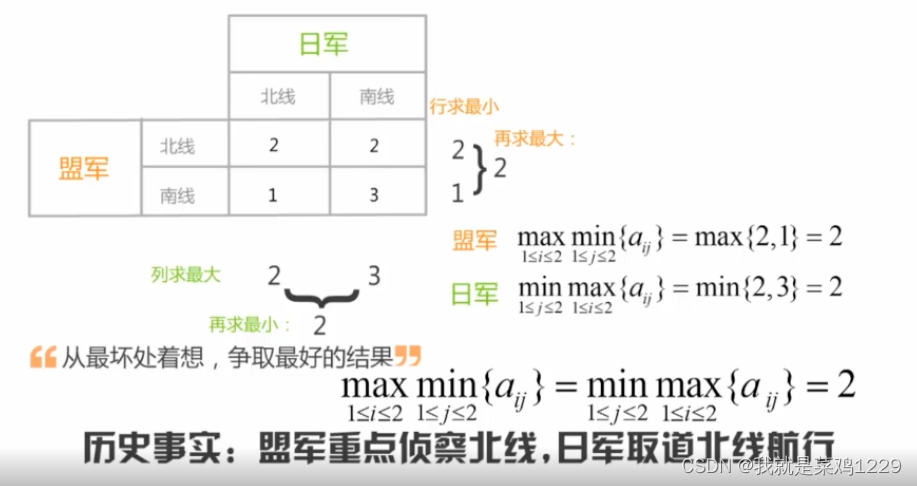
2. 零和博弈的定义
零和博弈(Zero-Sum Game)是一种博弈论的基本概念,指的是在博弈过程中,博弈参与者之间的收益和损失之和总是一个常数,特别是总和为零。即博弈一方的收益必然等于另一方的损失,不存在共赢或多赢的情况。换句话说,在零和博弈中,博弈双方的利益是对立的,博弈的结果是一方得利必定伴随着另一方的损失,整个博弈的总体价值是恒定不变的。
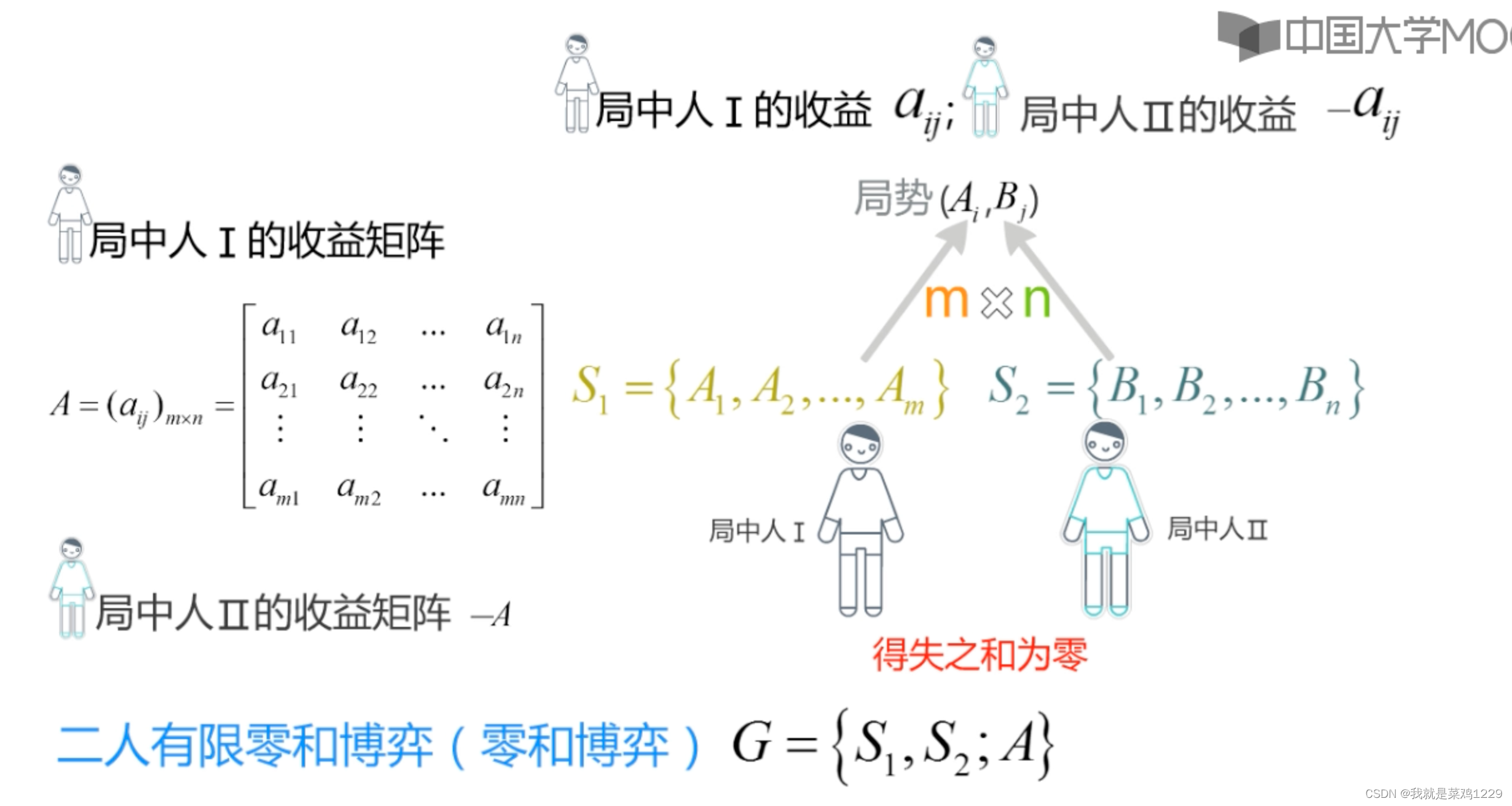
3. 纯策略纳什均衡
假设零和博弈 G = { S 1 , S 2 ; A } G=\{S_1,S_2;A\} G={S1,S2;A},其中 S 1 = { A 1 , A 2 . A 3 } S_1=\{A_1,A_2.A_3\} S1={A1,A2.A3}, S 2 = { B 1 , B 2 . B 3 } S_2=\{B_1,B_2.B_3\} S2={B1,B2.B3},
A = [ 6 − 1 0 3 1 2 − 3 0 − 1 ] A=\begin{bmatrix} 6 & -1 & 0 \\ 3 & 1 & 2 \\ -3 & 0 & -1 \end{bmatrix} A= 63−3−11002−1
各局中人应如何选择自己的策略,保证自己在博弈中取得有利的地位。



4.博弈论中的最小最大定理

对于任意一个两个玩家A和B之间的完全信息、零和、有限策略集的博弈,存在一个数V和玩家A的一个策略σ*,使得无论对手B采取何种策略,通过执行σ*,A所能获得的最小收益至少是V。同时,存在玩家B的一个策略τ*,使得当B执行τ*时,即使面对A的最优策略,其给A带来的最大损失也不超过V。
换句话说,A的最小期望得益(即最大损失)等于B的最大期望损失(即最小得益),这个相同的数值就是游戏的值V。A的最优策略是在所有可能的策略中找到那个能够抵御对手任何反击的策略,以确保最坏情况下的最好结果;而B则反过来尝试最大化A的最坏结果,即最小化自己的最大损失。
博弈在纯策略意义下的纳什均衡可以不唯一,博弈的值是唯一的。
5. 混合策略纳什均衡
假设零和博弈 G = { S 1 , S 2 ; A } G=\{S_1,S_2;A\} G={S1,S2;A},
其中 S 1 = { A 1 , A 2 , . . . A m } S_1=\{A_1,A_2,...A_m\} S1={A1,A2,...Am},选择每个策略的概率为 X = { x 1 , x 2 , . . . , x m } X=\{x_1,x_2,...,x_m\} X={x1,x2,...,xm};
S 2 = { B 1 , B 2 , . . . , B n } S_2=\{B_1,B_2,...,B_n\} S2={B1,B2,...,Bn},选择每个策略的概率为 Y = { y 1 , y 2 , . . . , y n } Y=\{y_1,y_2,...,y_n\} Y={y1,y2,...,yn}
A = ( a i j ) m × n A=(a_{ij})_{m\times n} A=(aij)m×n
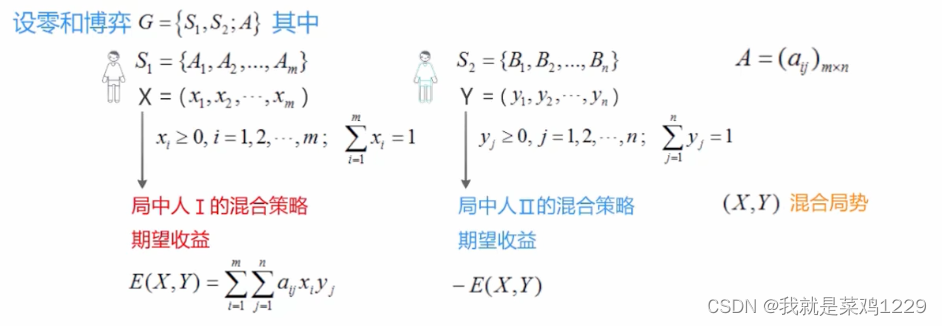
对于给定的博弈G,
局中人1的所有混合策略构成的集合 S 1 ∗ = { X } S_1^*=\{X\} S1∗={X}
局中人2的所有混合策略构成的集合 S 2 ∗ = { Y } S_2^*=\{Y\} S2∗={Y}
期望为 G ∗ = { S 1 ∗ , S 2 ∗ ; E } G^*=\{S_1^*,S_2^*;E\} G∗={S1∗,S2∗;E},为博弈G的混合扩充。
目标:

任何一个给定的二人零和博弈G一定存在混合策略意义下的纳什均衡
6.一个例子

7.非零和博弈的定义
- 各方的收益或损失的总和不是零值。
- 局中人之间不再是完全对立
- 一个局中人的所得并不一定意味着其他局中人要同样数量的损失
- 博弈参与方之间可能存在某种共同利益,可以“双赢”或“多赢”
7.1 求解二人非零和博弈混合策略纳什均衡的一般方法
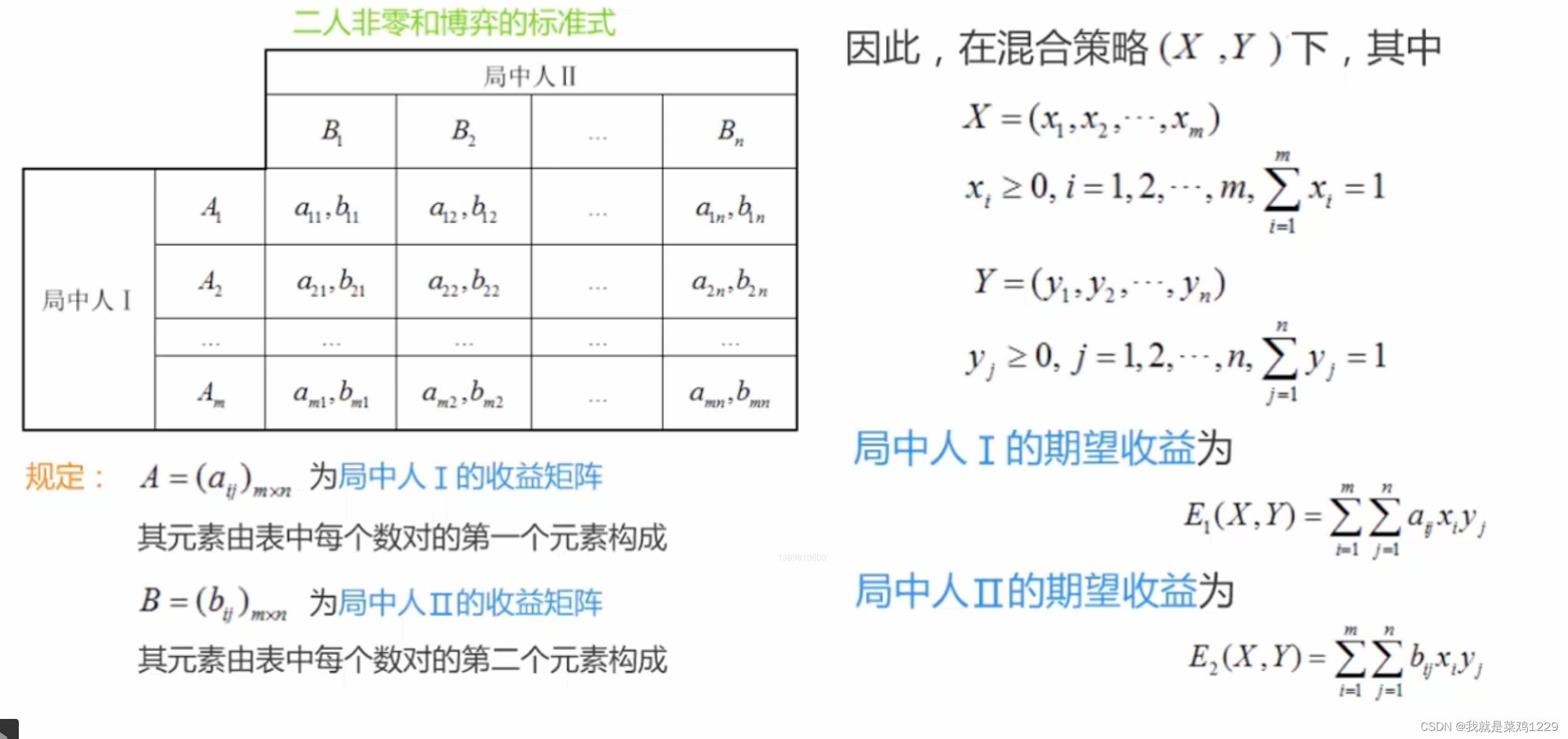
7.2 反复剔除严格劣策略
在“局中人是理性的”假设前提下,如果一个人的策略集合中存在严格劣策略,理性的他永远不会选择严格劣策略。反复剔除严格劣策略适用于零和博弈与非零和博弈。
- 对于局中人1的b策略严格劣与策略d,所以策略b可以删除。
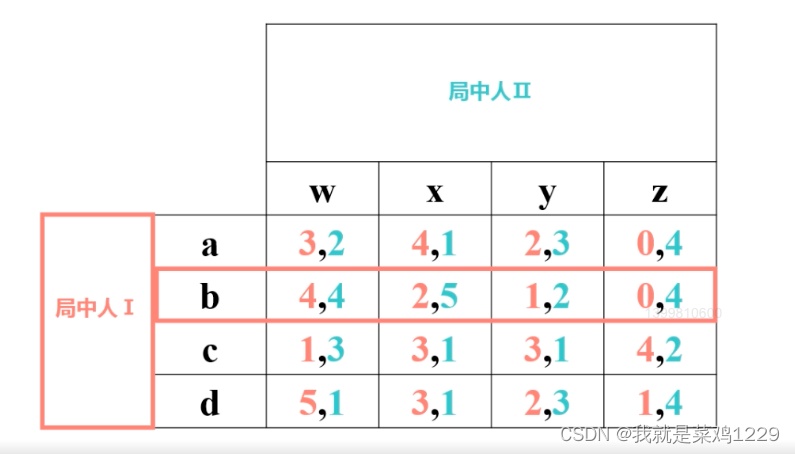
- 最后可以得到
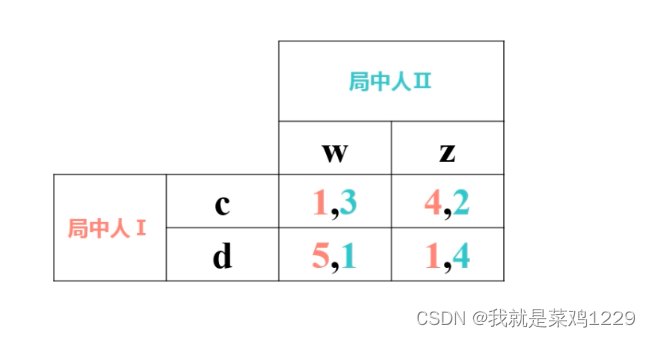
8.奇数定理及其应用
奇数定理:几乎所有的有限策略的博弈都有奇数个纳什均衡,包括纯策略纳什均衡和混合策略纳什均衡
简单来说,根据奇数定理,如果一个博弈有两个纯策略纳什均衡,则必定存在至少一个额外的纳什均衡,这导致了纳什均衡的总数是奇数。纳什均衡是指在一个博弈中,没有一个参与者可以通过单独改变自己的策略来改善其结果的稳定策略组合。
需要注意的是,“几乎所有的”这一描述表明并非所有博弈都严格遵循这个规律,但大部分有限博弈确实表现出这样的特性。这个定理对于理解和分析博弈论中的复杂交互行为有着重要意义。