计算机网络：物理层

计算机网络：物理层 - 信道复用

- 频分复用
- 时分复用
- 统计时分复用
- 波分复用
- 码分复用

计算机网络中，用户之间通过信道进行通信，但是信道是有限的，想要提高网络的效率，就需要提高信道的利用效率。因此计算机网络中普遍采用信道复用技术，让一条信道可以同时为多个用户服务。

复用是指多个用户使用一个共享信道进行通信

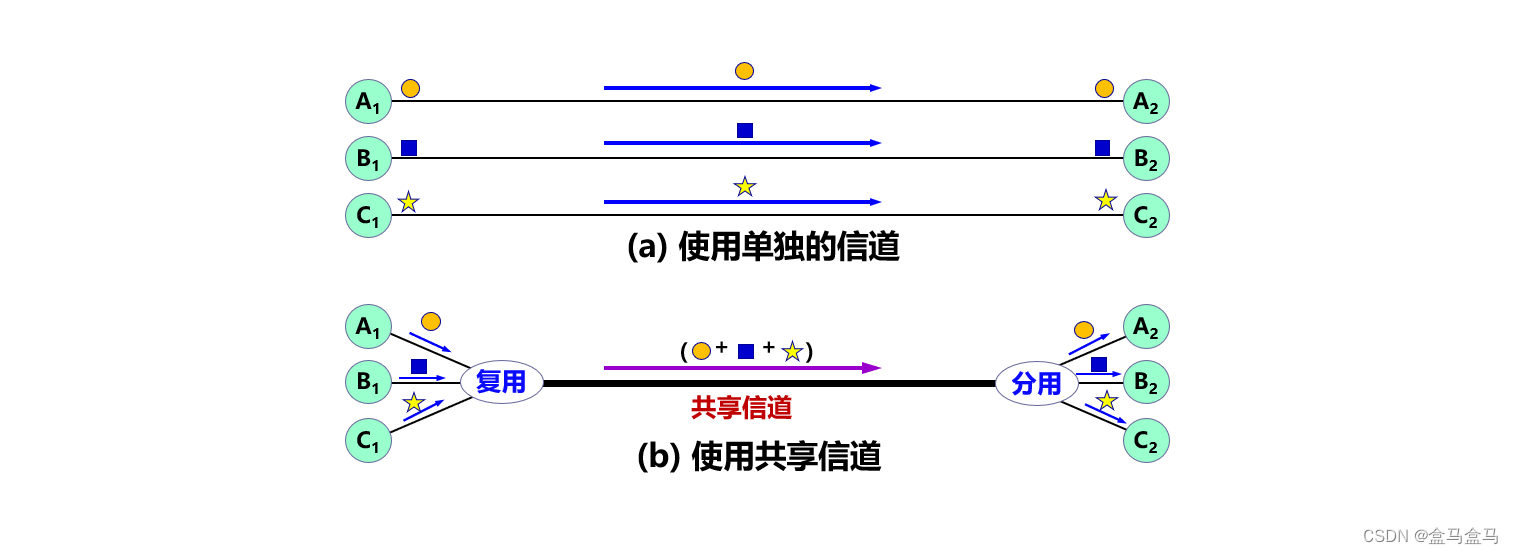
在这里插入图片描述

计算机网络中常见的信道复用技术有：频分复用，时分复用，统计时分复用，波分复用，码分复用。

频分复用

频分复用就是将用于传输信道的总带宽划分成若干个子频带（或称子信道），每一个子信道传输一路信号。用户在分配到一定的频带后，在通信过程中自始至终都占用这个频带。

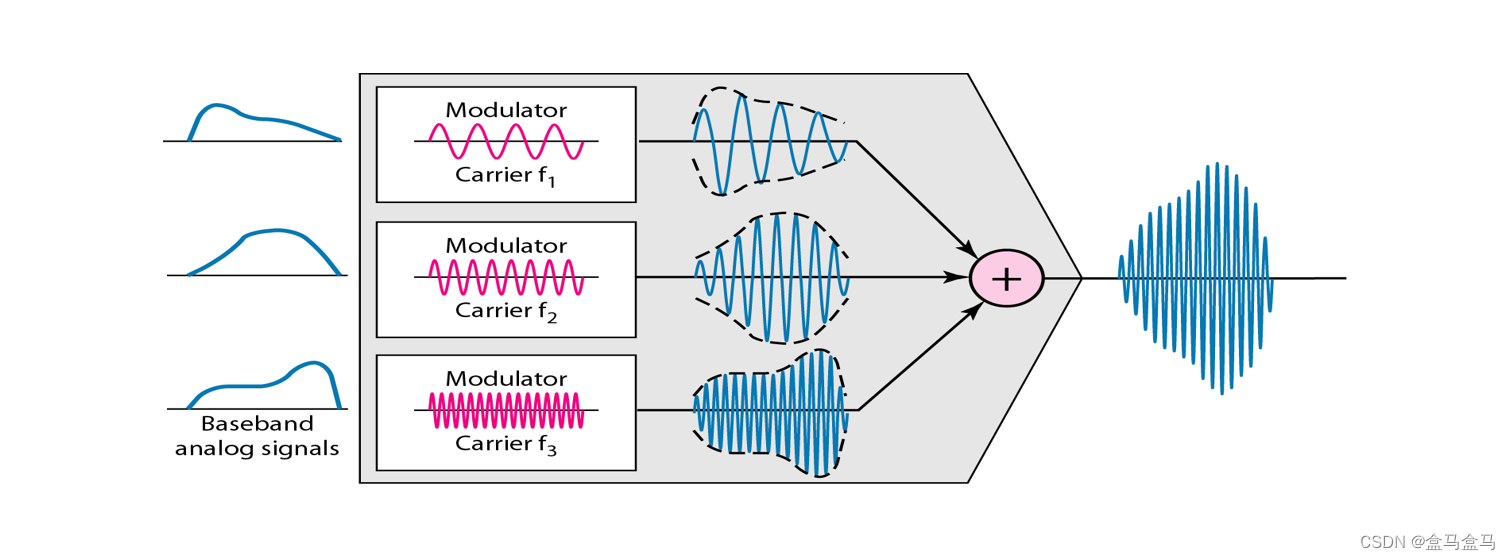
在这里插入图片描述

比如下图：

在这里插入图片描述

左侧是三段不同的信号，经过Modulator即调制器，把三段信号用不同的方式调制，调制到不同的频率，再把调制后的三段信号混合传输出去。由于调制后的三段信号占用的频率是不同的，所以可以把三段不同频率的信号拆分出来，就得到了三条独立的信号：
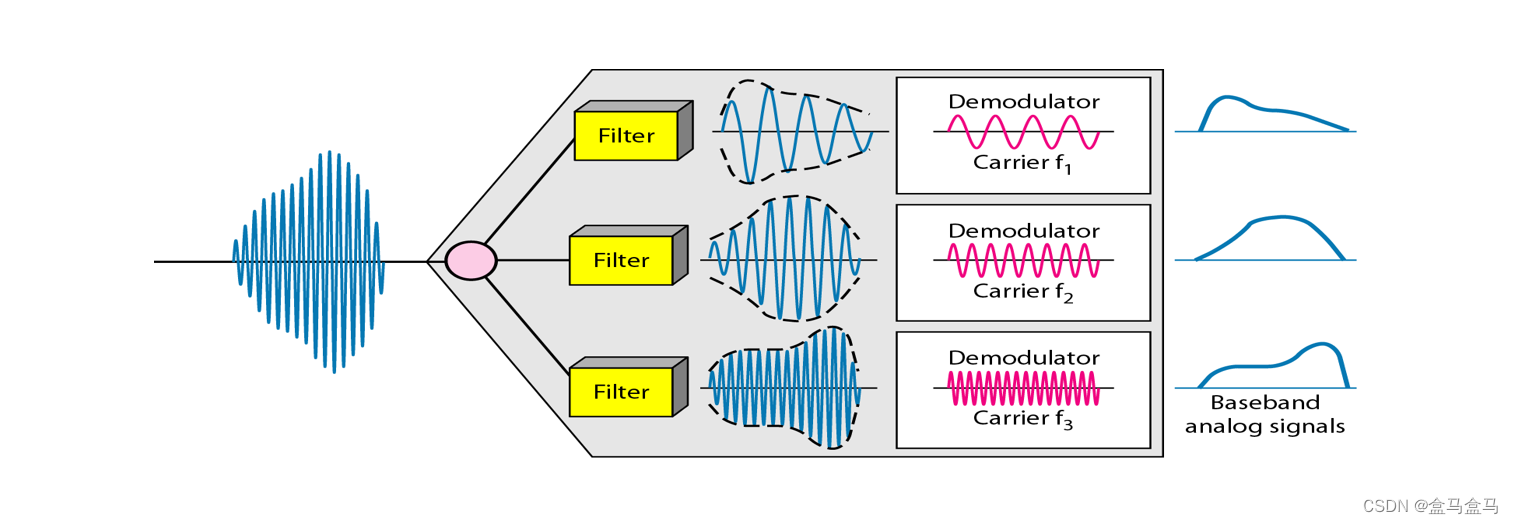
在这里插入图片描述

拆分后的不同信号，再经过对于的Demodulator解调器，就可以还原出最原始的信号。这就是频分复用的基本原理。

再看到一个量化的例子：
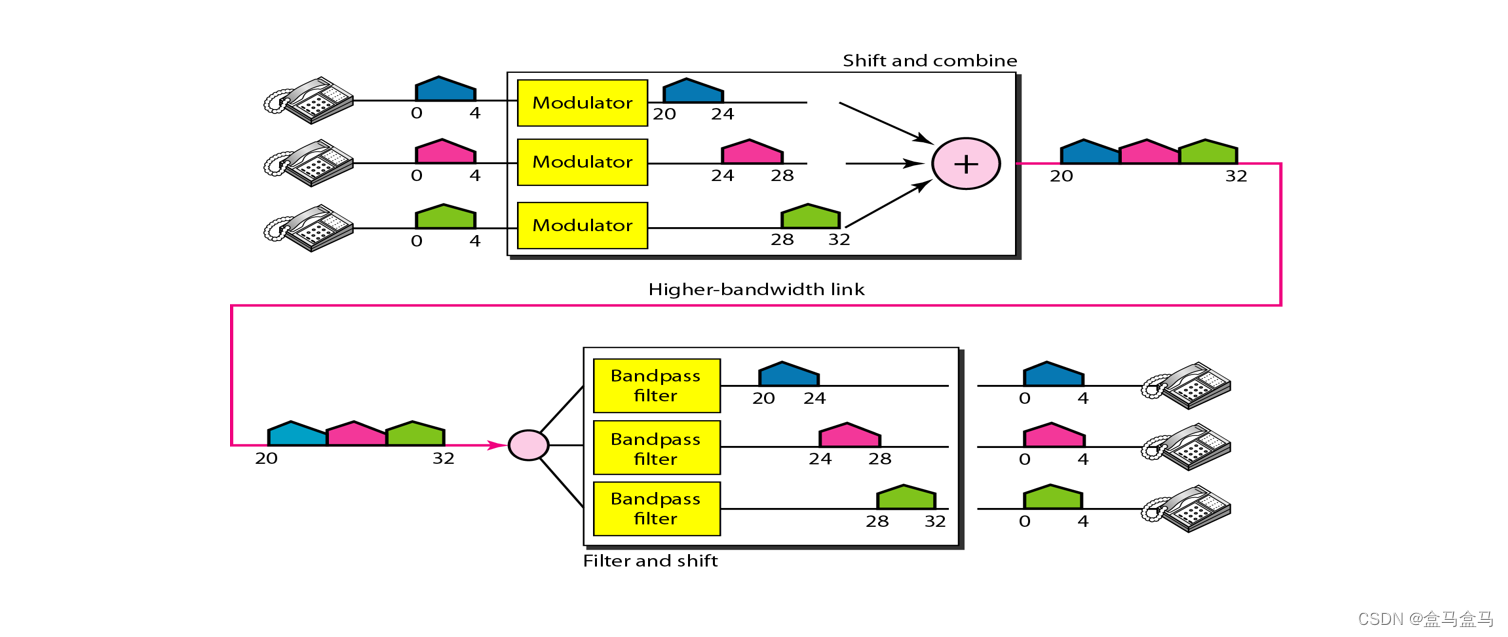
在这里插入图片描述

一开始三个用户都发送了频率范围在0 - 4的信号，经过三个不同的调制器，蓝色信号被调制到了20 - 24，红色信号被调制到了24 - 28，绿色信号被调制到了28 - 32。因为不同信号处于不同频段，将其混合后传输，再经过拆分，又可以拆分出三条数据出来，最后经过解调处理，我们又得到了频率在0 - 4的三条信号。

当然，频分复用也可以叠加：
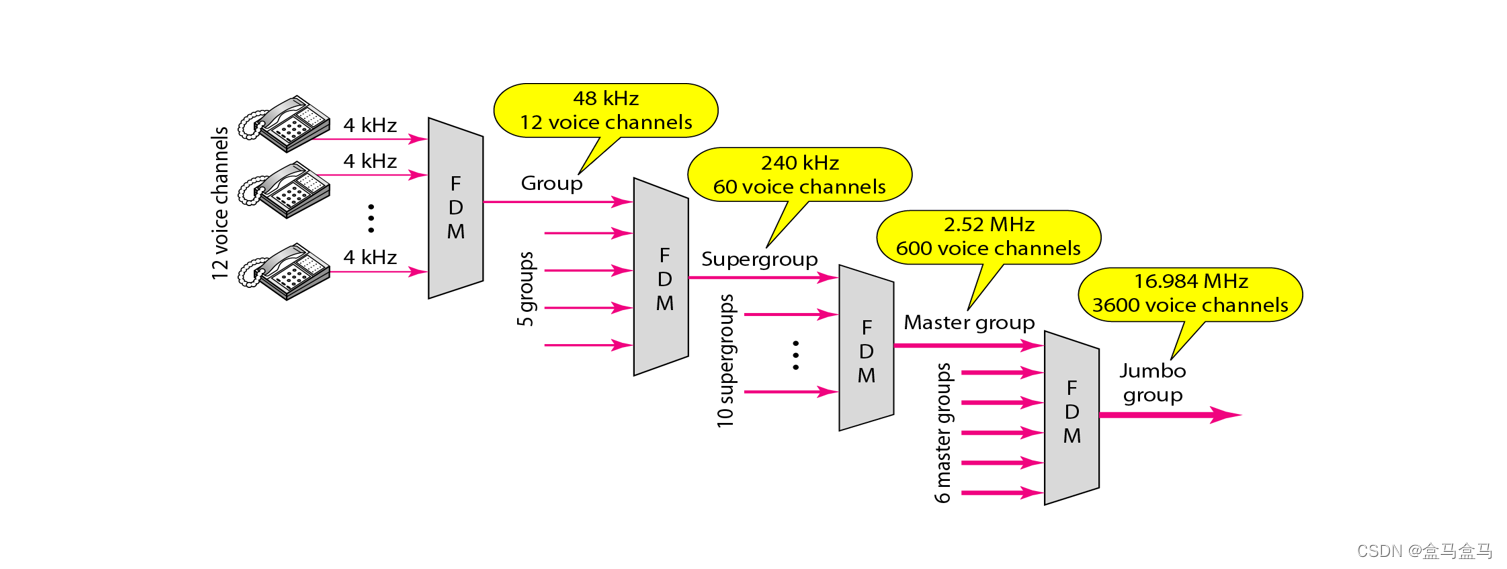
在这里插入图片描述

从左向右，第一次将12条信号进行了调制，第二次把第一次调制出来的混合信号再作为一个信号，拿去进行调制，与其他信号进行频分复用。以此类推，多次叠加下去。

频分复用要求总频率宽度大于各个子信道频率之和，同时为了保证各子信道中所传输的信号互不干扰，应在各子信道之间设立隔离带，这样就保证了各路信号互不干扰。频分复用技术的特点是所有子信道传输的信号以并行的方式工作，每一路信号传输时可不考虑传输时延，因而频分复用技术取得了非常广泛的应用。

时分复用

时分复用就是将提供给整个信道传输信息的时间划分成若干时间片（简称时隙），并将这些时隙分配给每一个信号源使用，每一路信号在自己的时隙内独占信道进行数据传输。时分复用技术的特点是时隙事先规划分配好且固定不变，所以有时也叫同步时分复用。

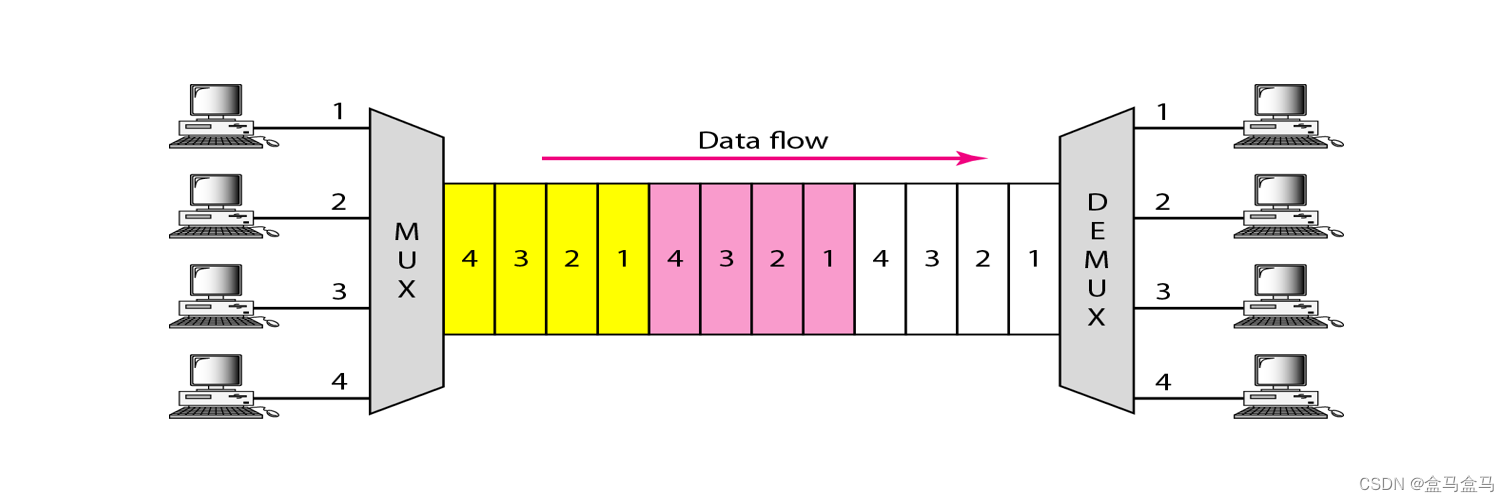
在这里插入图片描述
以上图片就是一个时分复用是示例图，现在我对其进行一个标注：

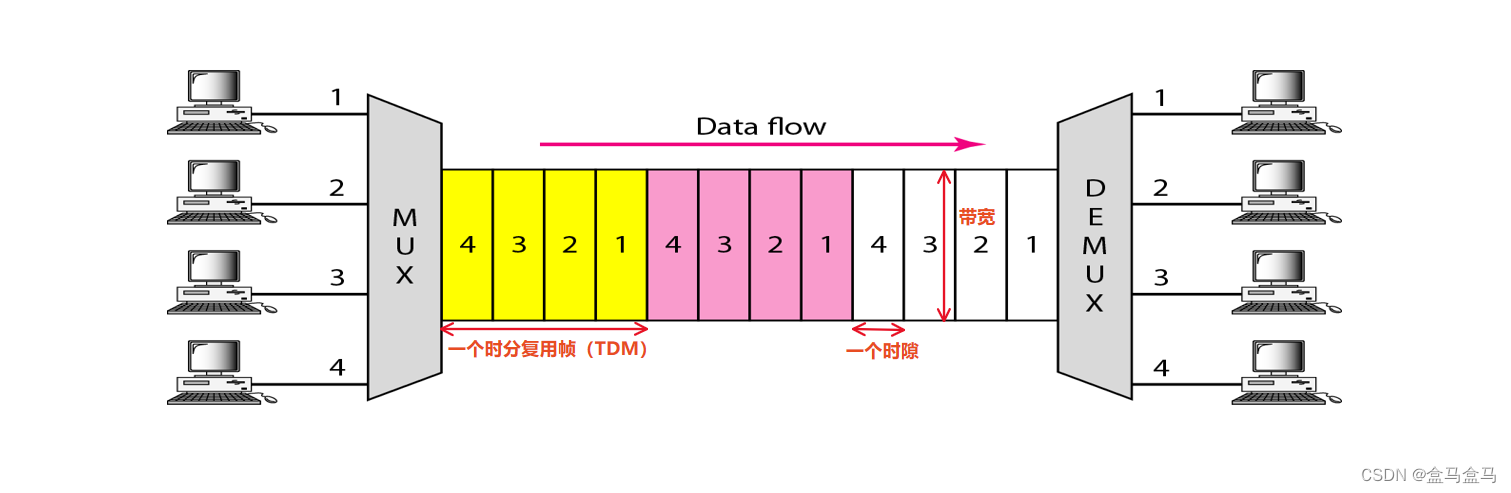
在这里插入图片描述

左侧与右侧的器械：

MUX：信号复用器
DEMUX：信号分用器

我们把一个周期称为一个时分复用帧（TDM帧），在一个周期内部，每个主机发送的信号按照固定的顺序出现，比如这里的顺序就是4 3 2 1，这里的数字代表主机发送的信号。

一个主机发送的信号在一个时分复用帧里面占用的时间叫做一个时隙，通过图片可以看到，在一个时隙内，一个信号占用了整个信道的带宽，也就是独享一个信道。

我们再看到一个量化的例子：
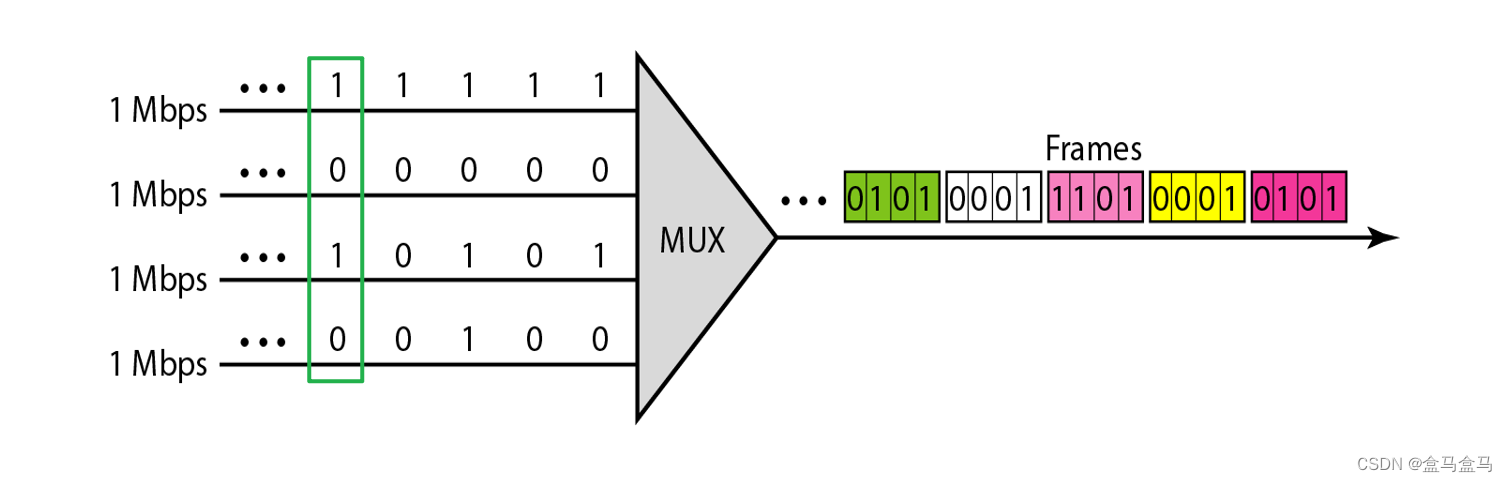
在这里插入图片描述

左侧是四台主机，它们分别发送了一串比特流，经过MUX后，右侧每四个比特组成了一个TDM周期。
左侧的绿色框框部分，就是第一个TDM周期包含的数据，从下往上是0101，因此右侧绿色的第一个TDM周期的数据就是0101。以此类推，后续的0001，1101是如何组成的，也就显而易见了。也就是每台主机提供一个比特位的数据，占用一个时隙，四个时隙构成了一个TDM周期发送出去。这个过程中，四台主机的数据在一个周期中的位置都是固定的。

时分复用的优点是时隙分配固定，便于调节控制，适于数字信息的传输；缺点是当某信号源没有数据传输时，它所对应的信道会出现空闲，而其他繁忙的信道无法占用这个空闲的信道，因此会降低线路的利用率。计算机发送的数据具有突发性，所以经常出现以下情况：

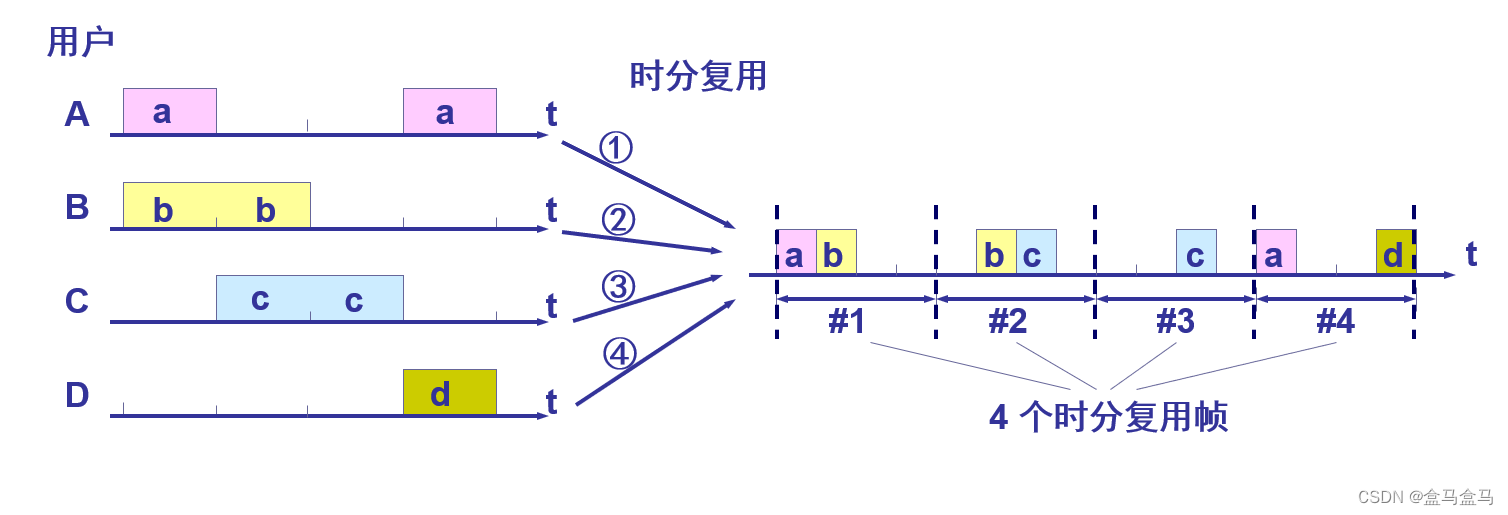
在这里插入图片描述
上图中，由于计算机主机并不会一直持续的发送消息，所以一个TDM周期中，可能只有部分计算机发送了数据，TDM还没有被填满就发送了出去，因此信道利用率比较低。

时分复用技术与频分复用技术一样，有着非常广泛的应用，电话就是其中最经典的例子，此外时分复用技术在广电也同样取得了广泛地应用，如SDH，ATM，IP和HFC网络中CM与CMTS的通信都是利用了时分复用的技术。

统计时分复用

统计时分复用是对时分复用的优化，先前我们的时分复用会出现一个TDM还没有被填满就发送出去，导致信道利用率降低的问题。而统计时分复用优化了这个问题：

在这里插入图片描述
在统计时分复用中，一个周期叫做STDM帧，每次发送数据前，都会等数据把STDM帧填满再发送。但是STDM对数据的顺序不在有要求了。时分复用中，要求每台主机在TDM中占用的时隙位置是固定的。但是统计时分复用只要求填满一个STDM周期，数据的顺序可以是任意的。不过因为缺少了固定的位置来确定目的主机，因此每一个时隙都要额外带上一个目标主机的地址信息。

波分复用

波分复用其实就是光的频分复用。

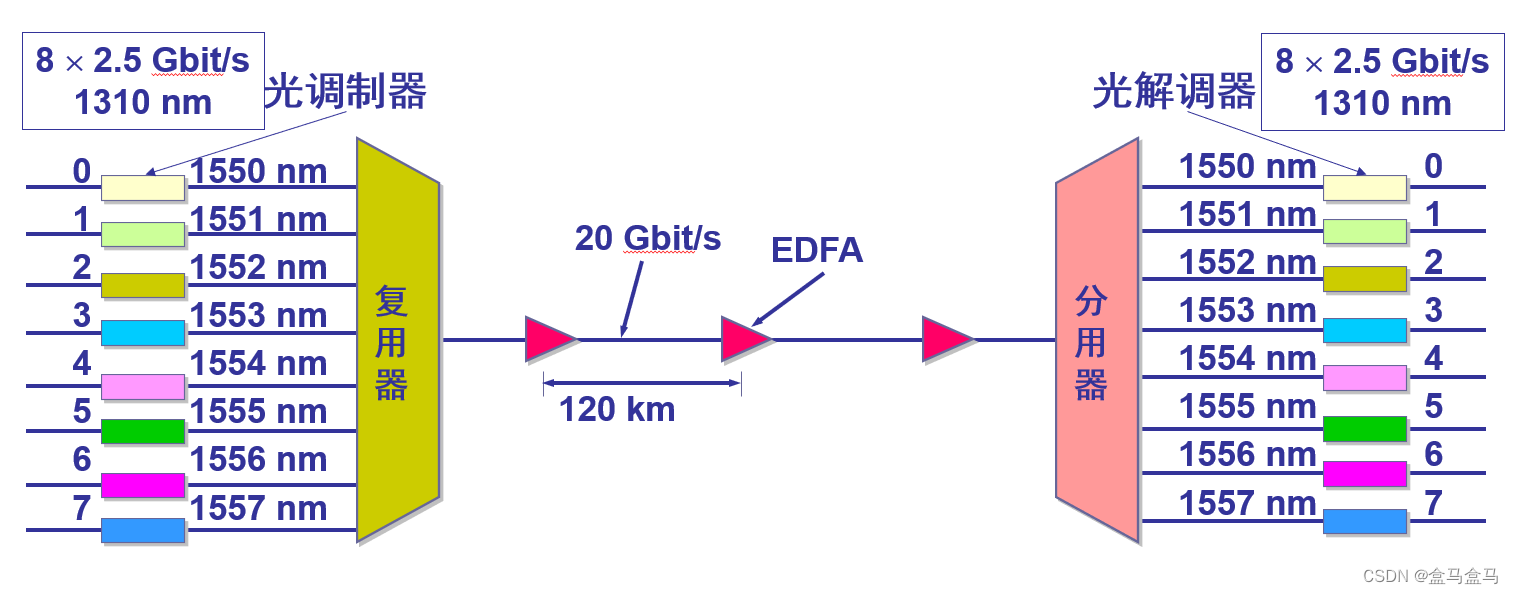
在这里插入图片描述
把光信号调制到不同的频段，然后整合发送出去，接受方再把不同频段的信号拆分出来。

码分复用

码分复用CDM，是靠不同的编码来区分各路原始信号的一种复用方式，通过码分复用共享信道也叫作码分多址CDMA。码分复用是一个比较复杂的复用方式，我们要慢慢讲解。

规则如下：

在码分多址(CDMA)中，比特被重新编码，每一个使用码分多址的站点都拥有一个唯一的码片序列
若发送比特1，则发送自己的码片序列
若发送比特0，则发送该码片序列的二进制反码。

例如，如果S站的8bit码片序列是00011011

如果该站点发送1，那就发送00011011
如果该站点发送0，那就发送11100100

为了方便运算，我们把码片中的0写为-1，1写为+1，因此S站的码片序列为：(-1 -1 -1 +1 +1 -1 +1 +1)。码片序列又叫做码片向量。码片向量有一个非常重要的运算，叫做规格化内积，我们先来了解一下什么叫做规格化内积：

假设我们有一个长度为m的码片向量S，另外一个长度为m的码片向量T，两者规格化内积写作： $\mathrm{S} \bullet \mathrm{T}$
具体运算为：

$\mathrm{S} \bullet \mathrm{T} \equiv \frac{1}{m} \sum_{i=1}^{m} S_{i} T_{i}$

简单来说，就是把两个码片向量的每一位相乘后，求平均值。

假设向量S为(-1 -1 -1 +1 +1 -1 +1 +1)，向量T为(-1 -1 +1 -1 +1 +1 +1 -1)。
两者规格化内积为：
$\mathrm{S} \bullet \mathrm{T} \equiv \frac{{\color{red} (-1) \times (-1)} + {\color{orange} ( -1) \times (-1)} + {\color{gold} (-1) \times 1} + {\color{Green} 1 \times (-1)} + {\color{cyan} 1 \times 1 } + {\color{blue} (-1) \times 1} +{\color{Purple} 1 \times 1} + 1 \times (-1)}{8}$

其中每一种颜色代表一对对应位置的分量，对应位置的分量相乘后求和，最后再除以分量个数8，得到平均值。

CDMA的一个重要特点就是：各个站点的码片向量不仅各不相同，而且两两正交。
所谓码片向量正交，就是两个码片向量规格化内积结果为0。比如刚刚的 $\mathrm{S} \bullet \mathrm{T}$ 就等于0，因此S和T正交。因为每两个站点之间都正交，所以所以站点都满足以下规则：

任何一个码片向量都和其余各站的码片向量规格化内积为0
任何一个码片向量都和其余各站的码片向量的相反向量规格化内积为0
任何一个码片向量和自己规格化内积都是1
任何一个码片向量和自己的相反向量规格化内积都是-1

根据这四条规则，我们的码分复用就可以运作了。我们看到一个示例：
共有四个站进行 CDMA 通信，四个站的码片序列为:

A：(-1 -1 -1 +1 +1 -1 +1 +1)
B：(-1 -1 +1 -1 +1 +1 +1 -1)
C：(1 +1 -1 +1 +1 +1 -1 -1)
D：(-1 +1 -1 -1 -1 -1 +1 -1)

现在收到一个码片序列为：R：(-1 +1 -3 +1 -1 -3 +1 +1)
那么每个站发送的信号是什么？

对于这个问题，我要先说明，如果ABCD同时发送消息，此时会把ABCD的码片向量全部进行规格化内积，也就是 $\mathrm{A} \bullet \mathrm{B} \bullet \mathrm{C} \bullet \mathrm{D}$ ，就得到了一个混合码片向量R。

根据规则1和规则2：一个站点的码片向量和其它站点规格化内积一定是0，因此如果和这个混合向量R规格化内积，结果为0，说明这个混合向量中没有该站点发送的信息。
根据规则3：如果某个站点和这个混合向量R规格化内积结果为1，说明该站点发送了自己的码片向量，也就是发送了bit1。
根据规则4：如果某个站点和这个混合向量R规格化内积结果为-1，说明该站点发送了和自己相反的码片向量，也就是发送了bit0。

经过计算，得到：

$\mathrm{A} \bullet \mathrm{R} \equiv 1$ ：说明混合向量R中存在A自己的码片向量，A站点发送了1
$\mathrm{B} \bullet \mathrm{R} \equiv -1$ ：说明混合向量R中存在B自己的码片向量相反向量，B站点发送了0
$\mathrm{C} \bullet \mathrm{R} \equiv 0$ ：说明混合向量R中不存在C发送的向量，因此C站点没有发送信号
$\mathrm{D} \bullet \mathrm{R} \equiv 1$ ：说明混合向量R中存在D自己的码片向量，D站点发送了1