根据前中序遍历顺序构建一个二叉树

力扣练习链接

过程

总体框架

• 设preorder的左边界为pleft,右边界为pright[注意这里是闭区间能取到]
• 同时设inorder的左边界为ileft,有边界为iright[同样也是可以取到的索引区间]
• 我们生成每一个区间的树的头结点,然后向上返回,对于他的父亲结点,利用子树的返回值作为左右子节点

递归结构的设计

当区间内只有一个结点，继续遍历，直到区间取到空的树判断是否结束

• 如果遍历到的右子树是空的,那么下一次会出现这种情况:ileft>iright

• 同样的,如果左子树是空的,那么下一次会出现:iright<ileft
  所以结束条件这样去设计：

  if (ileft>iright||iright<ileft) return nullptr;

  去返回一个空的指针

寻找左右子树

1. 对于以前序和中序遍历的树,他的结构如下:
   

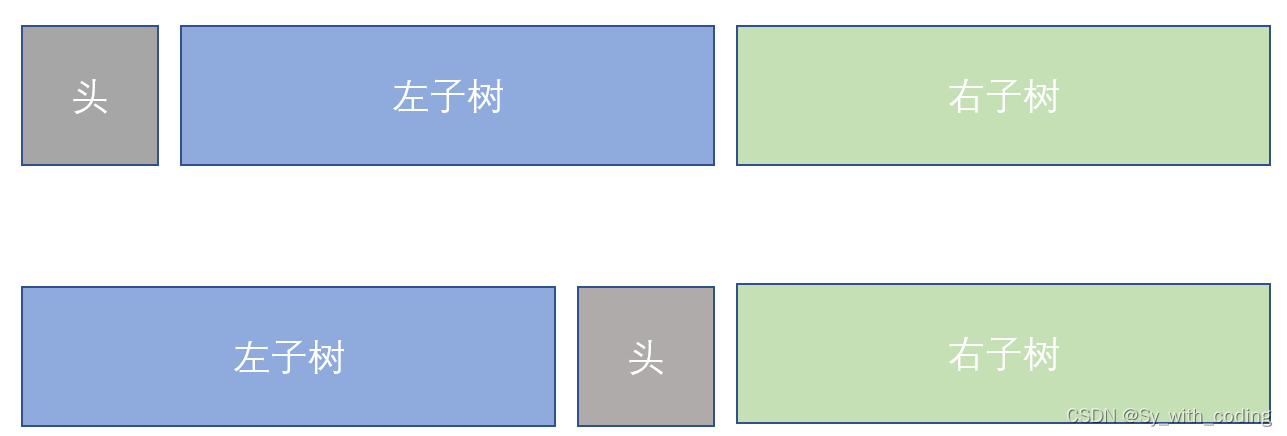
   遍历一遍 inorder 数组, 将所有的元素的以<元素值, 索引值>的结构存入哈希表中
   根结点的值就是inorder数组中的首元素
   但是我们需要在preorder中去找到根节点的索引位置
   通过之前构建哈希表,我们可以直接用头结点的值来得到它在inorder数组中的索引下标
   以左子树的区间为例, 在inorder和preorder区间中的长度相等,所以可以得到这样的等式:
   

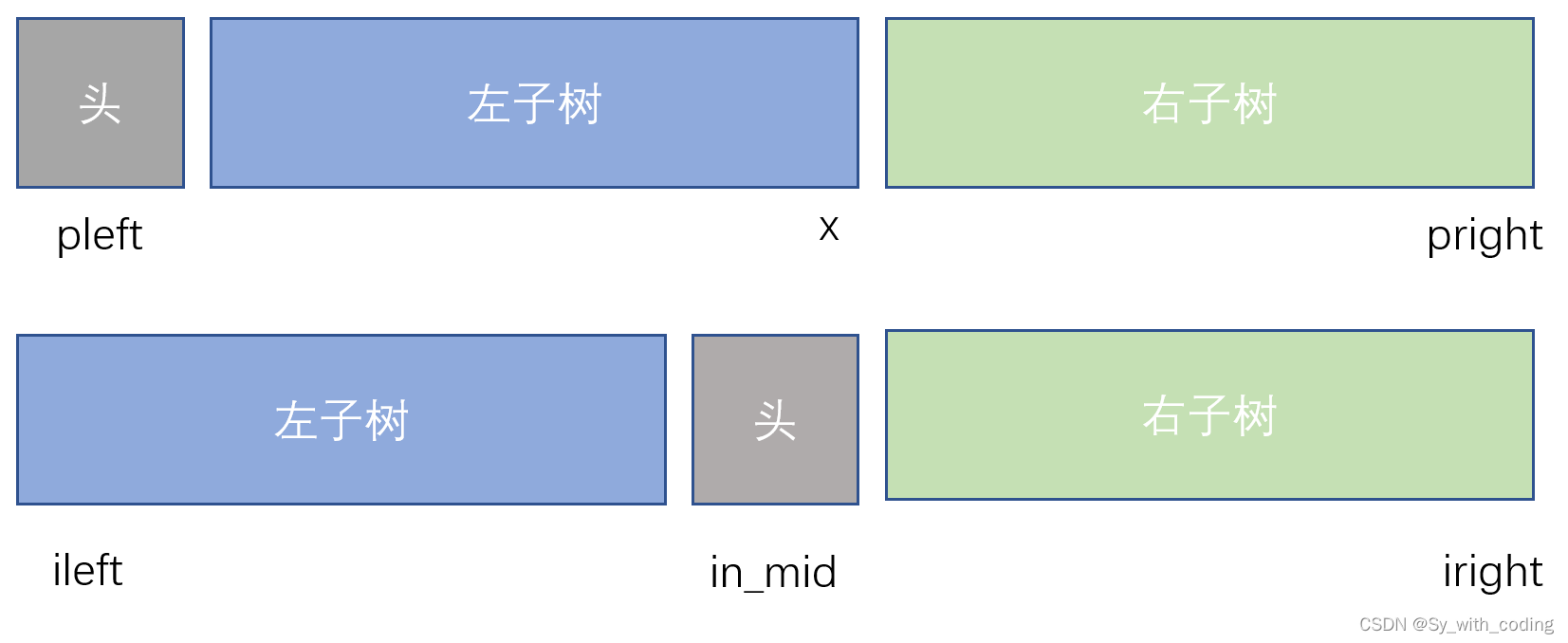
   in_mid-ileft = x - pleft

2. 这样我们就得到了左子树的区间,preorder:[pleft+1, x]
   ineorder:[ileft, in_mid-1]

3. 同样的,对于右子树的区间,preorder:[x+1, pright]
   ineorder:[in_mid+1, iright]

Coding

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:unordered_map<int, int> hash;TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int size = preorder.size();for (int i = 0; i < size; i++) {hash[inorder[i]] = i;}return f(preorder, inorder, 0, size-1, 0, size-1);}TreeNode* f(vector<int>& preorder, vector<int>& inorder, int pleft, int pright, int ileft, int iright) {if (ileft>iright || iright<ileft) {return nullptr;}int pleftValue = preorder[pleft];TreeNode* root = new TreeNode(pleftValue);int in_mid = hash[pleftValue];int x = pleft + in_mid - ileft;root->left = f(preorder, inorder, pleft+1, x, ileft, in_mid-1);root->right = f(preorder, inorder, x+1, pright, in_mid+1, iright);return root;}
};