题目链接:
蓝桥杯2023年第十四届省赛真题-异或和之和 - C语言网 (dotcpp.com)
1.异或和之和 - 蓝桥云课 (lanqiao.cn)
参考题解:
蓝桥杯真题讲解:异或和之和 (拆位、贡献法)-CSDN博客
洛谷P9236 [蓝桥杯 2023 省 A] 异或和之和 题解_c加加区间异或问题洛谷ir-CSDN博客
说明:
1.需要知道一个重要的结论(图片来自参考题解):
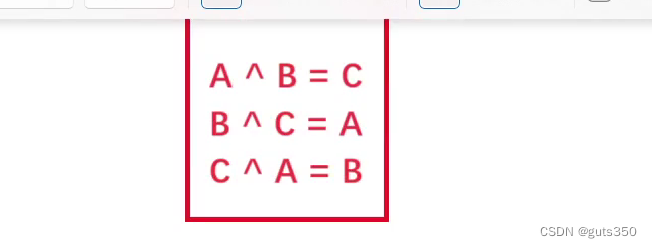
注:为什么A^B=C可以得到B^C=A ?在原式上两边同时异或上一个B,根据异或的性质,B^B=0,与0异或等于本身。
2.那么由前缀和可以得出
(sum(j,i)为i和j这个区间上面的异或和,右下角第二排的式子等号两边同时异或上一个s[j-1]得到第一排的式子):
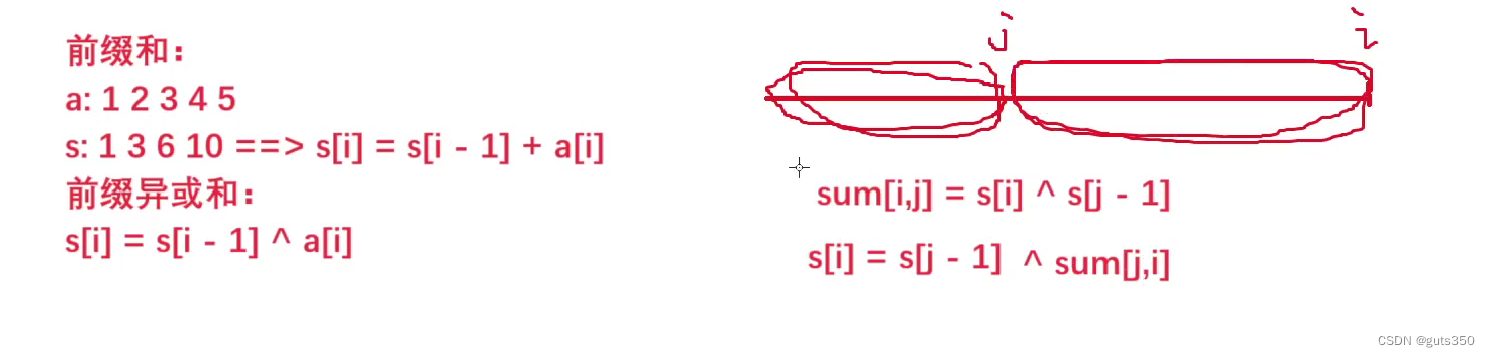
3.从推出的这个式子来看,sum[i,j]=s[i]^s[j-1],(i右端点,j左端点)
说明任意一个区间上面的异或和都可以转化成两个异或前缀和的异或和。再考虑到,对于一个二进制位来说,异或和结果为1的时候才会对结果有影响(贡献),而奇数个1异或为1,偶数个为0,对应到这里的两个数(前缀和)异或,那么就是一个前缀和为0,一个为1,那么把n个数都进行拆位,就可以 对每一个二进制位 做操作数是0或1(只有拆成二进制的0和1才能直接用前面的结论)的异或位运算。
于是统计,在第k位(从0开始数)上,n个数中对应前缀和为0、1的数量,记为n0,n1,那么最后在这一位上的对结果的贡献就是n0*n1* 。
这里注意:需要把S[0]考虑进来,左端点位置为1的时候计算区间需要s[0] ,而S[0]为0 ,所以0的初始数量为1
为什么会是n0 * n1 * ?因为n0是前缀和为0的数量,n1是前缀和为1的数量,我们在n0个位置里面选一个,再在n1个位置里选一个,他们计算出来的区间异或和sum(i,j)是为1的,且这个sum(i,j)不重复,因为你计数的0和1的位置是不重复的,那么计算出来的sum(i,j)的至少由一个端点跟别的sum不一样,那么n0*n1是sum(i,j)为1的个数,乘上这一位上的基数即可。
4.另一种思路:
在参考题解第二个文章里,提出了另一种思路,既然
对于一个二进制位来说,异或和结果为1的时候才会对结果有影响(贡献),而奇数个1异或为1,偶数个为0
那么我统计我当前位置是出现1的奇数次还是偶数次,根据
sum[i,j]=s[i]^s[j-1]
为奇数次,s[i]为1,要求s[j-1]为偶数次;
为偶数次,s[i]为0,要求s[j-1]为奇数次(即要求总的次数为奇数)。
于是很容易去找(记前面为偶数次的 位置数 为 even,奇数次为odd):
s[i]为奇数次,是不是就有 even+1个 为奇数次1 的区间?(因为这even个偶数次的 位置都可以作为s[j-1]的这个j-1位置,还有s[0]=0,0也是偶数次,这个没被计数到,(1,i)也是一个奇数个的区间,所以还要加1)
s[i]为偶数次,是不是就有 odd个 为奇数次1 的区间,因为是要求s[j-1]为奇数次,所以不加1.
或者可以这样考虑:
s[i]为奇数次,even个前面为偶数次的 位置,这些位置第一次出现对应的数肯定是1,且这个1只出现一次(对应这个偶数),否则1的数量就变了,0可以出现无数次,那么就是对应一个偶数o,他出现的第一个位置m,a[m](假设a为第k位上,这n个数的01序列的数组名)为1,s[m-1]肯定只出现了o-1次,这个位置不能组成合法区间,去掉。
而对于一个奇数p,第一次出现的位置r,a[r]为1,s[r-1]为偶数次p-1,需要加上这个位置。
于是合法的区间=even-出现的偶数的数量(若出现2,4,则数量为2)+出现的奇数的数量
当s[i]为奇数次,奇数的数量比偶数数量多1,推出上面同样的式子。
s[i]为偶数次,二者相等,推出上面同样的式子。
5.注意:
数据范围,数组每个数小于等于2的20次方,那么要考虑的二进制位数就是21位,不是20位!!
代码:
仅异或前缀和
要枚举左右端点,时间复杂度 ,会超时。60%数据。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int ans=0;
int a[N];
int s[N];//异或前缀和 //vector<int> num[N];
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];//ans+=a[i];s[i]=s[i-1]^a[i];}for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){int sum=s[j]^s[i-1];// sum(i,j)^s[i-1]=s[j]两百年同时异或s[i-1]消掉左边的 s[i-1]ans+=sum;}}cout<<ans;return 0;
}说明3对应代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int ans=0;
int a[N];
int s[N];
//异或前缀和
int odd,even,cnt=0,radix=1;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i]; }radix=1;for(int i=0;i<=20;i++){//这里同样注意:需要把S[0]考虑进来,左端点位置为1的时候计算区间需要s[0] ,而S[0]为0 //所以0的初始数量为1 int n0=1,n1=0;for(int j=1;j<=n;j++){//求第i位上的二进制前缀和 s[j]=s[j-1]^(a[j]&1);if(s[j]==1){n1++;} else{n0++;}a[j]=a[j]>>1;}ans+=n0*n1*radix;radix=radix<<1;}cout<<ans;return 0;
}
说明4对应代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int ans=0;
int a[N];
int s[N];
//异或前缀和
int odd,even,cnt=0,radix=1;
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}// 对二进制的21个位置中的第j个位置算n个数的贡献 //注意:是 0-20位!!!有21个位置 for(int j=0;j<=20;j++){cnt=0;odd=0,even=0;//对第i个数而言,它的二进制形式的第j位(从0开始数),能找到的能贡献1的区间数,//这个区间是i和前i个数组成的。有多少个能贡献1的区间在第i位上结果就加上多少个1 (最后结果要乘上第j位对应的基数:2的j次方) for(int i=1;i<=n;i++){//对n个数计算第j位上的异或和之和 //注意:取出最后一位的方法 int tt=a[i]&1;//取出二进制位 if(tt==1){//计算二进制第j位上,到第i个数是出现了几个1,用前缀和累加可以在O(1)复杂度计算出 s[i]=s[i-1]+1;}else{s[i]=s[i-1];}if(s[i]%2==0){//到第i数出现了偶数个1,那么他能找到 前i项中为奇数次的数量 个贡献1的区间 even++;ans+=(odd)*radix;//注意乘上第j位对应的基数 }else{//到第i数出现了奇数个1,那么他能找到 前i项中为偶数次的数量+1 个贡献1的区间 odd++;ans+=(even+1)*radix;}a[i]=a[i]>>1;//第i个数左移一位,方便下一次取j+1位 }radix=radix<<1;//j+1位,基数变成原来的2倍 }// for(int i=1;i<=n;i++){
// for(int j=i;j<=n;j++){
// int sum=s[j]^s[i-1];// sum(i,j)^s[i-1]=s[j]两百年同时异或s[i-1]消掉左边的 s[i-1]
// ans+=sum;
// }
// }cout<<ans;return 0;
}