目录
- 引入
- 什么是动态规划?
- 动态规划的特点
- 解题办法
- 解题套路框架
- 举例说明
- 斐波那契数列
- 题目描述
- 解题思路
- 方式一:暴力求解
- 思考
- 方式二:带备忘录的递归解法
- 方式三:动态规划
- 推荐练手题目
引入
动态规划问题(Dynamic Programming)应该是很多人头疼的一类问题,
本文尝试探索一种套路帮助解决此类问题
什么是动态规划?
动态规划的核心思想是将问题分解为一系列子问题,并通过记忆化或递推的方式求解子问题,从而得到原始问题的解。
动态规划的特点
其主要特点包括:
- 重叠子问题:问题的解能够通过多次重复计算相同的子问题得到。
- 最优子结构:问题的最优解能够由子问题的最优解推导得出。
解题办法
动态规划通常分为自顶向下的记忆化搜索和自底向上的递推两种方法。
解题套路框架
解决动态规划问题通常遵循以下套路框架:
递归的暴力解法 -> 带备忘录的递归解法 -> 非递归的动态规划解法。这个过程是层层递进的解决问题的过程,
具体的过程
-
确定状态
需要明确问题的状态是什么,以及在状态转移过程中如何更新状态。 -
定义状态转移方程
状态转移方程描述了状态之间的转移关系。它明确了如何从已知的状态计算出未知状态的值。 -
处理边界条件
边界条件是指状态转移的起点或终点,通常需要单独考虑和处理。 -
计算动态规划数组
使用循环遍历计算动态规划数组中的每个元素,根据状态转移方程填充数组。 -
返回结果
根据问题的具体要求,从动态规划数组中选取相应的值作为最终的结果。
举例说明
以下是一个使用动态规划解决斐波那契数列问题的示例:
斐波那契数列
题目描述
斐波那契数列是一个非常经典的数列,它的第一个和第二个数分别为 0 和 1,从第三个数开始,每个数都是前两个数之和。即斐波那契数列的定义如下:F(0) = 0,
F(1) = 1,
F(n) = F(n-1) + F(n-2) (n >= 2)给定一个整数 n,编写一个函数来计算斐波那契数列中第 n 个数的值。例如:输入:n = 0,输出:0
输入:n = 1,输出:1
输入:n = 5,输出:5
输入:n = 10,输出:55
解题思路
方式一:暴力求解
以java为例
public class Fibonacci {// 暴力递归求解斐波那契数列public static long fibonacci(int n) {// base caseif (n == 0) {return 0;} else if (n == 1) {return 1;} else {// 递归计算前两个数的和return fibonacci(n - 1) + fibonacci(n - 2);}}public static void main(String[] args) {int n = 10;long result = fibonacci(n);System.out.println("The Fibonacci number at position " + n + " is: " + result);}
}说明:
fibonacci方法用于求解第n个斐波那契数,采用递归的方式。
在方法中,首先判断n的值是否为0或1(即基本情况),如果是则返回对应的斐波那契数值。
如果n值大于1,则通过递归计算前两个数的和,即fibonacci(n-1) + fibonacci(n-2)。
在main方法中,我们定义一个整型变量n表示所求的斐波那契数的位置,然后调用fibonacci方法计算结果。
最后,打印出所求位置上的斐波那契数。
思考
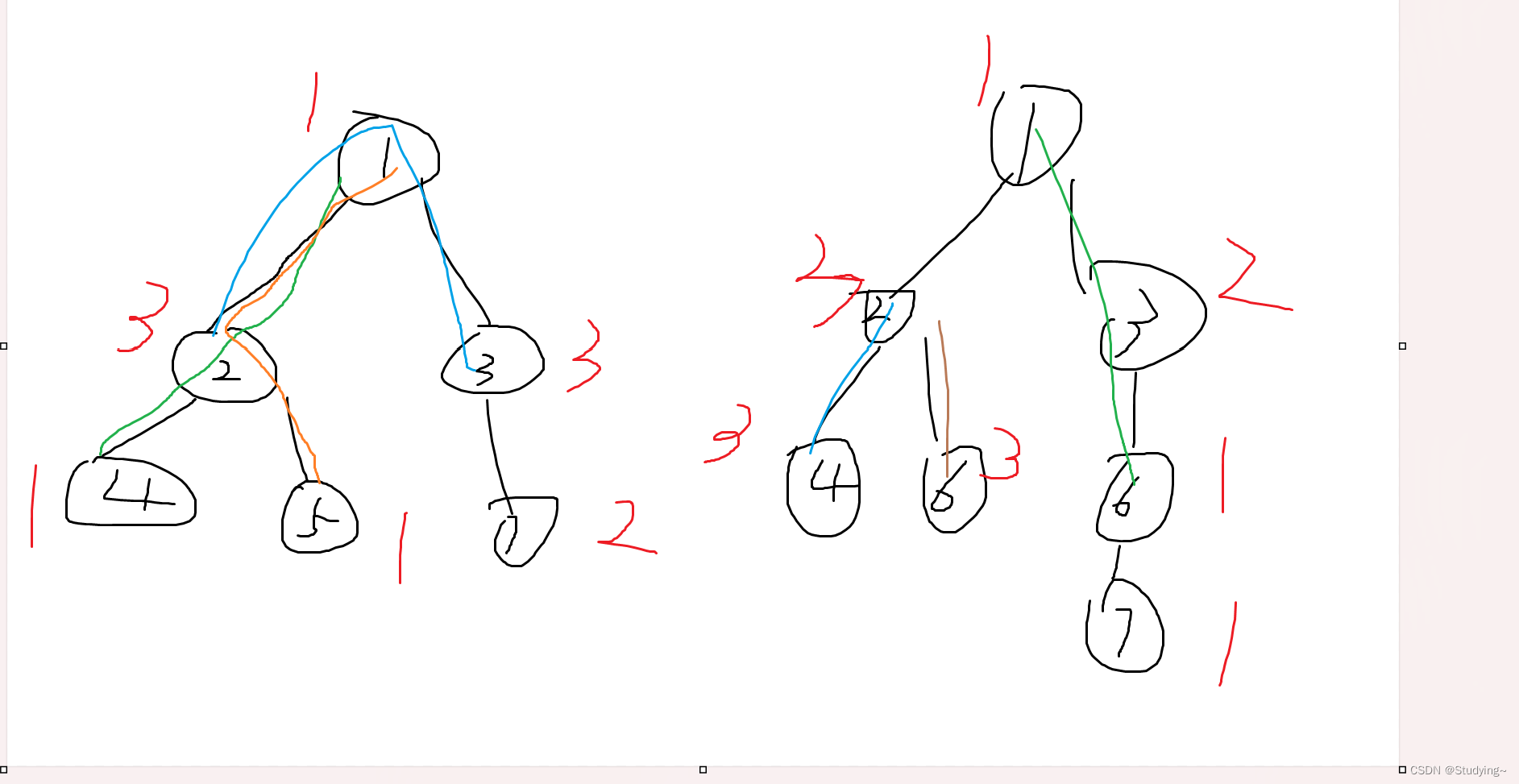
学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树。
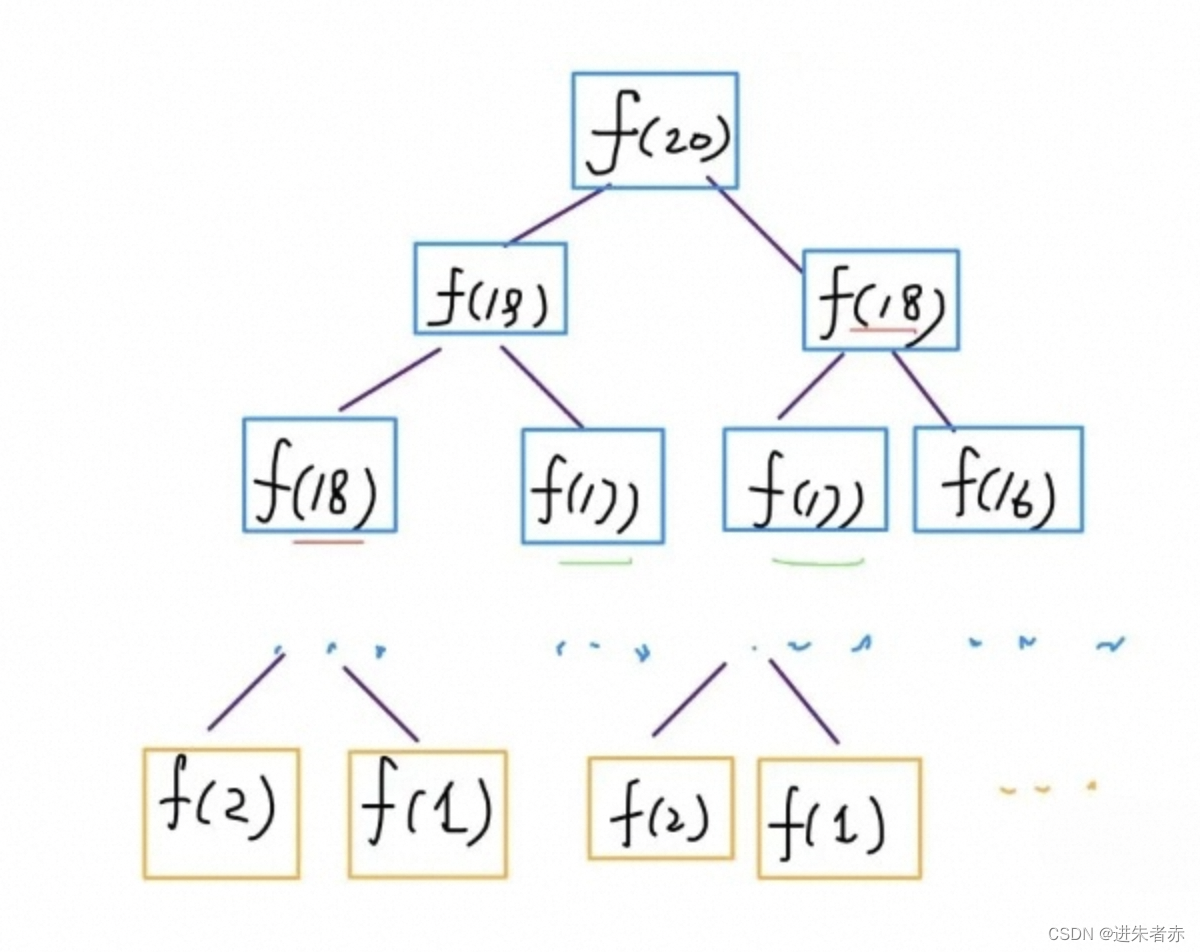
递归树是一种用于理解递归算法执行过程的图形表示方法。对于斐波那契数列问题,在递归过程中,我们可以将其表示为一棵递归树。递归树的每个节点表示一个子问题,根节点表示原问题。以计算 f(20) 为例,我们需要先计算子问题 f(19) 和 f(18),然后计算 f(19) 时又需要先计算子问题 f(18) 和 f(17),依此类推。当到达 f(1) 或 f(2) 时,可以直接返回已知的结果,递归树不再向下生长。
递归算法的时间复杂度可以通过计算子问题个数乘以解决一个子问题所需时间来得到。子问题个数指的是递归树中节点的总数。显然,在斐波那契数列的递归树中,节点总数为指数级别,即 O(2^n)。而解决一个子问题的时间,在这个算法中是常数级别的(O(1)),因为只有一个加法操作。
因此,该算法的时间复杂度为 O(2^n),是指数级别的,效率低下。
观察递归树可以明显看出算法低效的原因:存在大量的重复计算。例如,节点 f(18) 被计算了两次。而且不仅仅是节点 f(18),还有其他节点也被重复计算。因此,这个算法非常低效。
动态规划问题具备的第一个性质就是重叠子问题。接下来,我们将想办法解决这个问题。
方式二:带备忘录的递归解法
明确了重复计算是导致算法低效的主要原因后,我们可以采取一种优化策略,即使用一个「备忘录」来避免重复计算。每次计算完一个子问题的答案后,不急于返回,而是将答案存储在「备忘录」中。下次遇到同样的子问题时,先查找「备忘录」,如果已经计算过了,直接取出答案使用,避免重复计算。
通常情况下,我们可以使用数组来充当「备忘录」,但也可以使用哈希表(字典)等其他数据结构,核心思想是一样的。
java实现:
import java.util.HashMap;
import java.util.Map;public class Fibonacci {// 使用备忘录来避免重复计算private static Map<Integer, Long> memo = new HashMap<>();public static long fibonacci(int n) {// 查找备忘录,如果已经计算过,直接返回答案if (memo.containsKey(n)) {return memo.get(n);}// Base caseif (n == 0) {return 0;} else if (n == 1) {return 1;}// 计算并记录答案到备忘录中long ans = fibonacci(n - 1) + fibonacci(n - 2);memo.put(n, ans);return ans;}public static void main(String[] args) {int n = 20;long result = fibonacci(n);System.out.println("The Fibonacci number at position " + n + " is: " + result);}
}说明:
我们使用一个哈希表(字典)memo作为「备忘录」,用于存储子问题的答案。在fibonacci方法中,首先查找「备忘录」,如果已经计算过子问题n的答案,则直接返回答案。这样就避免了重复计算。
接下来,处理基本情况,即斐波那契数列的前两个数。
然后,通过递归计算并记录答案到「备忘录」中,即计算fibonacci(n-1) + fibonacci(n-2)并将结果存入memo。 最后,返回计算结果。
现在,画出递归树,你就知道「备忘录」到底做了什么。
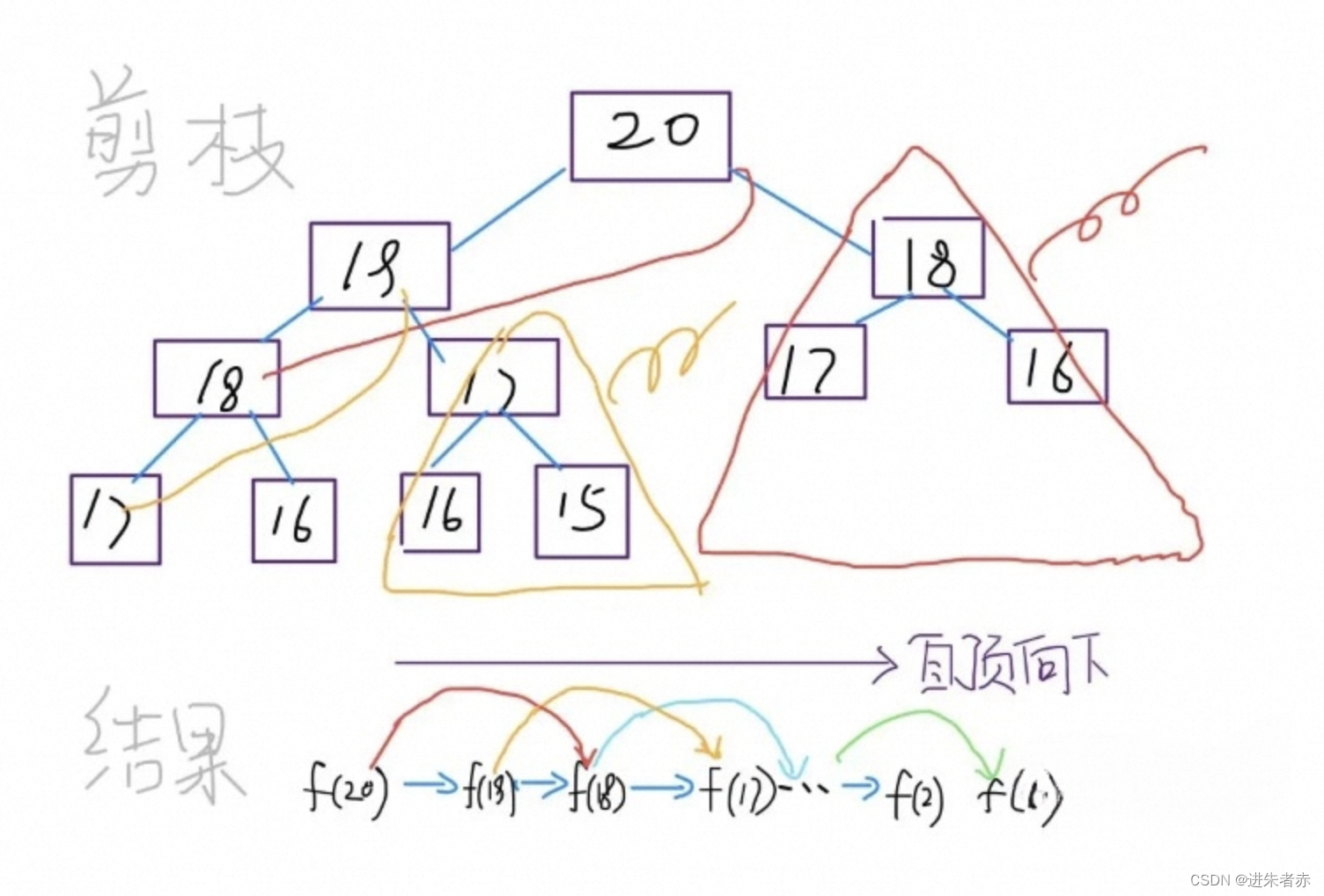
使用带有备忘录的递归算法时,我们可以将其思路分为以下几个层次进行说明:
-
第一层次:理解问题存在重复计算导致低效
我们首先明确问题的低效之处在于重复计算。观察递归树,我们发现存在大量的重复计算,例如节点 f(18) 被计算了两次,这样会浪费大量的时间。 -
第二层次:引入「备忘录」概念
为了避免重复计算,我们引入了「备忘录」的概念。在计算完一个子问题的答案后,我们将其结果存储在「备忘录」中。下次遇到相同的子问题时,先查找「备忘录」,如果已经计算过,直接返回结果,从而避免重复计算。 -
第三层次:优化时间复杂度
递归算法的时间复杂度可以通过计算子问题个数乘以解决一个子问题所需的时间来得到。对于带有备忘录的递归算法,子问题个数是与输入规模成正比的,因为我们使用备忘录避免了重复计算。解决一个子问题的时间仍然是常数级别。因此,该算法的时间复杂度为 O(n),相比于暴力算法有了显著的降低。 -
第四层次:对比「自顶向下」和「自底向上」
我们进一步将带有备忘录的递归解法与动态规划进行对比。带有备忘录的递归解法采用了「自顶向下」的思路,通过递归树从顶部向下延伸,逐步分解规模,直到达到基础情况并逐层返回答案。而动态规划采用了「自底向上」的思路,从最底部、最简单、规模最小的问题开始向上推导,直到得到所需的答案。动态规划通常通过迭代循环实现计算,不使用递归。
通过以上层次的分析进一步理解带有备忘录的递归算法的优势,并将其与动态规划进行对比,有助于深入理解动态规划思想的应用。
方式三:动态规划
java实现
public class Fibonacci {public static long fibonacci(int n) {// 创建一个数组来存储子问题的解,初始值为0long[] dp = new long[n + 1];// 初始化前两个数的值dp[0] = 0;dp[1] = 1;// 从第三个数开始迭代计算for (int i = 2; i <= n; i++) {// 通过状态转移方程计算当前数的值dp[i] = dp[i - 1] + dp[i - 2];}// 返回第n个数的值return dp[n];}public static void main(String[] args) {int n = 20;long result = fibonacci(n);System.out.println("The Fibonacci number at position " + n + " is: " + result);}
}说明:
创建一个数组dp来保存子问题的解,数组的长度为n + 1,初始值都为0。 初始化数组中的前两个数,即dp[0] = 0和dp[1]= 1,这是斐波那契数列的基础情况。 从第三个数开始,使用循环迭代计算每个数的值。通过状态转移方程dp[i] = dp[i - 1] + dp[i - 2],计算当前数的值,即前两个数之和。 最后,返回第n个数的值,即为斐波那契数列中第n个数的结果。```
通过绘制 DP Table,可以更好地理解动态规划解法。而且你会发现,DP Table 实际上与带有备忘录的递归解法中的「备忘录」非常相似,只是顺序相反而已。事实上,当备忘录完成填充后,就形成了这个 DP Table。因此,这两种解法在很大程度上是相似的,而且在大多数情况下,它们的效率也基本相同。
在这里,我们引入了「状态转移方程」这个名词,实际上它描述的是问题结构的数学形式:
F(n) = F(n-1) + F(n-2)
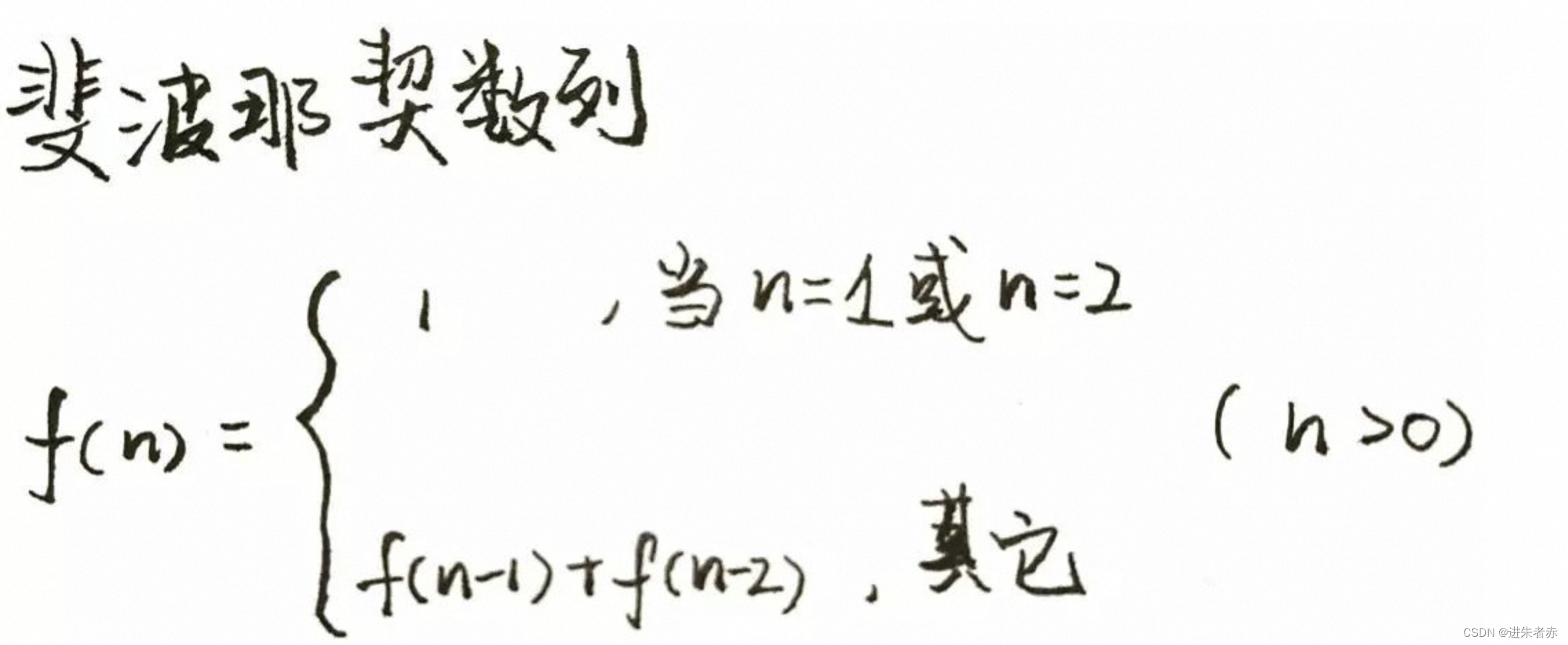
这个方程告诉我们,要计算第 n 个斐波那契数,我们只需要知道前两个数的值即可。通过这个方程式,我们可以将问题的求解转化为子问题的求解。
「状态转移方程」这个术语可能听起来有些高级,其实它的含义很简单。在斐波那契数列问题中,我们将 f(n) 看作是一个状态 n,而这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来。所以,「状态转移方程」就是描述问题中不同状态之间的变化关系而已。它帮助我们理解问题的结构并找到解决方法。
动态规划的精髓就是找到合适的状态转移方程,它能够将大问题拆分成小问题,并且小问题的结果可以用于求解大问题。在斐波那契数列问题中,状态转移方程适用于计算任意位置的斐波那契数。
因此,通过定义好状态转移方程并利用它,我们可以构建出 DP Table 或使用递归加备忘录的方式来高效地求解斐波那契数列问题。
这只是一个简单的示例,实际的动态规划问题可能会更复杂。但遵循这个解题套路框架,通过确定状态、定义状态转移方程、处理边界条件、计算动态规划数组和返回结果,可以更好地解决各种不同类型的动态规划问题
推荐练手题目
| 序号 | 题目名称 | 题目描述 | 难度 | 题目链接 |
|---|---|---|---|---|
| 1 | 爬楼梯(Climbing Stairs) | 有n个台阶,每次可以爬1个或2个台阶,求爬到第n个台阶的所有可能的方法数。 | 简单 | LeetCode 70 |
| 2 | 最长递增子序列(Longest Increasing Subsequence) | 给定一个整数数组,找到其中最长的递增子序列的长度。 | 中等 | LeetCode 300 |
| 3 | 背包问题(Knapsack Problem) | 有一个背包可以容纳一定重量的物品,给定一组物品的重量和价值,选择一部分物品放入背包,使得选中的物品总重量不超过背包容量,同时总价值最大。 | 中等 | LeetCode 322 |
| 4 | 打家劫舍(House Robber) | 给定一列房屋,每个房屋中都有一定数量的金额,相邻的房屋不能同时被盗窃。求能够盗窃的最大金额。 | 简单 | LeetCode 198 |
| 5 | 解码方法(Decode Ways) | 给定一个只包含数字的非空字符串,判断是否有可能解码成字母组合。每个数字转换为对应的字母(A - 1,B - 2,…,Z - 26)。 | 中等 | LeetCode 91 |





![[Semi-笔记]Switching Temporary Teachers for Semi-Supervised Semantic Segmentation](https://img-blog.csdnimg.cn/direct/2499c7feca1b4841aaf9e8b28e412fd6.png)