DFS：深搜+回溯+剪枝解决矩阵搜索问题

创作不易，感谢三连！！

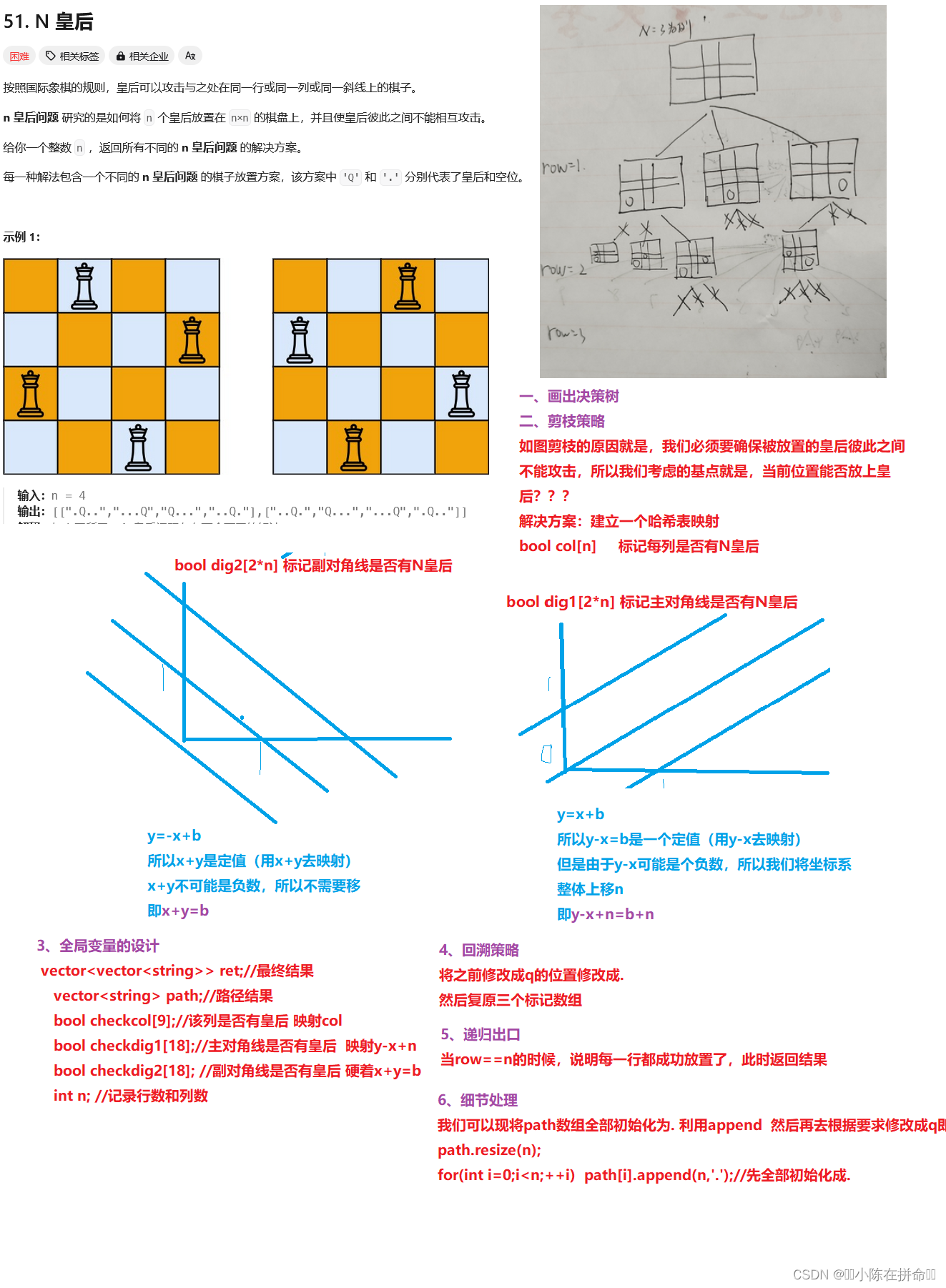
一、N皇后

. - 力扣（LeetCode）

class Solution {
public:vector<vector<string>> ret;vector<string> path;bool checkcol[9];bool checkdig1[18];bool checkdig2[18];int n;vector<vector<string>> solveNQueens(int _n) {n=_n;path.resize(n);for(int i=0;i<n;++i)  path[i].append(n,'.');//先全部初始化成.dfs(0);return ret;}void dfs(int row){if(row==n) {ret.push_back(path);return;}for(int col=0;col<n;++col)//枚举每一行的每个元素{if(checkcol[col]==false&&checkdig1[n+row-col]==false&&checkdig2[row+col]==false)//n+row-col防止越界{path[row][col]='Q';checkcol[col]=checkdig1[n+row-col]=checkdig2[row+col]=true;dfs(row+1);//恢复现场path[row][col]='.';checkcol[col]=checkdig1[n+row-col]=checkdig2[row+col]=false;}}}
};

二、有效的数独

. - 力扣（LeetCode）

class Solution {
public:bool checkrow[9][10];bool checkcol[9][10];bool checkgrid[3][3][10];bool isValidSudoku(vector<vector<char>>& board) {for(int row=0;row<9;++row){for(int col=0;col<9;++col){if(board[row][col]!='.'){int num=board[row][col]-'0';if(checkrow[row][num]||checkcol[col][num]||checkgrid[row/3][col/3][num]) return false;checkrow[row][num]=checkcol[col][num]=checkgrid[row/3][col/3][num]=true;}}}return true;}
};

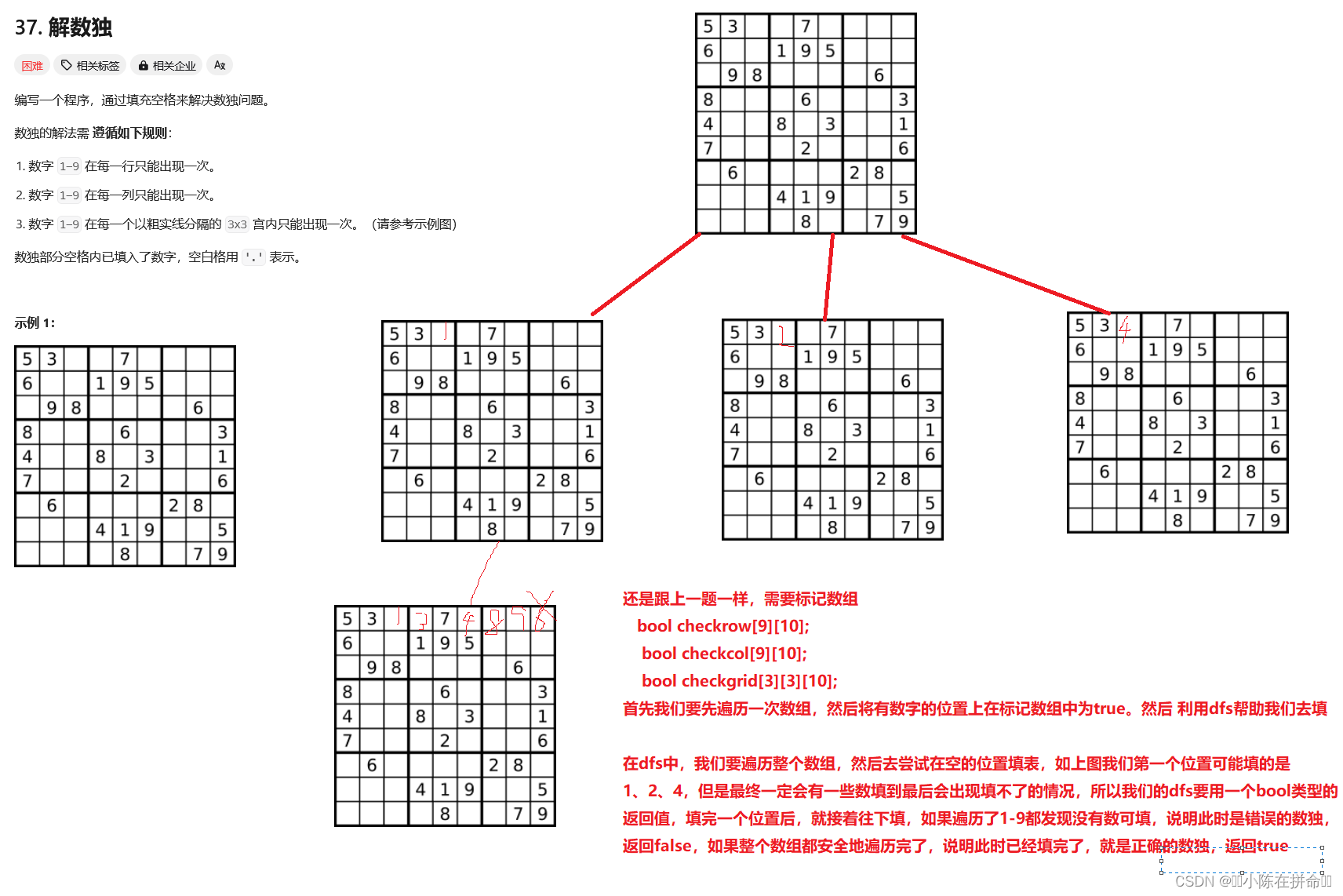
三、解数独

. - 力扣（LeetCode）

class Solution {
public:bool checkrow[9][10];bool checkcol[9][10];bool checkgrid[3][3][10];void solveSudoku(vector<vector<char>>& board) {//初始化for(int row=0;row<9;++row)for(int col=0;col<9;++col){if(board[row][col]!='.'){int num=board[row][col]-'0';checkrow[row][num]=checkcol[col][num]=checkgrid[row/3][col/3][num]=true;}}dfs(board);}bool dfs(vector<vector<char>> &board)//bool用来告诉上一层决策是正确的{for(int row=0;row<9;++row)for(int col=0;col<9;++col){if(board[row][col]=='.'){//开始尝试填数for(int num=1;num<=9;++num){if(!checkrow[row][num]&&!checkcol[col][num]&&!checkgrid[row/3][col/3][num]){//说明能填，就填上board[row][col]=num+'0';checkrow[row][num]=checkcol[col][num]=checkgrid[row/3][col/3][num]=true;if(dfs(board)) return true;//去下一个位置填，如果填成功了，返回true//恢复现场board[row][col]='.';checkrow[row][num]=checkcol[col][num]=checkgrid[row/3][col/3][num]=false;}}return false;//1-9没有一个数能填，说明决策错误}}return true;//安全地填完了，返回true}
};

四、单词搜索

. - 力扣（LeetCode）

class Solution {
public:bool check[6][6];//用来标记选过的位置int m,n;vector<vector<char>> board;string word;bool exist(vector<vector<char>>& _board, string _word) {board=_board;word=_word;m=board.size();n=board[0].size();for(int i=0;i<m;++i)for(int j=0;j<n;++j){if(board[i][j]==word[0]){check[i][j]=true;if(dfs(i,j,1))  return true;check[i][j]=false;}}return false;}//用向量的方式来定义int dx[4]={0,0,-1,1};int dy[4]={1,-1,0,0}; //就可以将4个方向改变成一个for循环bool dfs(int i,int j,int pos){if(pos==word.size())  return true;for(int k=0;k<4;++k){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&check[x][y]==false&&board[x][y]==word[pos]){check[x][y]=true;if(dfs(x,y,pos+1)) return true;check[x][y]=false;}}return false;//如果四个方向都找不到，说明确实没有可填的数，直接返回}
};

五、黄金旷工

. - 力扣（LeetCode）

class Solution {
public:int ret=0;bool check[15][15];int m,n;int getMaximumGold(vector<vector<int>>& grid) {m=grid.size();n=grid[0].size();for(int i=0;i<m;++i)for(int j=0;j<n;++j){if(grid[i][j]){check[i][j]=true;dfs(grid,i,j,grid[i][j]);check[i][j]=false;}}return ret;}//用向量的方式来定义int dx[4]={0,0,-1,1};int dy[4]={1,-1,0,0}; //就可以将4个方向改变成一个for循环void dfs(vector<vector<int>>& grid,int i,int j,int count){for(int k=0;k<4;++k){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&!check[x][y]&&grid[x][y]){check[x][y]=true;dfs(grid,x,y,count+grid[x][y]);check[x][y]=false;}}ret=max(count,ret);//for循环结束，确实没得填了，更新}
};

六、不同路径III

. - 力扣（LeetCode）

class Solution {
public:int ret;bool check[20][20];//用来标记int m,n,step;//step用来统计可以走的方格个数int uniquePathsIII(vector<vector<int>>& grid) {ret=0;m=grid.size();n=grid[0].size();step=0;int bx=0,by=0;//记录起点//先找起点for(int i=0;i<m;++i)for(int j=0;j<n;++j){if(grid[i][j]==0) ++step;else if(grid[i][j]==1) {bx=i;by=j;}}step+=2;//把起点和终点算上，最后走到终点的时候就可以返回了check[bx][by]=true;dfs(grid,bx,by,1);return ret;}int dx[4]={0,0,-1,1};int dy[4]={1,-1,0,0}; //就可以将4个方向改变成一个for循环void dfs(vector<vector<int>>& grid,int i,int j,int count){if(grid[i][j]==2&&count==step) {++ret;return;}for(int k=0;k<4;++k){int x=i+dx[k],y=j+dy[k];if(x>=0&&x<m&&y>=0&&y<n&&!check[x][y]&&grid[x][y]!=-1){check[i][j]=true;dfs(grid,x,y,count+1);check[i][j]=false;}}}
};