深度学习框架的张量

张量的运算是深度学习的核心，如一张图片可以看作是四维的张量，一个迷你批次的文本可以看作是二维张量，基本上所有的深度学习模型都可以表示为张量的操作，梯度、反向传播算法也可以表示为张量和张量的运算

张量在内存中的排列方式是连续的，而且是从最后一个维度开始排列

张量的性质

1. 在深度学习中，张量应该能够支持得到每一个维度的长度，也就是保存张量的形状
2. 张量需要支持和其他相同类型的张量的加减乘除运算
3. 张量还应该支持变形，也就是说，张量可以变换为总元素的数目相同，但是维度不同的另一个张量——可以将一个张量的某个维度分割为两个维度，或者将最后几个维度合并为一个维度。由于变形之前的两个张量的分量在内存中的排列形状一定是相同的，所以，这两个张量一般会在内存的底层哦女相同一个内存区域
4. 张量应当支持线性变换（如在卷积层和全连接层中进行的运算）和对每个元素的激活函数进行操作，实现线性变换和激活函数的操作是为了能够方便地进行神经网络的前向运算

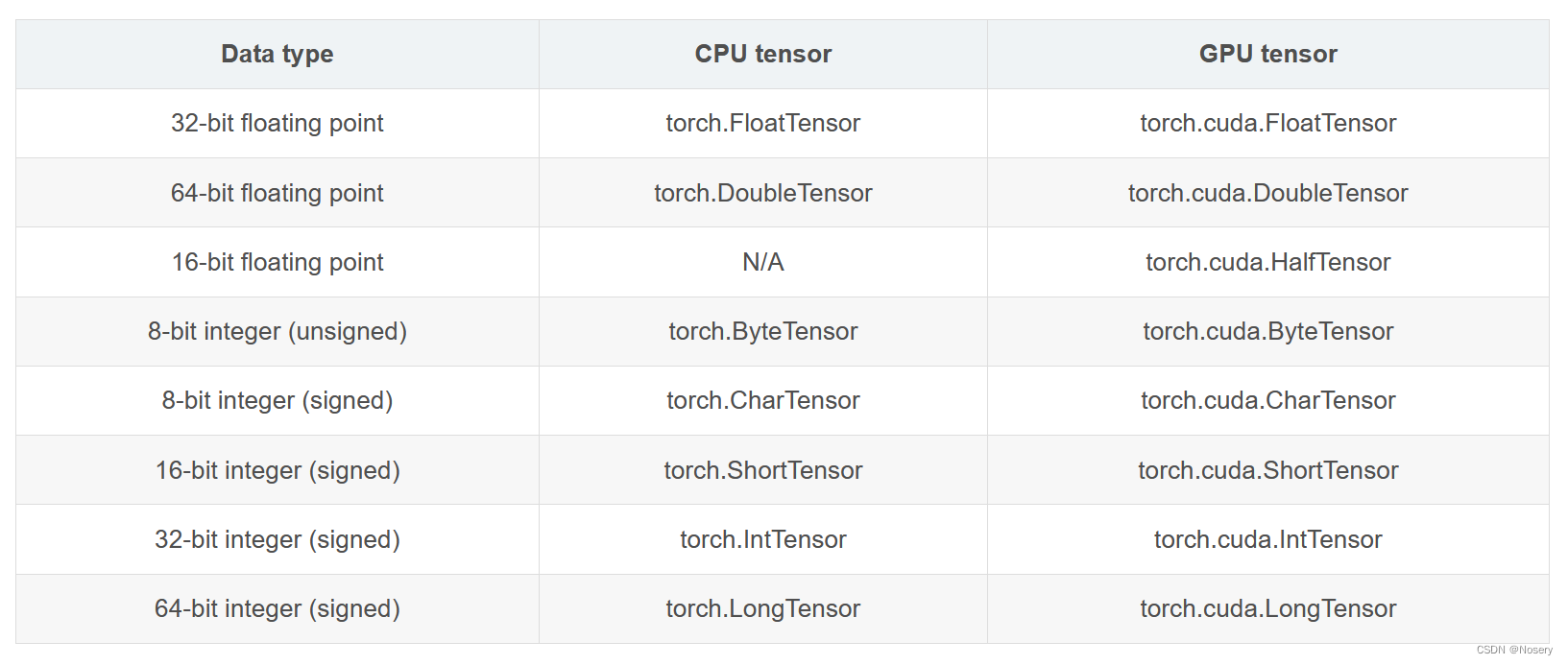
Pytorch的张量一共支持9种数据类型，每种数据类型都对应CPU和GPU的两种子类型——如果要获取一个张量的具体类型，可以直接访问张量的dtype属性，如果想要进一步获取张量的存储位置和数据类型，可以通过调用张量的type方法来同时获取存储位置和数据类型的值

现阶段Pytorch并不支持负数类型，如果有要用到的场合，需要使用张量的两个分量来分别模拟负数的实部和虚部，不同的类型之间，可以通过调用to方法进行转换，该方法传入的参数是转换目标类型

张量的创建方式

在Pytorch中创建张量的方式主要有四种方式：

torch.Tensor()、torch.tensor()、torch.as_tensor()、torch.from_numpy()

Pytorch创建张量的四种函数方法及其区别_python_脚本之家

pytorch中8种特殊张量创建方法_pytorch创建-CSDN博客

PyTorch ： 了解Tensor(张量)依据数值和概率的创建方法 - 知乎

张量的存储设备

pytorch的张量可以在两种设备上创建：CPU和GPU

通过访问张量的device属性可以获取张量所在的设备，在没有指定设备的时候，pytorch会默认存储张量到CPU上面，如果要想转移到GPU上面，则需要指定张量转移到GPU设备：首先可以使用cpu方法把张量转移到CPU上，其次可以使用cuda方法把张量转移到GPU上，其中需要传入具体的GPU的设备编号；也可以使用to方法把张量从一个设备转移到另一个设备上面，该方法的参数是目标设备的名称（可以使字符串名称，也可以是torch.device实例）

PyTorch 将 PyTorch 代码从 CPU 移植到 GPU|极客笔记

需要注意的是——两个或多个张量之间的运算只有在相同的设备上才能运行（都在CPU或GPU上面），否则就会报错

和张量维度相关的方法

在深度学习中常会用到一些方法获取张量的维度数目，以及某一维度的具体大小，或者对张量的某些维度进行操作

tensor / numpy维度变换操作总结_np维度调换-CSDN博客

张量的运算

涉及单个张量的函数运算

深度学习中，常会用到对张量作四则运算、线性变换和激活等，这些方法可以由张量自带的方法实现，也可以由torch包中的一些函数实现

1、张量的四则运算

import torch  # 创建两个张量  
tensor1 = torch.tensor([1.0, 2.0, 3.0])  
tensor2 = torch.tensor([4.0, 5.0, 6.0])  # 加法  
addition = tensor1 + tensor2  
print("加法:", addition)  # 减法  
subtraction = tensor1 - tensor2  
print("减法:", subtraction)  # 乘法  
multiplication = tensor1 * tensor2  
print("乘法:", multiplication)  # 除法  
division = tensor1 / tensor2  
print("除法:", division)

2、线性变换

线性变换通常通过矩阵乘法实现。在PyTorch中，可以使用mm（针对二维张量）或matmul（针对任意维度的张量）进行矩阵乘法

# 创建一个二维张量（矩阵）  
matrix = torch.tensor([[1.0, 2.0], [3.0, 4.0]])  # 创建一个向量  
vector = torch.tensor([5.0, 6.0])  # 矩阵乘法  
linear_transformation = torch.matmul(matrix, vector.view(-1, 1))  
print("线性变换:", linear_transformation)

3、激活函数

激活函数是神经网络中非常重要的组成部分，它们为模型引入了非线性。PyTorch提供了许多内置的激活函数

# 创建一个张量  
input_tensor = torch.tensor([-2.0, 0.0, 2.0])  # 使用ReLU激活函数  
relu_output = torch.relu(input_tensor)  
print("ReLU激活:", relu_output)  # 使用Sigmoid激活函数  
sigmoid_output = torch.sigmoid(input_tensor)  
print("Sigmoid激活:", sigmoid_output)

在实际的深度学习模型中，这些操作会组合在一起，形成复杂的神经网络结构

涉及多个张量的函数方法

在深度学习中，经常需要对两个形状相同的张量进行逐个元素的四则运算。这些操作都是逐元素的，意味着张量中对应位置的元素会分别进行加法、减法、乘法或除法运算。在PyTorch中，这些操作可以通过简单的运算符重载实现

import torch  # 创建两个形状相同的张量  
tensor1 = torch.tensor([[1.0, 2.0], [3.0, 4.0]])  
tensor2 = torch.tensor([[5.0, 6.0], [7.0, 8.0]])  # 逐个元素的加法  
addition = tensor1 + tensor2  
print("加法:", addition)  # 逐个元素的减法  
subtraction = tensor1 - tensor2  
print("减法:", subtraction)  # 逐个元素的乘法  
multiplication = tensor1 * tensor2  
print("乘法:", multiplication)  # 逐个元素的除法  
# 注意：除法运算需要确保分母不为0，否则会导致错误或无穷大的结果  
division = tensor1 / tensor2  
print("除法:", division)  # 对于除法，如果担心分母为0，可以使用clamp函数确保分母不会太小  
tensor2_clamped = tensor2.clamp(min=1e-6)  # 设置一个小的正数作为分母的最小值  
safe_division = tensor1 / tensor2_clamped  
print("安全的除法:", safe_division)

还可以通过add、sub、mul、div方法来实现，同样也可以通过内置方法的原地操作版本实现

import torch  # 创建两个形状相同的张量  
tensor1 = torch.tensor([[1.0, 2.0], [3.0, 4.0]])  
tensor2 = torch.tensor([[5.0, 6.0], [7.0, 8.0]])  # 使用add方法实现加法  
addition = tensor1.add(tensor2)  
print("加法:", addition)  # 使用sub方法实现减法  
subtraction = tensor1.sub(tensor2)  
print("减法:", subtraction)  # 使用mul方法实现乘法  
multiplication = tensor1.mul(tensor2)  
print("乘法:", multiplication)  # 使用div方法实现除法  
# 注意：同样需要确保分母不为0  
division = tensor1.div(tensor2)  
print("除法:", division)  # 原地操作版本，直接在原张量上修改  
# 注意：原地操作不会返回新的张量，而是修改原张量  
result = tensor1.clone()  # 复制tensor1以便进行原地操作  
result.add_(tensor2)     # 原地加法  
print("原地加法结果:", result)  result = tensor1.clone()  # 再次复制tensor1  
result.sub_(tensor2)     # 原地减法  
print("原地减法结果:", result)  result = tensor1.clone()  
result.mul_(tensor2)     # 原地乘法  
print("原地乘法结果:", result)  result = tensor1.clone()  
result.div_(tensor2)     # 原地除法  
print("原地除法结果:", result)

张量的极值和排序

深度学习中，我们常需要获取张量的最大值和最小值，以及这些值所在的位置，如果只需要最大值和最小值，可以使用argmax和argmin，通过传入具体要沿着那个维度求最大值和最小值的位置，返回沿着该维度最大和最小值对应的序号是多少，如果既要求获取最大值和最小值，又要求获得具体的值，就需要使用max和min，通过传入具体的维度，同时返回沿着该维度最大和最小值的位置，以及对应的最大值和最小值组成的元组

最后一个和大小有关的函数是排序函数sort（默认是从小到大，如果需要从大到小排序，则需要设置参数 descending=True），同样是传入具体需要进行排序的维度，返回的是排序完的张量，记忆对应排序后的元素在原始张量上的位置，如果要知道原始张量还是那的元素沿着某个维度排第几位，只需要对应排序后的元素在原始张量上的位置进行再次排序，得到新位置的值即为原始张量沿着搞方向进行大小排序后的序号，和前面一样，关于排序和极值的函数，既可以是Pytorch的函数，也可以是张量的内置方法，两种方法的调用方法等价

import torch  # 创建一个张量  
tensor = torch.tensor([[4.0, 2.0, 9.0], [6.0, 5.0, 3.0], [8.0, 1.0, 7.0]])  # 使用argmax获取最大值的位置  
max_indices = tensor.argmax(dim=1)  # 沿着维度1（列）查找最大值的位置  
print("最大值的位置:", max_indices)  # 使用argmin获取最小值的位置  
min_indices = tensor.argmin(dim=1)  # 沿着维度1（列）查找最小值的位置  
print("最小值的位置:", min_indices)  # 使用max获取最大值及其位置  
max_values, max_positions = tensor.max(dim=1)  # 沿着维度1（列）查找最大值及其位置  
print("最大值和它们的位置:", max_values, max_positions)  # 使用min获取最小值及其位置  
min_values, min_positions = tensor.min(dim=1)  # 沿着维度1（列）查找最小值及其位置  
print("最小值和它们的位置:", min_values, min_positions)  # 使用sort对张量进行排序  
sorted_tensor, sorted_indices = tensor.sort(dim=1, descending=False)  # 从小到大排序，并获取原始位置的索引  
print("排序后的张量:", sorted_tensor)  
print("排序后的元素在原始张量上的位置:", sorted_indices)  # 如果要知道原始张量中的元素沿着某个维度排第几位，需要对排序后的索引进行排序  
original_indices = torch.arange(sorted_indices.size(0)).to(sorted_indices.device)  # 创建原始索引  
sorted_original_indices = sorted_indices.argsort(dim=1)  # 对排序后的索引进行排序  
print("原始张量元素排序后的序号:", sorted_original_indices)

矩阵的乘法和张量的缩并

除上述的运算之外，由两个张量作为参数的操作还有矩阵乘法（线性变换），可以使用torch.mm函数或者张量内置的mm方法进行矩阵乘法，还可以使用@运算符实现

需要注意的是，如果你的张量不是二维的（例如，它们包含额外的维度，如批次维度），你可能需要使用torch.matmul函数或matmul方法，或者使用@运算符（在PyTorch中，@运算符在内部实际上是调用torch.matmul）。torch.matmul可以处理任意维度的张量，只要它们的维度是兼容的以进行矩阵乘法

import torch  # 创建两个二维张量（矩阵）  
matrix1 = torch.tensor([[1.0, 2.0], [3.0, 4.0]])  
matrix2 = torch.tensor([[5.0, 6.0], [7.0, 8.0]])  # 使用torch.mm函数进行矩阵乘法  
result_mm = torch.mm(matrix1, matrix2)  
print("使用torch.mm的结果:", result_mm)  # 使用张量内置的mm方法进行矩阵乘法  
result_method = matrix1.mm(matrix2)  
print("使用张量mm方法的结果:", result_method)  # 使用@运算符进行矩阵乘法  
result_at = matrix1 @ matrix2  
print("使用@运算符的结果:", result_at)

另一个特殊的矩阵乘法的函数是bmm函数，在深度学习中，实际经常用到的数据是迷你批次的数据，一般来说，第一个维度是迷你批次的大小，因此，数据的矩阵实际上是一个迷你批次的矩阵，即一个三维的张量（可以看作是一个迷你批次数量和矩阵叠加在一起）

此时如果两个张量做矩阵乘法，一般情况下是沿着迷你批次的方向分别对每个矩阵对做乘法，最后把结果整合在一起，如果是一个 b×m×k 的张量和 b×k×n 的张量相乘，那么结果应该是 b×m×n 的张量，torch.einsum 函数的使用如下

torch.einsum 是一个极其强大的函数，它用于在 PyTorch 中执行爱因斯坦求和约定（Einstein summation convention）。爱因斯坦求和约定提供了一种紧凑的方式来表示多维数组（如张量）之间的复杂操作，包括但不限于点积、外积、转置、矩阵乘法、批量矩阵乘法等。

torch.einsum 的基本语法是：

torch.einsum(equation, *operands)

其中 equation 是一个描述操作的字符串，而 *operands 是参与操作的张量列表。

Einstein Summation Convention 的基本思想

爱因斯坦求和约定使用特定的标记来表示张量的维度，并通过省略号来指定对这些维度进行求和。

• 字母（如 i, j, k, ...）表示张量的维度。
• 每个字母在每个张量中最多出现两次：一次在输入位置，一次在输出位置。
• 如果一个字母在输出位置没有出现，则意味着对该维度进行求和。
• 省略号 ... 用于表示多个维度。

示例

1. 向量点积

import torch a = torch.tensor([1.0, 2.0, 3.0]) 
b = torch.tensor([4.0, 5.0, 6.0]) result = torch.einsum('i,i->', a, b) # 点积：1*4 + 2*5 + 3*6 
print(result) # 输出：32.0

2. 矩阵乘法

A = torch.tensor([[1.0, 2.0], [3.0, 4.0]]) 
B = torch.tensor([[5.0, 6.0], [7.0, 8.0]]) result = torch.einsum('ij,jk->ik', A, B) # 矩阵乘法 
print(result)

3. 批量矩阵乘法

A = torch.randn(3, 2, 5) # 3个2x5矩阵 
B = torch.randn(3, 5, 4) # 3个5x4矩阵 result = torch.einsum('bij,bjk->bik', A, B) # 批量矩阵乘法，输出为3个2x4矩阵 
print(result.shape) # 输出：torch.Size([3, 2, 4])

4. 转置

M = torch.randn(2, 3) # 转置矩阵，从 'ij' 变为 'ji' 
transposed = torch.einsum('ij->ji', M) 
print(transposed)

5. 外积

a = torch.tensor([1.0, 2.0]) 
b = torch.tensor([3.0, 4.0]) # 外积，输出是一个2x2的矩阵 
outer_product = torch.einsum('i,j->ij', a, b) 
print(outer_product)

torch.einsum 的强大之处在于它可以以非常简洁的方式表达复杂的张量操作，而不需要编写冗长的循环或显式的维度操作代码。这使得它在处理高维数据和复杂的神经网络结构时特别有用

张量的拼接和分割

在PyTorch中，你可以使用torch.cat来拼接张量，使用torch.chunk、torch.split或torch.narrow等函数来分割张量。下面是一些代码示例：

张量的拼接

假设我们有两个形状相同的张量，我们想要将它们沿某个维度拼接起来

import torch # 创建两个形状相同的张量 
tensor1 = torch.tensor([[1, 2], [3, 4]]) 
tensor2 = torch.tensor([[5, 6], [7, 8]]) # 沿着第一个维度（行）拼接 
concatenated_row = torch.cat((tensor1, tensor2), dim=0) 
print("沿着行拼接：") 
print(concatenated_row) # 沿着第二个维度（列）拼接 
concatenated_col = torch.cat((tensor1, tensor2), dim=1) 
print("沿着列拼接：") 
print(concatenated_col)

张量的分割

分割张量通常涉及到将一个大张量分成若干个小张量。

使用torch.chunk分割张量

torch.chunk函数将张量分割成指定数量的块

# 创建一个张量 
tensor = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) # 沿着第一个维度（行）分割成2块 
chunks_row = torch.chunk(tensor, chunks=2, dim=0) 
for chunk in chunks_row: 
print(chunk) # 沿着第二个维度（列）分割成2块 
chunks_col = torch.chunk(tensor, chunks=2, dim=1) 
for chunk in chunks_col: 
print(chunk)

使用torch.split分割张量

torch.split函数允许你按照更灵活的规则分割张量，可以指定每个块的大小

# 创建一个张量 
tensor = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) # 沿着第二个维度（列）分割，指定每个块的大小 
split_col = torch.split(tensor, split_size_or_sections=[2, 1, 1], dim=1) 
for part in split_col: 
print(part)

使用torch.narrow选择张量的狭窄切片

torch.narrow不是用来分割张量的，但它可以用来选择张量沿着某一维度的一个狭窄切片

# 创建一个张量 
tensor = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) # 选择第二行 
narrow_tensor = tensor.narrow(0, 1, 1) 
print(narrow_tensor) # 选择第一列到第三列 
narrow_tensor_col = tensor.narrow(1, 0, 3) 
print(narrow_tensor_col)

注意：上述代码中torch.cat函数的括号使用有误，正确的应该是去掉内层的括号。修正后的代码应该如下所示：

# 沿着第一个维度（行）拼接 
concatenated_row = torch.cat((tensor1, tensor2), dim=0) # 错误用法 
concatenated_row = torch.cat((tensor1, tensor2), dim=0) # 正确用法，但内层括号是多余的 
concatenated_row = torch.cat([tensor1, tensor2], dim=0) # 更常见的正确用法 # 沿着第二个维度（列）拼接 
concatenated_col = torch.cat((tensor1, tensor2), dim=1) # 错误用法 
concatenated_col = torch.cat([tensor1, tensor2], dim=1) # 正确用法

在实际使用中，通常更推荐使用列表[]来传递要拼接的张量，而不是元组()，尽管在某些情况下元组也是可行的

张量维度的扩增和压缩

在PyTorch中，张量维度的扩增（也称为扩展或广播）和压缩是常见的操作。这通常通过torch.unsqueeze和torch.squeeze函数实现。此外，torch.shape、torch.view和torch.flatten等函数也常用于改变张量的形状

张量维度的扩增（Unsqueeze）

torch.unsqueeze函数用于在张量的指定位置增加一个新的维度，大小为1

import torch # 创建一个形状为 [2, 3] 的张量 
tensor = torch.tensor([[1, 2, 3], [4, 5, 6]]) 
print("原始张量:") 
print(tensor) 
print("形状:", tensor.shape) # 在第一个维度前增加一个新维度 
tensor_unsqueezed_dim0 = torch.unsqueeze(tensor, dim=0) 
print("在第一个维度前增加维度后的张量:") 
print(tensor_unsqueezed_dim0) 
print("形状:", tensor_unsqueezed_dim0.shape) # 在第二个维度后增加一个新维度 
tensor_unsqueezed_dim1 = torch.unsqueeze(tensor, dim=1) 
print("在第二个维度后增加维度后的张量:") 
print(tensor_unsqueezed_dim1) 
print("形状:", tensor_unsqueezed_dim1.shape)

张量维度的压缩（Squeeze）

torch.squeeze函数用于移除张量中所有大小为1的维度

# 使用上面的 tensor_unsqueezed_dim1 张量，它有一个大小为1的维度在第二个位置 
print("带有一个大小为1的维度的张量:") 
print(tensor_unsqueezed_dim1) 
print("形状:", tensor_unsqueezed_dim1.shape) # 压缩大小为1的维度 
tensor_squeezed = torch.squeeze(tensor_unsqueezed_dim1) 
print("压缩维度后的张量:") 
print(tensor_squeezed) 
print("形状:", tensor_squeezed.shape)

重塑张量形状（Reshape/View）

torch.resape和torch.view函数用于改变张量的形状，但不改变数据

# 使用原始的 [2, 3] 张量 
print("原始张量:") 
print(tensor) 
print("形状:", tensor.shape) # 使用reshape改变形状为 [3, 2] 
tensor_reshaped = tensor.reshape(3, 2) 
print("重塑后的张量:") 
print(tensor_reshaped) 
print("形状:", tensor_reshaped.shape) # 使用view改变形状为 [6] 
tensor_view = tensor.view(6) 
print("view后的张量:") 
print(tensor_view) 
print("形状:", tensor_view.shape)

请注意，reshape和view要求新形状与原始张量的元素总数相同。如果尝试将张量重塑为不兼容的形状，将会引发错误

张量展平（Flatten）

展平张量意味着将其所有维度合并成一个维度，通常用于将多维张量转换为一维张量

# 使用原始的 [2, 3] 张量 
print("原始张量:") 
print(tensor) 
print("形状:", tensor.shape) # 使用flatten展平张量 
tensor_flattened = tensor.flatten() 
print("展平后的张量:") 
print(tensor_flattened) 
print("形状:", tensor_flattened.shape)

torch.flatten函数还允许你指定从哪一维度开始展平以及是否保持批处理维度。这对于处理具有批处理维度的张量（如在神经网络中）特别有用

张量的广播

在PyTorch中，广播（broadcasting）是一种强大的机制，它允许PyTorch在元素级操作中对不同形状的张量进行自动扩展。这允许你在不显式重塑张量的情况下执行诸如加法、乘法等操作。广播规则基于NumPy的广播规则

import torch  # 创建两个形状不同的张量  
tensor1 = torch.tensor([[1, 2, 3]])  # 形状: [1, 3]  
tensor2 = torch.tensor([[4], [5], [6]])  # 形状: [3, 1]  # 由于广播规则，我们可以直接对这两个张量进行加法操作  
# tensor1 会沿着第0维（行）复制以匹配tensor2的形状  
# tensor2 会沿着第1维（列）复制以匹配tensor1的形状  
# 结果形状为 [3, 3]  
result = tensor1 + tensor2  print("tensor1:")  
print(tensor1)  
print("形状:", tensor1.shape)  print("tensor2:")  
print(tensor2)  
print("形状:", tensor2.shape)  print("广播后的结果:")  
print(result)  
print("形状:", result.shape)

在上面的例子中，tensor1 的形状是 [1, 3]，而 tensor2 的形状是 [3, 1]。当我们将这两个张量相加时，PyTorch会根据广播规则自动扩展它们以匹配对方的形状。具体来说，tensor1 会在第0维（行）上复制以匹配 tensor2 的3行，而 tensor2 会在第1维（列）上复制以匹配 tensor1 的3列。因此，结果张量的形状是 [3, 3]。

广播规则要求，从右到左比较每个维度的大小：

1. 如果两个维度的大小相等，或者其中一个维度的大小为1，则它们兼容，因此可以进行广播。
2. 如果两个维度的大小都不为1且不相等，则它们不兼容，无法广播。

在上述例子中，tensor1 的第1维（列）大小为3，而 tensor2 的第0维（行）大小为3，因此它们是兼容的。同时，tensor1 的第0维（行）大小为1，而 tensor2 的第1维（列）大小为1，因此它们也是兼容的。因此，这两个张量可以广播