leetcode 热题 100
双指针
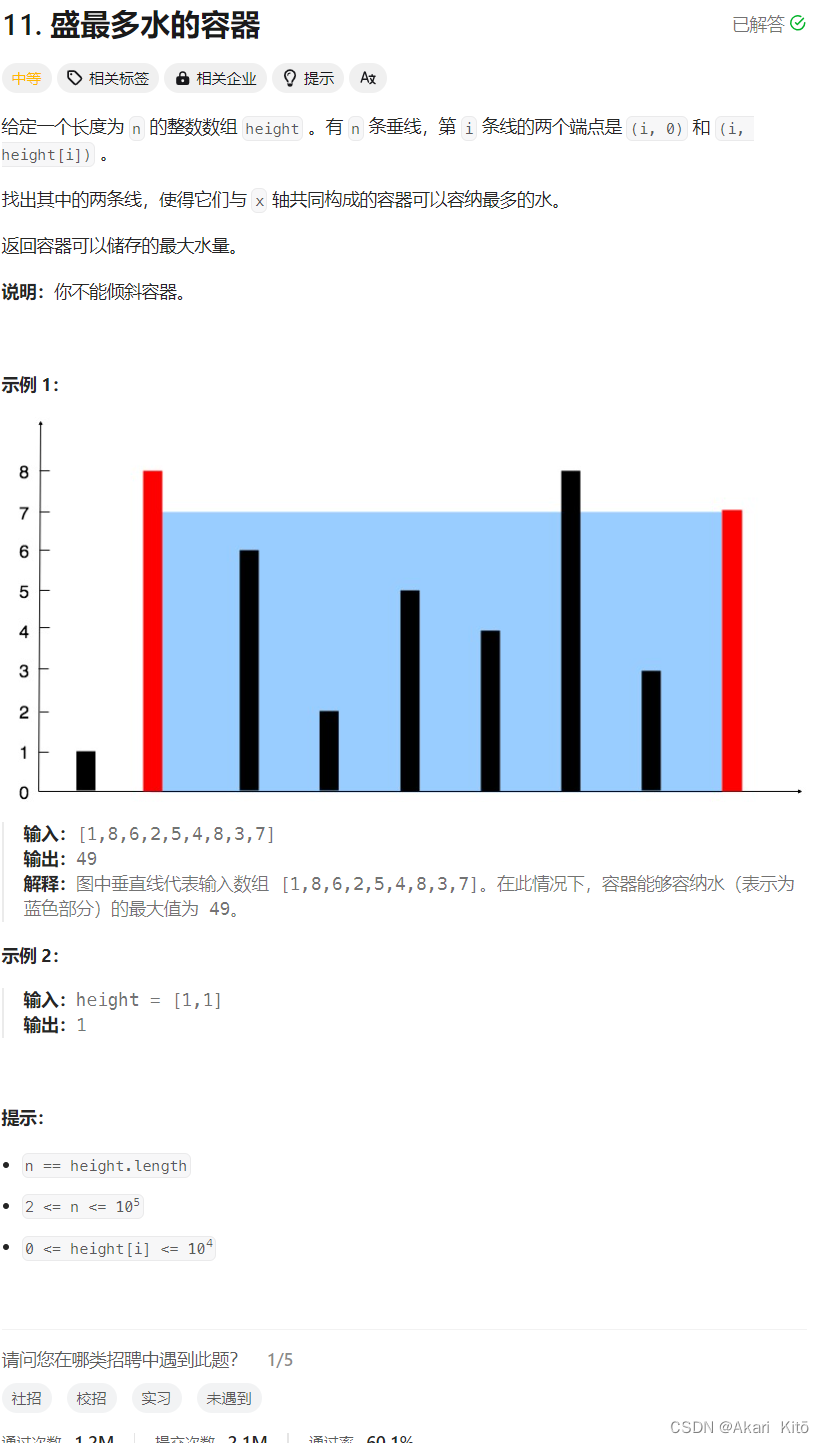
盛最多水的容器 【mid】【双指针】
思路:
好久没写代码sb了,加上之前写的双指针并不多,以及有点思维定势了。我对双指针比较刻板的印象一直是两层for循环i,j,初始时i,j都位于左界附近,但是对于第i次的内层循环,j只需要从第i-1次内层循环停下时的j开始循环,即内层的循环变量j一直在增加,而不会减少,故双指针复杂度O(n)。
然鹅,本题利用双指针l,r,初始分别位于左界和右界,之后++l和--r,这样子移动。
至于如何移动,写出容器容量公式便很容易想出V=(r - l - 1) * min(height[l], height[r])。为取得Vmax,考虑无论移动l or r,都会使得宽d = r - l - 1 变小,故考虑如何使得min(height[l], height[r])变大,容易发现应该移动height小的那一个。
AC代码
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int l = 0, r = n - 1;int s = (r - l) * min(height[l], height[r]);int res = s;while(l < r){if(height[l] < height[r]) ++l;else --r;s = (r - l) * min(height[l], height[r]);res = max(res, s);}return res;}
};
三数之和 【mid】【双指针】

思路:
与上一题类似。
先排序,之后搜一遍。
对于nums[i],需要从右边找出两个数字使得和为-nums[i]。
双指针l,r初始分别为左界和右界,据nums[l] + nums[r]与-nums[i]的大小关系决定移动哪个指针即可。
另外对于去重,可直接通过set逃课。
AC代码
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {int n = nums.size();vector<vector<int>> res;set<vector<int>> st;sort(nums.begin(), nums.end());int a, sum, last = -5000000;int l, r;bool flag;for(int i = 0; i < n; ++i){if(nums[i] == last) continue;else{last = nums[i];l = i + 1; r = n - 1;a = -nums[i];while(l < r){sum = nums[l] + nums[r];if(sum > a) --r;else if(sum < a) ++l;else {vector<int> vt;vt.push_back(nums[i]);vt.push_back(nums[l]);vt.push_back(nums[r]);st.insert(vt);++l;}}}}for(auto x : st) res.push_back(x);return res;}
};
接雨水【hard】【双指针/单调栈】

思路:
【解1】:预处理(对应官方题解dp解法)
考虑每个洼地可容纳的雨水,取决于这个洼地左侧和右侧的最高的高地的较小值。对于每个洼地左侧和右侧的最高的高地,预处理即可。
【解2】:双指针
思路同解1,只不过不做预处理,而是用双指针l,r初始分别为左界右界,移动过程中,分别维护扫过区域的最大值,每次移动最大值较小的那一侧,然后判断移动之后是洼地还是高地,洼地则计算接的雨水,高地则更新单侧最大值。
关于为什么移动最大值较小的那一侧,假设较高的一侧是r。
移动r侧,由于移动之后可能是高地or洼地,对于高地,不计算贡献,其实无所谓,但是对于洼地,需要计算贡献,此时贡献取决于洼地两侧最高的高地的较小值,然而左侧最高的高地其实是不确定的,故无法计算。倘若移动是l的一侧,虽然右侧最高的高地也是不确定的,但至少可以确定的是右侧的高地一定比左侧的高,故可以计算正确的贡献。
【解3】:单调栈
构造一个单减栈(栈底>栈顶)。对于单调栈,其实每个元素都会进栈一次。
对于遍历到的当前元素,若<栈顶元素,入栈
否则,说明存在可以积水的洼地,此时需要弹出栈顶元素,可积的雨水取决于洼地的宽度(据两侧高地的距离)及可积雨水的高地,循环处理,直至当前元素可以入栈。(此过程官方视频题解动画容易理解)。
AC代码:
预处理:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;int lmx[n + 5], rmx[n + 5];lmx[0] = height[0], rmx[n - 1] = height[n - 1];for(int i = 1; i < n; ++i) lmx[i] = max(lmx[i - 1], height[i]);for(int i = n - 2; i >= 0; --i) rmx[i] = max(rmx[i + 1], height[i]); int mx1, mx2, h;for(int i = 0; i < n; ++i){mx1 = lmx[i], mx2 = rmx[i];h = min(mx1, mx2);res += (h - height[i]);}return res;}
};
双指针:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;int l = 0, r = n - 1;int lmx = height[0], rmx = height[n - 1];while(l < r){if(lmx < rmx){++l;if(lmx > height[l]) res += lmx - height[l];else lmx = height[l];}else{--r;if(rmx > height[r]) res += rmx - height[r];else rmx = height[r];}}return res;}
};
单调栈:
class Solution {
public:int trap(vector<int>& height) {stack<int> st;int n = height.size();int res = 0;for(int i = 0; i < n; ++i){while(!st.empty() && height[i] > height[st.top()]){int tp = st.top();st.pop();if(st.empty()) break;int l = st.top();int d = i - l - 1;int h = min(height[l], height[i]) - height[tp];res += d * h;}st.push(i);}return res;}
};
子串
最小覆盖字串【hard】【双指针/滑动窗口】

思路:
先找出左边界为字符串s的左边界且能覆盖t的最小子串。
之后,利用双指针/滑动窗口的思想,交替移动左右指针l,r
具体规则如下:
若当前子串能够覆盖,则++l,否则++r,每次移动后判断新的子串是否能够覆盖并且是否变小,保存最小能覆盖的子串长度以及其左右边界l,r。
关于如何判断,只需在移动的过程中维护好如下容器or变量便显而易见。
map<char, int> mp; //hash,'a'~'z'对应1~26,'A'~'Z'对应27~52
int cnt_s[64] //cnt_s[i]表示当前子串s[l~r]中i对应的字母个数,cnt_t[i]表示
int cnt_t[64]; //cnt_t[i]表示t串中i对应的字母一共有几个
int num = 0, cnt = 0; //num表示t串一共有多少个不同的字母,cnt表示当前子串s[l~r]已经覆盖了t中的字母个数
int l, r; //当前正在处理的子串s[l~r]
int min_l, min_r, mi = inf; //目前所有处理的子串中能覆盖的最小子串的左右边界及长度
AC代码:
class Solution {
public:string minWindow(string s, string t) {const int inf = 0x3f3f3f3f;int len1 = s.size(), len2 = t.size();map<char, int> mp;int cnt_s[64], cnt_t[64];int num = 0, cnt = 0;int l, r, min_l = 0, min_r = 0, mi = inf; string str;for(char ch = 'a'; ch <= 'z'; ++ch) mp[ch] = ch - 'a' + 1;for(char ch = 'A'; ch <= 'Z'; ++ch) mp[ch] = ch - 'A' + 1 + 26;for(int i = 0; i < len2; ++i) ++cnt_t[mp[t[i]]];for(int i = 1; i < 55; ++i) if(cnt_t[i]) ++num;l = 0, r = -1;while(r < len1){if(cnt == num){if(cnt_s[mp[s[l]]] == cnt_t[mp[s[l]]]) --cnt;--cnt_s[mp[s[l++]]];}else{++cnt_s[mp[s[++r]]];if(cnt_s[mp[s[r]]] == cnt_t[mp[s[r]]]) ++cnt;}if(cnt == num && r - l + 1 < mi){mi = r - l + 1;min_l = l, min_r = r;} }if(mi == inf) return "";else {str = s.substr(min_l, mi);return str;}}
};
普通数组
轮转数组【mid】【数论/gcd】

思路
给出空间O(1),且不用reverse的方法。(官方题解推导比较清楚)。
维护两个变量pos和tmp,分别表示现在的位置和对应位置上的值,由此,更新只需pos = (pos + k) % n,swap(nums[pos], tmp),当pos回到最开始的位置时,我们称这是完成了一趟修改,此时应该停下,然鹅有的元素并没有遍历到。(只将下标为gcd(k,n)的元素遍历了,可证,另见类似题目,2015ICPC沈阳,跳青蛙🐸容斥),故需要将pos+1,再依次为开始,继续上述操作,直至回到开始位置并遍历全部位置。
接下来考虑需要几趟(根据上面结论,其实可知需要gcd(n,k)趟)。假设转了a圈,遍历了b个元素,则an=bk,故an一定是n,k的倍数,又因为我们在第一次回到起点时便结束了,故a应尽可能的小,由此an=lcm(n,k),故b=lcm(n,k)/k,即需要遍历的趟数cnt=n/b=gcd(n,k)。
AC代码:
class Solution {
public:int gcd(int a, int b){return b == 0 ? a : gcd(b, a % b);}void rotate(vector<int>& nums, int k) {int n = nums.size();k %= n;int cnt = gcd(n, k);for(int i = 0; i < cnt; ++i){int pos = i;int tmp = nums[i];while(true){pos = (pos + k) % n;swap(nums[pos], tmp);if(pos == i) break;}}}
};
缺失的第一个正数 【Hard】【置换/原地哈希】

思路:
【方法1】:置换(类似于上一个题目)
- 对
nums[i]<=0||nums[i]>n的元素统一处理。(设置为较大值或数组中出现过的某个1~n的值)。 - 对于
x = nums[i],考虑swap(nums[i], nums[x-1]),即将nums[i]放到他应该在的位置上,如此循环下去,但是注意到当nums[i] == nums[x-1]时会进入死循环。 - 所有
1~n之间的数字都应当被放到对应的位置上,故最后遍历一遍数组,找到第一个不在对应位置之上的元素,便可知答案。
【方法2】:改进开bool型数组,需要空间复杂度O(n),原始数组nums同时充当bool数组(原地哈希)
首先,给出开bool数组的方法,开一个大小为n+5的bool数组flag,flag[i]=true表示i出现,为此只需要找第一个flag[i]==false的i即可。
改进方法如下: - 同方法1。
- 通过第一步
nums数组中应当只有正数。此时,对于一个1~n之间的数字x,我们就将nums[x - 1]中的元素修改为-nums[x - 1](主要不要多次修改,以防负负得正)。即nums数组中元素的正负代表上述bool型数组的true和false,绝对值代表对应元素的值。 - 与方法1类似。
AC代码:
【方法1】:置换
class Solution {
public:int firstMissingPositive(vector<int>& nums){int n = nums.size();for(int i = 0; i < n; ++i) while(nums[i] > 0 && nums[i] <= n && nums[i] != nums[nums[i] - 1]) swap(nums[i], nums[nums[i] - 1]);for(int i = 0; i < n; ++i) if(nums[i] != i + 1) return i + 1;return n + 1;}
};
【方法2】:原地哈希
class Solution {
public:int firstMissingPositive(vector<int>& nums){int n = nums.size();int x;bool flag = false;for(auto x: nums) if(x == 1) flag = true;if(!flag) return 1;for(int i = 0; i < n; ++i) if(nums[i] <= 0 || nums[i] > n) nums[i] = 1;for(int i = 0; i < n; ++i){x = abs(nums[i]) - 1;nums[x] = -abs(nums[x]);}for(int i = 0; i < n; ++i) if(nums[i] > 0) return i + 1;return n + 1;}};
矩阵
矩阵置零【mid】【原地/随机】
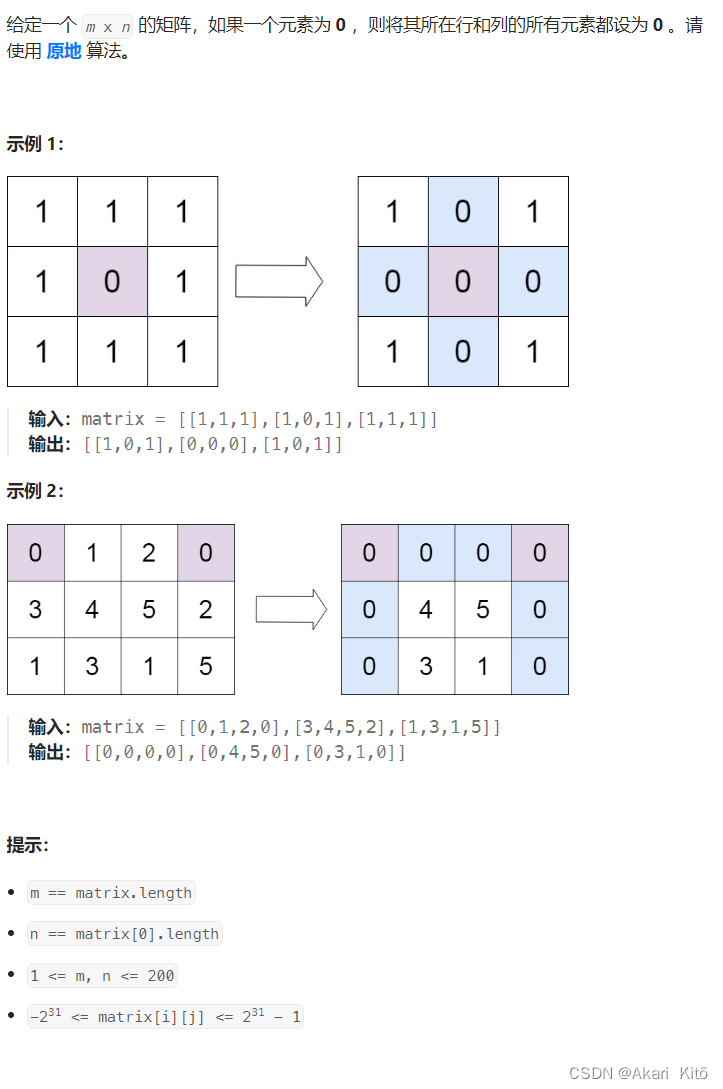
思路:
【方法1】:原地
比较容易想到,开一个长度为n和长度为m的bool型数组,分别表示第i行和第j列是否有0。这样空间复杂度O(n+m)。优化方法是用原数组的第一行和第一列充当这个bool数组。
用两个bool型变量col和row表示第1列,第1行是否有0,之后对于matrix[i][j]==0,将matrix[i][0]和matrix[0][i]标记为0
【方法2】:随机
这个问题的关键是,只会把一开始就有的0所在的行和列全部置为0,后来的出现0不会操作。容易想到的一个思路就是先把有0的行和列中不是0的数字置为一个奇怪的数字(比如inf或是-inf),最后再把这些数改为0,但是发现取值为int的最小值到最大值,所以不行。但是n,m最大为200,随机生成的一个int在矩阵中出现的概率极低,故我们随机生成一个数字作为上述中的奇怪数字即可。(当然是需要判断的,如果运气不好,随机生成的数字正好出现了,就再随机生成一个)
AC代码:
【方法1】:原地
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int n = matrix.size();int m = matrix[0].size();bool col = false, row = false; //column = 列,row = 行for(int i = 0; i < n; ++i){if(!matrix[i][0]){col = true;break;}}for(int i = 0; i < m; ++i){if(!matrix[0][i]){row = true;break;}}for(int i = 1; i < n; ++i){for(int j = 1; j < m; ++j){if(!matrix[i][j]) matrix[i][0] = matrix[0][j] = 0;}}for(int i = 1; i < n; ++i){for(int j = 1; j < m; ++j){if(!matrix[i][0] || !matrix[0][j]) matrix[i][j] = 0; }}if(col) for(int i = 0; i < n; ++i) matrix[i][0] = 0;if(row) for(int i = 0; i < m; ++i) matrix[0][i] = 0;}
};
【方法2】:随机
class Solution {
public:int st_rand(vector<vector<int>>& matrix){int xx = matrix.size();int yy = matrix[0].size();srand(time(NULL));int st;bool flag;while(true){st = rand();flag = false;for(int i = 0; i < xx; ++i){for(int j = 0; j < yy; ++j){if(matrix[i][j] == st) {flag = true;break;}}if(flag) break;}return st;}}void work(vector<vector<int>>& matrix, int x, int y, int st){int xx = matrix.size();int yy = matrix[0].size();for(int i = 0; i < xx; ++i) if(matrix[i][y] != 0) matrix[i][y] = st;for(int i = 0; i < yy; ++i) if(matrix[x][i] != 0) matrix[x][i] = st;}void setZeroes(vector<vector<int>>& matrix) {int xx = matrix.size();int yy = matrix[0].size();int st = st_rand(matrix);for(int i = 0; i < xx; ++i){for(int j = 0; j < yy; ++j){if(matrix[i][j] == 0) work(matrix, i, j, st);}}for(int i = 0; i < xx; ++i){for(int j = 0; j < yy; ++j){if(matrix[i][j] == st) matrix[i][j] = 0;}}}
};