题目描述：

给定两个正整数 a 和 b。

你需要回答 q 个询问。

每个询问给定两个整数 l,r，你需要找到最大的整数 x，满足：

1. x 是 a和 b 的公约数。
2. l≤x≤r。

输入格式

第一行包含两个整数 a,b。

第二行包含一个整数 q。

接下来 q 行，每行包含两个整数 l,r。

输出格式

每个询问输出一行答案，即满足条件的最大的 x�，如果询问无解，则输出 −1−1。

数据范围

前六个测试点满足 1≤a,b≤100，1≤q≤20。
所有测试点满足 1≤a,b≤10^9，1≤q≤10^4，1≤l≤r≤10^9。

输入样例：

9 27
3
1 5
10 11
9 11

输出样例：

3
-1
9

 解题思路:

设d为（a,b）的最大公约数，x为d所有约数，p为质约数；

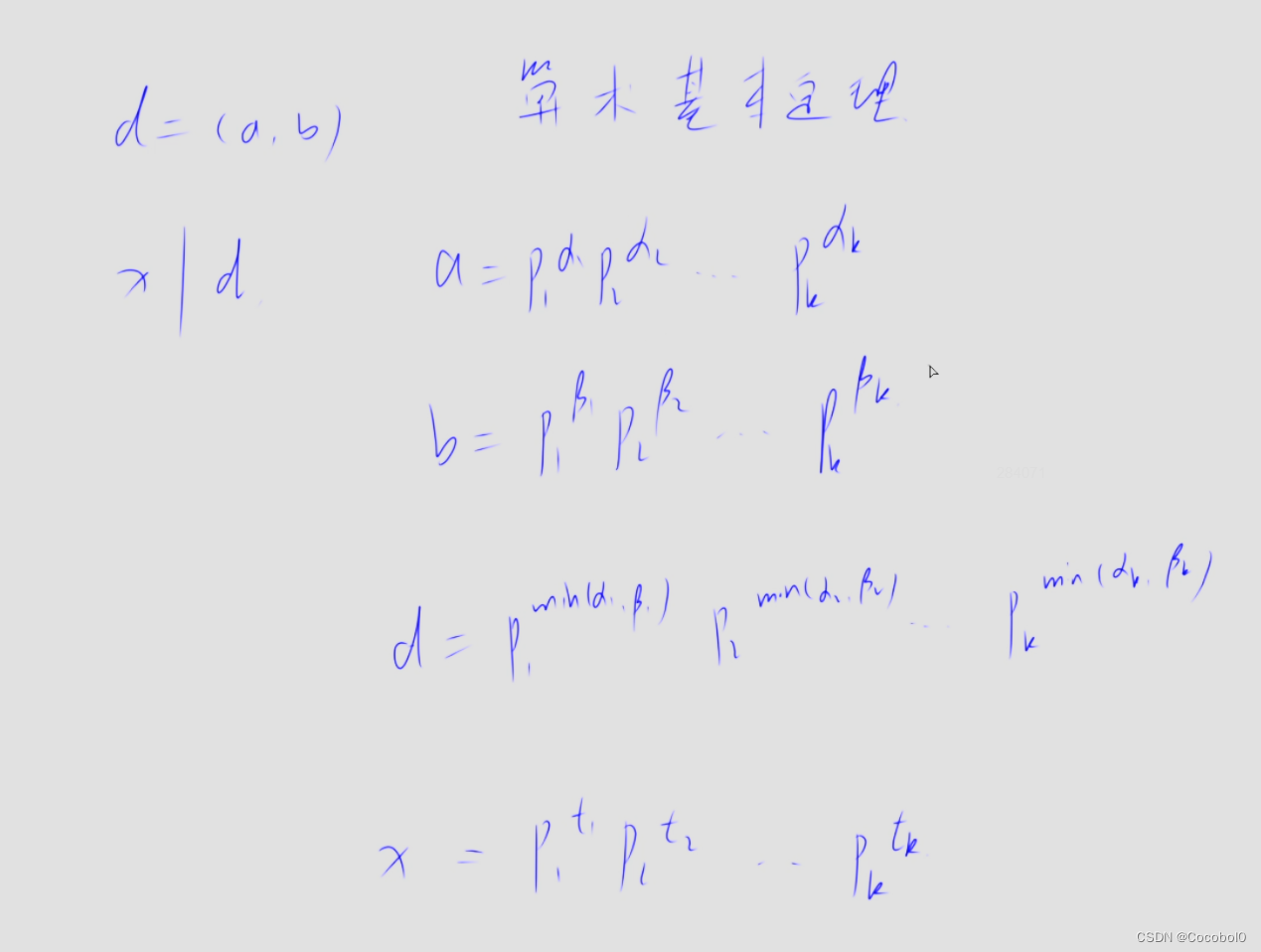
有图可知 a,b质约数和x相同，x为d的约数,因此求出d的所以有约数再排序，找出l-r的最大值即可.

参考代码：

###暴力
```
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
const int N = 1350;
int p[N];
int a,b,cnt;int gcd(int a,int b)
{return b ? gcd(b,a%b) : a;
}void solve(int a,int b)
{int d = gcd(a,b);for(int i=1;i<=d/i;i++){if(d%i==0){p[cnt++] = i;if(i!=d/i) p[cnt++] = d/i;}}sort(p,p+cnt);
}int main()
{scanf("%d%d", &a, &b);solve(a,b);int n;cin>>n;while (n -- ){int l,r;cin>>l>>r;bool st = false;for(int i=cnt-1;i>=0;i--){if(p[i]>=l && p[i]<=r){printf("%d\n",p[i]);st = true;break;}}if(!st) puts("-1");}return 0;
}
```
###二分
```
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;
const int N = 1350;
int p[N];
int a,b,cnt;int gcd(int a,int b)
{return b ? gcd(b,a%b) : a;
}void solve(int a,int b)
{int d = gcd(a,b);for(int i=1;i<=d/i;i++){if(d%i==0){p[cnt++] = i;if(i!=d/i) p[cnt++] = d/i;}}sort(p,p+cnt);
}int main()
{scanf("%d%d", &a, &b);solve(a,b);int n;cin>>n;while (n -- ){int l,r;cin>>l>>r;int L = 0,R = cnt - 1;while(L<R){int mid = L + R + 1 >> 1;if(p[mid]<=r) L = mid;else R = mid - 1;}if(p[L]>=l) printf("%d\n",p[L]);else puts("-1");}return 0;
}
```