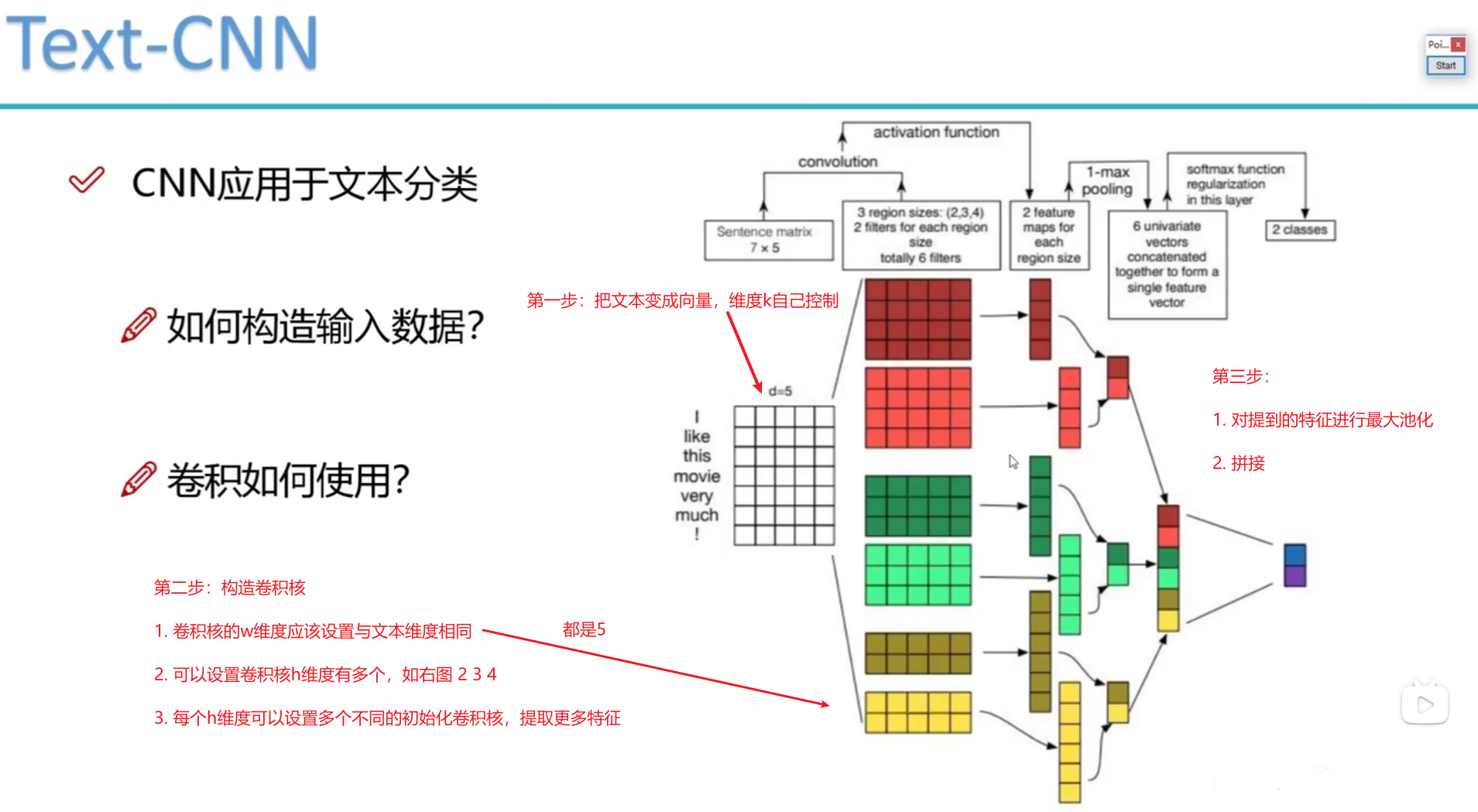
卷积神经网络-批量归一化
- 批量归一化的原理
- 批量归一化的优点
- 批量归一化的应用
- 批量归一化的实现
- TensorFlow实现:
- PyTorch实现:
- 总结
批量归一化(Batch Normalization,简称BN)是一种用于提高深度神经网络训练速度和稳定性的技术。它是由Sergey Ioffe和Christian Szegedy在2015年提出的,并被证明在许多深度神经网络架构中都非常有效。

批量归一化的原理
批量归一化的主要思想是在网络的每一层的激活函数之前,对激活函数的输入进行归一化处理,以使其分布在均值为0、方差为1的范围内,然后再进行平移和缩放,即:


批量归一化的优点
-
加速训练速度:批量归一化可以加速训练过程,允许使用更高的学习率,从而减少训练时间。
-
增强模型稳定性:批量归一化有助于减少梯度消失和梯度爆炸问题,从而提高模型的稳定性。
-
正则化效果:批量归一化具有轻微的正则化效果,有助于减少过拟合。
-
允许更深的网络:由于批量归一化可以缓解梯度问题,因此允许构建更深、更复杂的网络。
批量归一化的应用
批量归一化可以应用于卷积层和全连接层,通常的位置是在激活函数之前。
-
对于全连接层:在全连接层的输出后应用批量归一化,然后再应用激活函数。
-
对于卷积层:在卷积操作后应用批量归一化,然后再应用激活函数。
批量归一化的实现
在深度学习框架(如TensorFlow、PyTorch等)中,批量归一化通常可以很容易地实现。
TensorFlow实现:
import tensorflow as tfmodel = tf.keras.Sequential([tf.keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),tf.keras.layers.BatchNormalization(),tf.keras.layers.MaxPooling2D((2, 2)),tf.keras.layers.Flatten(),tf.keras.layers.Dense(128, activation='relu'),tf.keras.layers.BatchNormalization(),tf.keras.layers.Dense(10, activation='softmax')
])
PyTorch实现:
import torch
import torch.nn as nnclass Model(nn.Module):def __init__(self):super(Model, self).__init__()self.conv1 = nn.Conv2d(1, 32, 3)self.bn1 = nn.BatchNorm2d(32)self.pool = nn.MaxPool2d(2, 2)self.fc1 = nn.Linear(32 * 13 * 13, 128)self.bn2 = nn.BatchNorm1d(128)self.fc2 = nn.Linear(128, 10)def forward(self, x):x = self.pool(F.relu(self.bn1(self.conv1(x))))x = x.view(-1, 32 * 13 * 13)x = F.relu(self.bn2(self.fc1(x)))x = self.fc2(x)return x
总结
批量归一化是一种非常有效的深度学习技术,能够加速模型训练、增强模型稳定性和允许构建更深的网络。在实际应用中,批量归一化已成为许多深度神经网络架构的标准组件。