文章目录
- 1、独立事件的条件概率
- 2、贝叶斯公式、先验概率、后验概率、似然、证据
- 3、马尔可夫链
- 4、正态分布 / 高斯分布
- 5、重参数化技巧
- 6、期望
- 7、KL散度 、高斯分布的KL散度
- 8、极大似然估计
- 9、ELBO :Evidence Lower Bound
- 10、一元二次方程
1、独立事件的条件概率
A 和 B 是两个独立事件:
⇒ \Rightarrow ⇒ P ( A ∣ B ) = P ( A ) P(A|B)=P(A) P(A∣B)=P(A), P ( B ∣ A ) = P ( B ) P(B|A)=P(B) P(B∣A)=P(B),
⇒ \Rightarrow ⇒ P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) P(A,B|C)=P(A|C)P(B|C) P(A,B∣C)=P(A∣C)P(B∣C)
2、贝叶斯公式、先验概率、后验概率、似然、证据
贝叶斯公式:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
- 先验概率(prior):P(A)
- 后验概率(posterior):P(A|B)
- 似然 (likelihood):P(B|A)
- 证据(evidence):P(B)
举例:

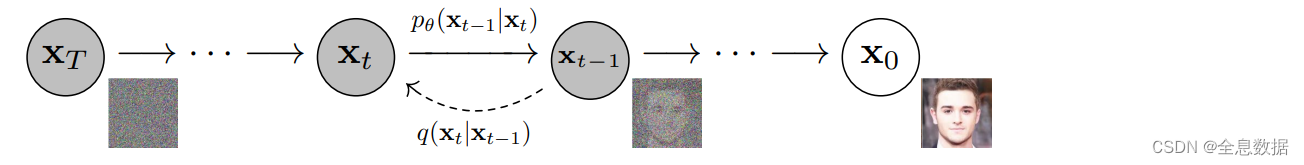
P ( x t − 1 ∣ x t ) = P ( x t ∣ x t − 1 ) P ( x t − 1 ) P ( x t ) P(x_{t-1}|x_t)=\frac{P(x_t|x_{t-1})P(x_{t-1})}{P(x_t)} P(xt−1∣xt)=P(xt)P(xt∣xt−1)P(xt−1)
3、马尔可夫链
马尔可夫链:下一状态的概率分布仅取决于当前状态,与过去的状态无关
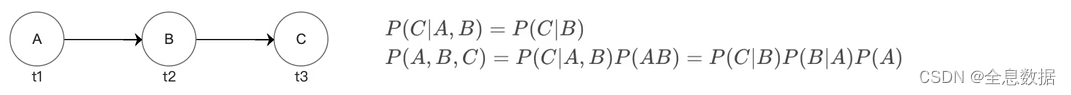
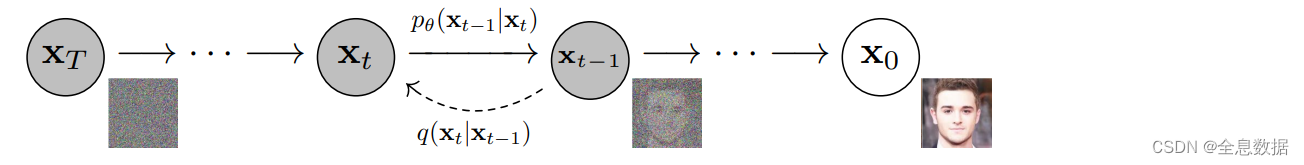
P ( x t ∣ x t − 1 , x t − 2 . . . x 1 x 0 ) = P ( x t ∣ x t − 1 ) P(x_t|x_{t-1},x_{t-2}...x_1x_0)=P(x_t|x_{t-1}) P(xt∣xt−1,xt−2...x1x0)=P(xt∣xt−1)
正向扩散过程: q ( x 0 : x T ) = q ( x 0 ) q ( x 1 ∣ x 0 ) q ( x 2 ∣ x 1 ) . . . q ( x T − 1 ∣ x T − 2 ) q ( x T ∣ x T − 1 ) q(x_0:x_T)=q(x_0)q(x_1|x_0)q(x_2|x_1)...q(x_{T-1}|x_{T-2})q(x_T|x_{T-1}) q(x0:xT)=q(x0)q(x1∣x0)q(x2∣x1)...q(xT−1∣xT−2)q(xT∣xT−1)
逆向扩散过程: p ( x 0 : x T ) = p ( x T ) p ( x T − 1 ∣ x T ) p ( x T − 2 ∣ x T − 1 ) . . . p ( x 1 ∣ x 2 ) p ( x 0 ∣ x 1 ) p(x_0:x_T)=p(x_T)p(x_{T-1}|x_T)p(x_{T-2}|x_{T-1})...p(x_1|x_2)p(x_0|x_1) p(x0:xT)=p(xT)p(xT−1∣xT)p(xT−2∣xT−1)...p(x1∣x2)p(x0∣x1)
4、正态分布 / 高斯分布
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e−2σ2(x−μ)2
x ∼ N ( μ , σ 2 ) x\sim \mathcal{N}(\mu,\sigma^2) x∼N(μ,σ2)
高斯分布的性质:
A、如果 X ∼ N ( μ , σ 2 ) X\sim \mathcal{N}(\mu,\sigma^2) X∼N(μ,σ2),那么 a X + B ∼ N ( a μ + b , a 2 σ 2 ) aX+B\sim \mathcal{N}(a\mu+b,a^2\sigma^2) aX+B∼N(aμ+b,a2σ2)
B、两个正态分布相加,其结果也是正态分布:
X ∼ N ( μ 1 , σ 1 2 ) X\sim \mathcal{N}(\mu_1,\sigma_1^2) X∼N(μ1,σ12); Y ∼ N ( μ 2 , σ 2 2 ) Y\sim \mathcal{N}(\mu_2,\sigma_2^2) Y∼N(μ2,σ22),则 X + Y ∼ N ( μ 1 + μ 2 , σ 1 2 + σ 2 2 ) X+Y\sim\mathcal{N}(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2) X+Y∼N(μ1+μ2,σ12+σ22)
5、重参数化技巧
对于高斯分布: X ∼ N ( μ , σ 2 ) X\sim \mathcal{N}(\mu,\sigma^2) X∼N(μ,σ2),采样这个操作本身是不可导的,也就无法通过BP来对参数进行优化。但是我们可以通过重参数化技巧,将简单分布的采样结果变换到特定分布中,如此一来则可以对参数进行求导,
具体操作:
A、引入服从标准正态分布的随机变量: z ∼ N ( 0 , 1 ) z\sim\mathcal{N}(0,1) z∼N(0,1)
B、令 x = μ + σ z x=\mu+\sigma z x=μ+σz,这样就满足 X ∼ N ( μ , σ 2 ) X\sim\mathcal{N}(\mu,\sigma^2) X∼N(μ,σ2)
6、期望
期望是指随机变量取值的平均值,用来刻画随机变量的集中位置,
(1)离散型随机变量
离散型随机变量X的取值为 x 1 , x 2 , x 3 , . . . . . . . , x n x_1,x_2,x_3,.......,x_n x1,x2,x3,.......,xn,对应的概率为 p 1 , p 2 , p 3 , . . . . . . , p n p_1,p_2,p_3,......,p_n p1,p2,p3,......,pn,
则X的期望为: E ( X ) = ∑ i = 1 n x i p i E(X)=\sum_{i=1}^{n}x_ip_i E(X)=∑i=1nxipi
------------------------------------------------------------------------------------------------
若离散变量 Y Y Y符合函数 Y = g ( X ) Y= g(X) Y=g(X), g ( X ) g(X) g(X)是连续函数,且 ∑ i = 1 n g ( x i ) p i \sum_{i=1}^n g(x_i)p_i ∑i=1ng(xi)pi绝对收敛,
则离散变量 Y Y Y的期望为: E ( X ) = ∑ i = 1 n g ( x i ) p i E(X)=\sum_{i=1}^n g(x_i)p_i E(X)=∑i=1ng(xi)pi
(2)连续型随机变量
连续型随机变量 X X X的概率密度函数为 f ( x ) f(x) f(x),
则 X X X的期望为: E ( X ) = ∫ − ∞ ∞ x f ( x ) d x E(X)=\int_{-\infty}^\infty xf(x){\rm d}x E(X)=∫−∞∞xf(x)dx,
若随机变量 Y Y Y符合函数 Y = g ( x ) Y = g(x) Y=g(x),且 ∫ − ∞ ∞ g ( x ) f ( x ) d x \int_{-\infty}^\infty g(x)f(x){\rm d}x ∫−∞∞g(x)f(x)dx绝对收敛,
则随机变量 Y Y Y的期望为: E ( Y ) = ∫ − ∞ ∞ g ( x ) f ( x ) d x E(Y)=\int_{-\infty}^\infty g(x)f(x){\rm d}x E(Y)=∫−∞∞g(x)f(x)dx
注意: 对于连续型随机变量,期望就是积分,满足条件的积分也可以写成期望的形式。这在之后的 公式推导过程中,我们会使用到期望与积分写法的转换,
7、KL散度 、高斯分布的KL散度
KL散度的作用: 用于衡量2个概率分布(分布 p p p和分布 q q q)之间的差异,
D K L ( p ∣ ∣ q ) = H ( p , q ) − H ( p ) = ∫ x p ( x ) l o g p ( x ) q ( x ) d x = E x ∼ p ( x ) [ l o g p ( x ) q ( x ) ] D_{KL}(p||q)=H(p,q)-H(p)=\int_x p(x)log\frac{p(x)}{q(x)}dx=E_{x\sim p(x)}[log\frac{p(x)}{q(x)}] DKL(p∣∣q)=H(p,q)−H(p)=∫xp(x)logq(x)p(x)dx=Ex∼p(x)[logq(x)p(x)]
其中:
H ( p , q ) H(p, q) H(p,q)表示分布 p p p和分布 q q q的交叉熵, H ( p ) H(p) H(p)表示分布 p p p的熵,
KL散度的重要性质:
- D K L ( p ∣ ∣ q ) ≥ 0 D_{KL}(p||q)\ge0 DKL(p∣∣q)≥0
- 当分布 p p p与分布 q q q完全一样时, D K L ( p ∣ ∣ q ) = 0 D_{KL}(p||q)=0 DKL(p∣∣q)=0
- 对于相同的分布 p p p和分布 q q q,这里所说的相同的分布是 D K L ( p ∣ ∣ q ) D_{KL}(p||q) DKL(p∣∣q)与 D K L ( q ∣ ∣ p ) D_{KL}(q||p) DKL(q∣∣p)中的2个 p p p和2个 q q q是一样的, D K L ( p ∣ ∣ q ) D_{KL}(p||q) DKL(p∣∣q)与 D K L ( q ∣ ∣ p ) D_{KL}(q||p) DKL(q∣∣p)计算所得到的值不一样,
对于 D K L ( p ∣ ∣ q ) D_{KL}(p||q) DKL(p∣∣q),我们一般认为 p ( x ) p(x) p(x)是真实分布, q ( x ) q(x) q(x)是预测分布, D K L ( p ∣ ∣ q ) D_{KL}(p||q) DKL(p∣∣q)是
求预测分布 q ( x ) q(x) q(x)与真实分布 p ( x ) p(x) p(x)之间的差距,
高斯分布的KL散度:
p ( x ) = N ( μ 1 , σ 1 ) = 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 p(x)=\mathcal{N}(\mu_1,\sigma_1)=\frac{1}{\sqrt{2\pi}\sigma_1}e^-\frac{(x-\mu_1)^2}{2\sigma_1^2} p(x)=N(μ1,σ1)=2πσ11e−2σ12(x−μ1)2,
q ( x ) = N ( μ 2 , σ 2 ) = 1 2 π σ 2 e − ( x − μ 2 ) 2 2 σ 1 2 q(x)=\mathcal{N}(\mu_2,\sigma_2)=\frac{1}{\sqrt{2\pi}\sigma_2}e^-\frac{(x-\mu_2)^2}{2\sigma_1^2} q(x)=N(μ2,σ2)=2πσ21e−2σ12(x−μ2)2,
K L ( N ( x ∣ μ 1 , ∑ 1 ) ∣ ∣ N ( x ∣ μ 2 , ∑ 2 ) ) = 1 2 [ l o g ∑ 2 ∑ 1 − K + t r ( ∑ 2 − 1 ∑ 1 ) + ( μ 1 − μ 2 ) T ∑ 2 − 1 ( μ 1 − μ 2 ) ] {\rm KL}(\mathcal{N}({\rm x}|\mu_1,\sum_1)||\mathcal{N}({\rm x}|\mu_2,\sum_2))=\frac{1}{2}\big[ log\frac{\sum_2}{\sum_1}-K+tr(\sum_2^{-1}\sum_1)+(\mu_1-\mu_2)^T\sum_2^{-1}(\mu_1-\mu_2)\big] KL(N(x∣μ1,∑1)∣∣N(x∣μ2,∑2))=21[log∑1∑2−K+tr(∑2−1∑1)+(μ1−μ2)T∑2−1(μ1−μ2)],
D K L ( p , q ) = l o g σ 2 σ 1 − 1 2 + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 D_{KL}(p,q)=log\frac{\sigma_2}{\sigma_1}-\frac{1}{2}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} DKL(p,q)=logσ1σ2−21+2σ22σ12+(μ1−μ2)2,
推导过程: https://blog.csdn.net/hegsns/article/details/104857277
8、极大似然估计
概括描述:已知抽取的样本,求概率分布的参数
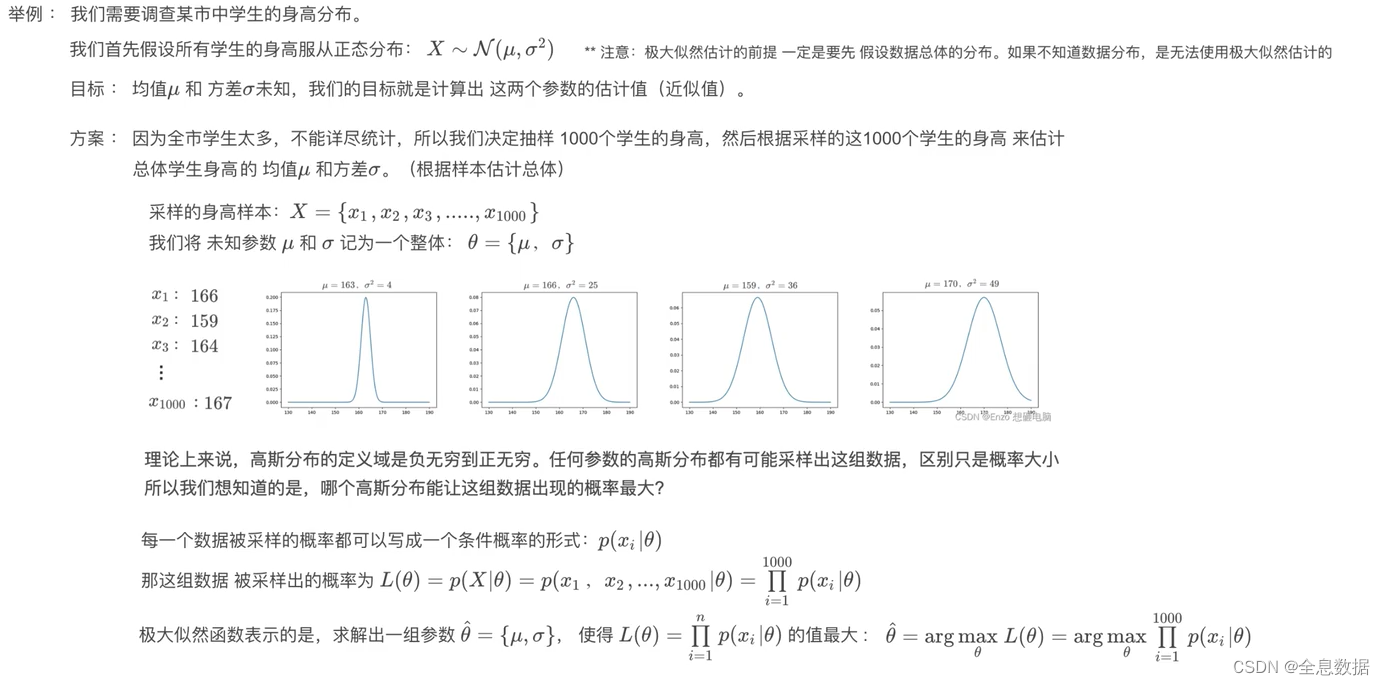
-----------------------------------------------------------------------------------------------------------------------------

9、ELBO :Evidence Lower Bound

10、一元二次方程