本篇主要介绍马尔科夫决策(MDP)过程,在介绍MDP之前,还需要对MP,MRP过程进行分析。
什么是马尔科夫,说白了就是带遗忘性质,下一个状态S_t+1仅与当前状态有关,而与之前的状态无关。

为什么需要马尔科夫性——简化环境模型。帮助强化学习来学习。
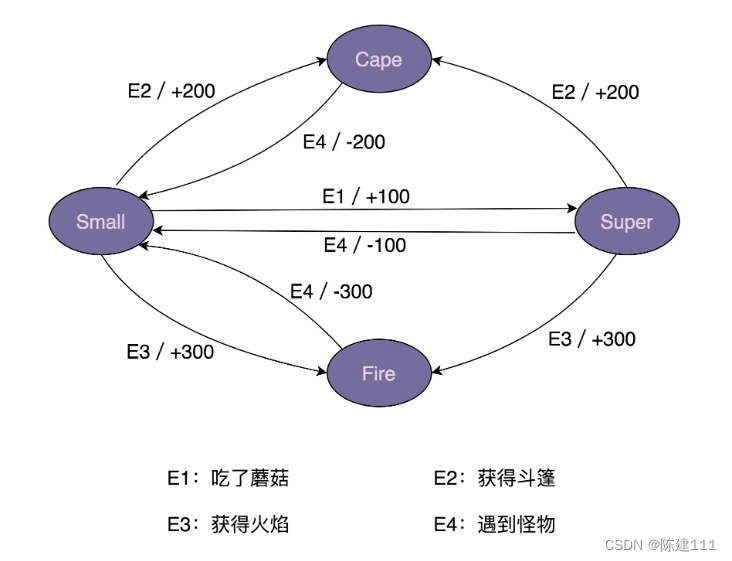
马尔科夫过程:通过状态转移概率的实现的过程,马尔科夫过程是一个**<S,P>,S是有限状态集合,P是状态转移概率,状态转移概率矩阵为P_ij
马尔科夫奖励过程:在马尔可夫过程的基础上增加奖励函数R和衰减系数γ,基本上一谈到奖励就会有折扣因子的存在。表示为 (S,P,R,γ)。
R是一个奖励函数,S状态下的奖励是某一时t处在状态s下在下一个时刻(t+1)能获得的期望奖励。
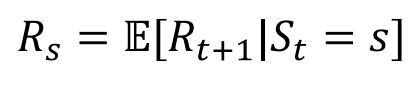
期望的含义也就是说与概率是相关的,求概率平均。
累计回报:从t时刻所得到的折扣回报总和。折扣因子表示了对未来奖励的重视程度。越小就是越短视,越大就越远视。
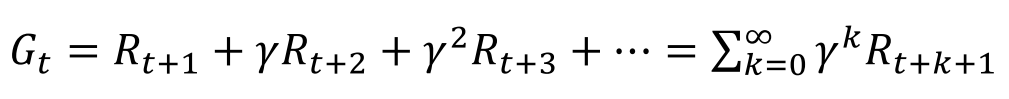
价值函数:价值函数给出了某一状态或某一行为的长期价值。
状态价值函数和动作价值函数来看待问题(强化学习最重要的公式)

注意这里的价值函数可能是状态价值,也可以是动作价值**
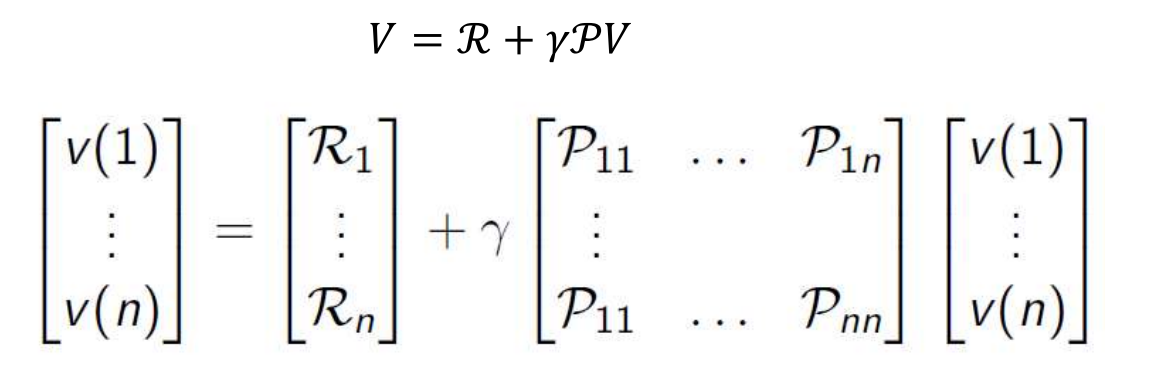
马尔科夫一个重要的内容就是要通过bellman方程求解状态价值函数。
如何求解?
n比较小时直接计算,n比较大时通过迭代来求解:
- 动态规划
- 蒙特卡洛评估
- 时序差分学习
最后就是马尔科夫决策过程MDP了,由(SAPRγ)五元组成。
状态动作,状态转移概率,回报函数,折扣因子
与马尔科夫过程不同的是状态转移多了一个动作的选项。
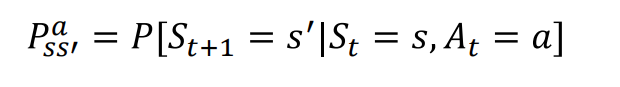
MDP就引入了policy的概念,策略是决定行为的机制。强化学习的本质就是最优策略的寻找。
策略同样是仅与当前状态有关。可以是随机策略或者确定性策略。
两大价值函数的引入:


最优理论就是关于价值函数的:
从所有策略产生的状态价值函数中,选取使状态s价值最大的函数:
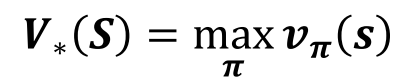
从所有策略产生的行为价值函数中,选取是状态行为对 价值最大的函数:
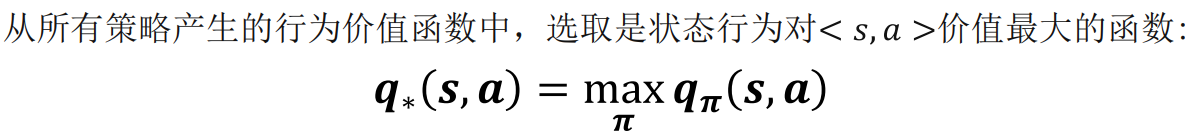
后面我回再推导一下这些函数关系式,并且比较相似的内容进行学习。
后续内容:
线性mpc
包括等式约束和不等式约束
非线性mpc
构建优化问题
泰勒展开线性化
KKT条件处理不等式约束
求解SQP问题
一些重要参数
预测窗口
终端项
预见性的控制(优化问题与控制效果)
SQP解决MPC的优化问题。(解一个序列控制量问题)
另一种求解思路:
HJB方程。
成本函数-状态方程——哈密顿函数
转为泛函优化问题:
变分法,分部积分,求极点的思路。
构造哈密尔顿函数
状态方程,协状态方程
控制最优条件 终值和初值条件
线性模型+二次型优化问题。
求解黎卡提方程。