本文为 Data Shapley: Equitable Valuation of Data for Machine Learning 的阅读笔记，涉及论文中的 Data Shapley Value 计算公式、两种实现算法、实验应用部分的梳理。
为理解 Data Shapley Value，本文首先讨论 Shapley Value的相关内容，利用一个具体实例计算 Shapley Value 并讨论其计算公式。而后，解释一脉相承的 Data Shapley Value 计算公式、两种实现算法的伪代码。
欢迎讨论！若有错误，敬请指正！

---

Shapley Value

Shapley value 的核心思想：在一个合作游戏中，每个玩家的价值可以通过其对所有可能的合作联盟（玩家子集）的贡献平均值来衡量。

Shapley value 的引例 – “哪位程序员的贡献最大”

某公司有三个程序猿，分别是屌丝 A，大佬 B，美女 C。如果大家不合作，A 每个季度可以完成 3 个项目，B 每个季度可以完成 10 个项目，C 每个季度只能完成 1 个项目。但是老板小王为了充分挖掘员工潜力，合理配置公司资源，让 A，B，C 尝试了各种合作模式。

王老板观察发现，屌丝都是潜力股，美女都是催化剂：屌丝 A 和大佬 B 合作每个季度可以完成 15 个项目，合作效果提升还行；屌丝 A 和美女 C 合作每个季度可以完成 50 个项目，合作效果爆炸；大佬 B 和美女 C 合作每个季度仅完成了 12 个项目，看来对大佬来说不影响拔刀的速度就不错了；ABC 一起合作每个季度可以完成 70 个项目。最终王老板拍板让 ABC 以后就一起工作，按照小组完成的项目数额外发放项目奖金。那么，如何根据员工的贡献值来确定哪位员工的奖金最多？

说 A 的同学：明显屌丝是潜力股，虽然单独工作表现一般，但是和美女一起合作，大大激发了工作热情，肯定是 A 贡献最多！说 B 的同学：应该是大佬贡献最大，因为单独来看，大佬本身能力是最强的！说 C 的同学：应该是美女贡献最大，虽然美女单独工作没什么效率，但显然对团队的影响无法替代！

为解决这一问题，我们采用 shapley 值尝试求解这一问题。设想我们以某种顺序将 ABC 放到合作队伍中（合作队伍一开始为空），那么合作的组合会有 3!=6 种，每种组合的概率均为 1/6，各种组合及各员工的贡献如下表所示：

集合序号	加入顺序	A加入的贡献	B加入的贡献	C加入的贡献	概率
1	A+B+C	3-0=3	15-3=12	70-15=55	1/6
2	A+C+B	3-0=3	70-50=20	50-3=47	1/6
3	B+A+C	15-10=5	10-0=10	70-15=55	1/6
4	B+C+A	70-12=58	10-0=10	12-10=2	1/6
5	C+A+B	50-1=49	70-50=20	1-0=1	1/6
6	C+B+A	70-12=58	12-1=11	1-0=1	1/6

在 A+B+C 的组合中，A 的贡献为 A 单独工作的效率 3；B 的贡献为 A+B 一起工作的效率与 A 单独工作效率的差值：15-3=12；C 的贡献为 A+B+C 一起工作的效率与 A+B 一起工作的效率的差值：70-15=55。

通过计算数学期望来计算各员工的贡献，得 A 的期望贡献：(3+3+5+58+49+58)/6=176/6；B 的期望贡献：(12+20+10+10+20+11)/6=83/6；C 的期望贡献： (55+47+55+2+1+1)/6=161/6。所有员工的期望贡献和为：(176+83+161)/6=70，刚好是 ABC 的整体合作效果，验证了我们计算的合理性。

对贡献值归一后可知，A 的贡献占比是 29.33%，B 的贡献占比是 13.83%，C 的贡献占比是 26.83%。所以，A 的贡献是最多的，C 也次之，B 最少。

Shapley value 概念

假设有 $n$ 位合作人，记 $D=1,2,...,n$，$S$ 为 $D$ 中不含第 $i$ 位合作者的集合，即 S ⊆ D − { i } S \subseteq D-\{i\} S⊆D−{i}，$V(S)$ 表示集合 $S$ 中的贡献值。

边际贡献

第 $i$ 位合作人的贡献，一般采用集合 $S$ 与第 $i$ 位合作人合作后的贡献减去集合 $S$ 的贡献来描述。即，$V(i)=V(S\cup i)-V(S)$。

合作者加入团队的顺序/合作者在团队中的排序会影响边际贡献值，例如引例中，集合序号 3、4 中 A 的贡献值。

边际贡献对应的概率

每个集合出现具有一定的概率，下面以 $i=1$​ 为例，绘制权重分配树，分析每种集合出现的概率。当 $i=1$ 时，$|S|$ 集合人数存在 $n-1$ 种情况，每种情况出现的概率为 $1/n$。其中，若 $|S|=1$ 时，$|S|$ 集合又可以细分为 $C_{n-1}^{|1|}$ 种情况，分别是：$1,2,1,3,...1,n$，每种情况出现的概率为 $\frac{1}{C_{n-1}^{|S|}}$。由归纳法知，当 $i=1$ 时，每种集合存在的概率可以用通式表示为：$\frac{1}{n}\times \frac{1}{C_{n-1}^{|S|}}$​，整理后为：$\begin{array}{rl}\frac{1}{n}\times \frac{1}{C_{n-1}^{|S|}}& =\frac{1}{n}\times \frac{(n-1-|S|)!(|S|)!}{(n-1)!}=\frac{(n-|S|-1)!(|S|)!}{n!}\end{array}$​。

不难发现，概率值仅与 $|S|$ 大小有关，与集合 $S$​ 中的排序无关。

关于概率值 $\frac{(n-|S|-1)!(|S|)!}{n!}$ 的理解：$(n-|S|-1)!$ 表示 $i$ 后元素的排列组合数，$(|S|)!$ 表示 $i$ 前元素的排列数，$n!$ 表示所有元素的排列数。模型解释–Shapley Values - 简书 (jianshu.com)

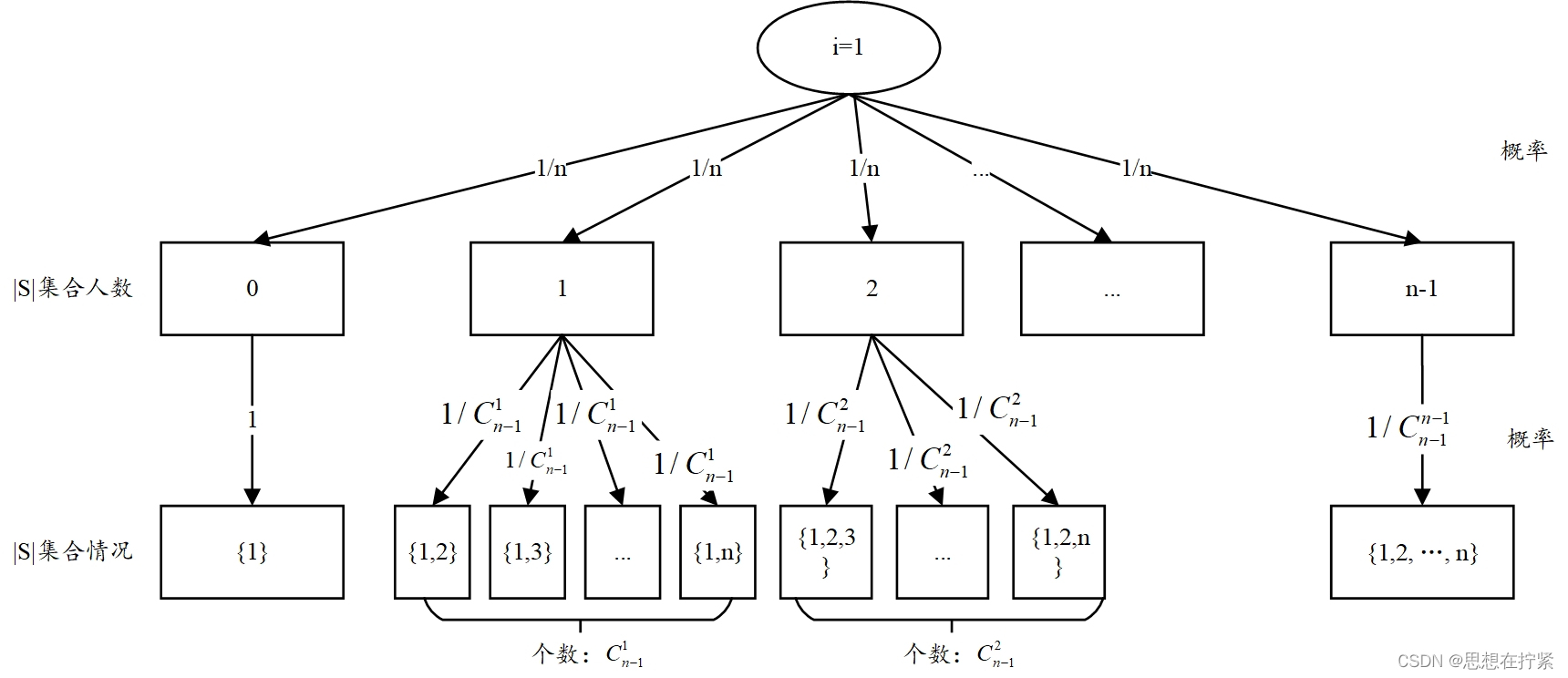
存在三种理解概率值的角度：构造联盟角度-总体平等性、联盟内外平等性角度-平均加权、联盟中参与人贡献平等性的角度-平等贡献性。见 Shapley_Value公式推导

公式理解

由以上分析，可表示出第 $i$ 合作者的期望贡献 ${\varphi }_i$ 为：
ϕ i = ∑ S ⊆ D − { i } ( n − ∣ S ∣ − 1 ) ! ( ∣ S ∣ ) ! n ! [ V ( S ∪ { i } ) − V ( S ) ] \phi_i=\sum_{S \subseteq D-\{i\}} \frac{(n-|S|-1) !(|S|)!}{n!}[V(S \cup\{i\})-V(S)] ϕi​=S⊆D−{i}∑​n!(n−∣S∣−1)!(∣S∣)!​[V(S∪{i})−V(S)]
在引例中，计算 Shapley value 过程中详细列出所有情况，过于复杂。现可以直接以上述公式求得每个程序员的贡献度。

以程序员 A 为例，计算其 Shapley value - ${\varphi }_A$：
ϕ A = ∑ S ⊆ D − { i } ( n − ∣ S ∣ − 1 ) ! ( ∣ S ∣ ) ! n ! [ V ( S ∪ { i } ) − V ( S ) ] = ∑ S ⊆ { A , B , C } − { A } ( 3 − ∣ S ∣ − 1 ) ! ( ∣ S ∣ ) ! 3 ! [ V ( S ∪ { A } ) − V ( S ) ] = ( 3 − 0 − 1 ) ! ( 0 ) ! 3 ! [ V ( { A } ) − V ( ∅ ) ] + ( 3 − 1 − 1 ) ! ( 1 ) ! 3 ! [ V ( { B } ∪ { A } ) − V ( B ) ] + ( 3 − 1 − 1 ) ! ( 1 ) ! 3 ! [ V ( { C } ∪ { A } ) − V ( C ) ] + ( 3 − 2 − 1 ) ! ( 2 ) ! 3 ! [ V ( { B C } ∪ { A } ) − V ( B C ) ] = 2 ! 3 ! ∗ 3 + 1 3 ! ∗ [ 15 − 10 ] + 1 3 ! ∗ [ 50 − 1 ] + 2 ! 3 ! ∗ [ 70 − 12 ] = 1 + 5 6 + 49 6 + 58 3 = 176 6 \begin{align*} \phi_A &=\sum_{S \subseteq D-\{i\}} \frac{(n-|S|-1) !(|S|)!}{n!}[V(S \cup\{i\})-V(S)] \\ &=\sum_{S \subseteq\{A, B, C\}-\{A\}} \frac{(3-|S|-1) !(|S|) !}{3 !}[V(S \cup\{A\})-V(S)] \\ &=\frac{(3-0-1) !(0) !}{3 !}[V(\{A\})-V(\varnothing)]+\frac{(3-1-1) !(1) !}{3 !}[V(\{B\} \cup\{A\})-V(B)]+\frac{(3-1-1) !(1) !}{3 !}[V(\{C\} \cup\{A\})-V(C)]+\frac{(3-2-1) !(2) !}{3 !}[V(\{B C\} \cup\{A\})-V(B C)] \\ &=\frac{2 !}{3 !} * 3+\frac{1}{3 !} *[15-10]+\frac{1}{3 !} *[50-1]+\frac{2 !}{3 !} *[70-12]=1+\frac{5}{6}+\frac{49}{6}+\frac{58}{3}=\frac{176}{6} \end{align*} ϕA​​=S⊆D−{i}∑​n!(n−∣S∣−1)!(∣S∣)!​[V(S∪{i})−V(S)]=S⊆{A,B,C}−{A}∑​3!(3−∣S∣−1)!(∣S∣)!​[V(S∪{A})−V(S)]=3!(3−0−1)!(0)!​[V({A})−V(∅)]+3!(3−1−1)!(1)!​[V({B}∪{A})−V(B)]+3!(3−1−1)!(1)!​[V({C}∪{A})−V(C)]+3!(3−2−1)!(2)!​[V({BC}∪{A})−V(BC)]=3!2!​∗3+3!1​∗[15−10]+3!1​∗[50−1]+3!2!​∗[70−12]=1+65​+649​+358​=6176​​

Shapley value 存在负值，表示负贡献。

Shapley value 的性质/公理

以下三条性质/公理，能将 ${\varphi }_i$ 确定为比例常数。

对称性

每个参与人的贡献/获得的价值与它在集合 D = { 1 , 2 , … , n } D=\{1,2,…,n\} D={1,2,…,n} 中的排列位置无关。数学描述： S ⊆ D − { i , j } , V ( S ∪ i ) = V ( S ∪ j ) , 则 ϕ i = ϕ j S \subseteq D-\{i,j\},V(S\cup i)=V(S\cup j),则 \phi_i=\phi_j S⊆D−{i,j},V(S∪i)=V(S∪j),则ϕi​=ϕj​。

有效性

1. 如果一个参与者在所有可能的联盟中都没有对结果的影响力，那么该参与者的 Shapley value 应为零。数学描述： S ⊆ D − { i } , V ( S ) = V ( S ∪ i ) , 则 ϕ i = 0 S \subseteq D-\{i\},V(S)=V(S \cup i),则 \phi_i=0 S⊆D−{i},V(S)=V(S∪i),则ϕi​=0
2. 所有参与者的 Shapley value 之和等于合作博弈的总价值。数学描述：$\sum {\varphi }_i=a$，$a$ 为合作博弈的总价值。

可加性

n 个人同时进行两项互不影响的合作，则两项合作的分配也应互不影响，每人的分配额是两项合作单独进行时应分配数的和。数学描述：当 $V=V_1+V_2$ 时，有 $\varphi ={\varphi }_i+{\varphi }_j$。一般来说，记 $V_k=-L_k$，$L_k$ 表示损失值，为正数，损失值越大，$V_k$ 越小。

Shapley value 的评价

Shapley 值方法很公平，在经济、金融、管理、政治中都有不少的推广应用。比如多方金融投资合作如何分配利润；不同人数的党派团体如何更科学地设置投票通过票数；安全管理团队中按照重要性对事故中的不同责任方进行责任判定等等。在机器学习中，也可以使用 Shapley 值方法对不同的特征进行重要性评价，进行特征的筛选工作，即使是深度神经网络这种黑盒模型也可以获悉不同特征对于整个算法的贡献分布。

缺点：对于 n 值很大的情况，计算很不友好。对于 $n$ 个数据点，可能的排列数量是 $n!$。对于 $n$ 个数据点，有 $2^n$ 个子集（包括空集和整个数据集）。因为每个数据点都有两种可能：要么在子集中，要么不在。对于 $n$ 个数据点，第一个数据点可以选择在或不在一个子集，第二个数据点同样有这两种选择，以此类推，直到最后一个数据点。不包含 $i$ 的子集有 $2^{n-1}$ 个（包括空集）。有几种补救办法，有的是将合伙人分成若干组，按照组为最小合作单位进行计算；有的则是只考虑 n−1 大小的组合上增加合伙人带来的边际贡献等。无论是何种方法，本质上都和本文核心内容类似。

1. 满足公平数据估值的几个自然属性（natural properties）
2. 在提供洞察哪些数据对给定的学习任务更有价值方面，它比流行的“留一分”或杠杆得分更强大
3. 低 Shapley 值的数据有效捕获异常值和腐败
4. 高 Shapley 值的数据能告知需要获取何种类型的新数据来改进预测器

以上四点，论文中的 Experiments & Applications有涉及。关于这部分的梳理可见：回答十问Q6 Data Shapley: Equitable Valuation of Data for Machine Learning (readpaper.com)

Data Shapley Value

Data Shapley Value 依赖于数据集、算法、性能度量指标。

训练数据 D = { x i ， y i } 1 n D=\{x_i，y_i\}_1^n D={xi​，yi​}1n​ 是一个固定大小的 n 个数据点的集合，无分布和独立性假设。其中，$x_i$ 是特征，$y_i$ 是标签。$S$ 为数据集 $D$ 的子集。关于符号 $S$、$D$，除了表示数据，也能表示数据对应的索引

$\mathcal{A}$ 是用数据集生成预测器（predictor, $f$）的算法。

$V$ 是性能度量指标，量化每个数据对预测器 $f$ 的作用。$V(S,\mathcal{A})$ 或 $V(S)$ 表示在数据集 $S$ 上训练的预测器的性能。一般采用留一法（Leave-one-out, LOO），即比较在整个数据集上训练的预测器性能相较于减去一点数据后的数据集上训练的预测器性能的减少量。本文采用 Shapley 而不用留一法的原因：LOO 只考虑单个数据点的移除对模型性能的影响，不考虑各数据点间的关系；不满足公平性、对称性、可加性等性质；计算效率低下。

第 $i$ 个数据点（i-th datum）的 data shapely value 记为：${\varphi }_i(D,\mathcal{A},V)={\varphi }_i(V)={\varphi }_i\in R$

ϕ i = C ∑ S ⊆ D − { i } V ( S ∪ { i } ) − V ( S ) ( n − 1 ∣ S ∣ ) \phi_i=C \sum_{S \subseteq D-\{i\}} \frac{V(S \cup\{i\})-V(S)}{\left(\begin{array}{c}n-1 \\ |S|\end{array}\right)} ϕi​=CS⊆D−{i}∑​(n−1∣S∣​)V(S∪{i})−V(S)​

其中，$S$ 为 $D$ 中随机一个不含有 $i$ 的子集，$\left(\begin{array}{c}n-1\\ |S|\end{array}\right)$ 是组合数的一种写法，也可写为 $C_{n-1}^{|S|}$。求和符号表示讨论 $D$ 中所有不含数据点 $i$ 的子集 $S$。上式和 Shapley 计算公式唯一区别在于：上式中设了任意常数 $C$，而 Shapley 公式中为确定的 $1/n$。

实现方法

截断蒙特卡洛 Shapley 算法（Truncated Monte Carlo Shapley, TMC-Shapley）

此算法是针对整个数据集进行分析的，不需要选取子集 $S$。每次迭代都会对整个数据集中的所有数据点进行一次重新排列，一般对于 $n$ 个数据点，可能的排列数量是 $n!$​​。算法会随机选择所有数据点排列情况中的一部分，计算各数据点的Shapley 值的近似结果。

需要注意的是，此算法的准确性和效率依赖于迭代次数和数据集的大小，因此在实际应用中需要根据具体情况调整参数。

求解步骤

Input: Train data D = { 1 , … , n } D=\{1, \ldots, n\} D={1,…,n}, learning algorithm
$\mathcal{A}$, performance score $V$
Output: Shapley value of training points: ${\varphi }_1,\dots ,{\varphi }_n$
Initialize ${\varphi }_i=0$ for $i=1,\dots ,n$ and $t=0$
while Convergence criteria not met do
$t\leftarrow t+1$
${\pi }^t$ : Random permutation of train data points
$v_0^t\leftarrow V(\varnothing ,\mathcal{A})$
for j ∈ { 1 , … , n } j \in\{1, \ldots, n\} j∈{1,…,n} do
if $\left|V(D)-v_{j-1}^t\right|<$ Performance Tolerance then
$v_j^t=v_{j-1}^t$
else
v j t ← V ( { π t [ 1 ] , … , π t [ j ] } , A ) v_j^t \leftarrow V\left(\left\{\pi^t[1], \ldots, \pi^t[j]\right\}, \mathcal{A}\right) vjt​←V({πt[1],…,πt[j]},A)
end if
${\varphi }_{{\pi }^t[j]}\leftarrow \frac{t-1}{t}{\varphi }_{{\pi }^{t-1}[j]}+\frac{1}{t}\left(v_j^t-v_{j-1}^t\right)$
end for
end for

1. 初始化：
   • 每个数据点的初始 Shapley value 设为 0（${\varphi }_i=0$ for $i=1,\dots ,n$ ），并设迭代计数变量 $t$ 从 0 开始（通常，$3n$ 个蒙特卡罗样本是足够收敛的）。
2. 随机排列：
   • 每次迭代中，对整个数据集中的所有数据点进行随机排列，${\pi }^t$ 就是第 $t$ 次迭代中产生的数据点的随机排列。这个排列是随机的，意味着每个数据点都有可能出现在新排列的任何位置，根据排列序列可以确定数据点的加入顺序。
3. 计算边际贡献：
   • 对每次排序中的每个数据点 $i$，计算它在排列 ${\pi }^t$ 中的边际贡献。这通过比较包含数据点 $i$ 之外的所有数据点 $S_{\pi }^i$，和加上数据点 $i$ 后的性能分数差异来实现，即边际贡献/第 $i$ 个数据点的贡献值为：$V(S_{\pi }^i\cup i)-V(S_{\pi }^i)$
4. 计算及更新 Shapley 值：
   • 设定每次迭代的初始性能得分 $v_0^t=V(\varnothing ,\mathcal{A})$，即第 $t$ 次迭代中，不使用任何数据点时模型的性能得分。在第 $t$ 次迭代中，数据点间的排序已经确定，接下来便是依次对 $j=1,2,...n$ 通过 $j-1$ 个数据点的 Shapley 和 $v_t^j-v_t^{j-1}$ 加权计算第 $j$ 个数据点的 Shapley 值。
   • 计算前 $j$ 个数据点的性能得分。$v_t^{j-1}$ 表示在当前迭代 $t$ 中，已经将随机排列 ${\pi }_t$ 中的前 $j-1$ 个数据点纳入模型后的性能得分。若 $|V(D)|-v_{j-1}^t<PerformanceTolerance$，表明第 $j$ 个及以后的所有数据点的性能得分可以忽略不记，可以直接使用 $v_{j-1}^t$ 的估计 $v_t^j$（此处体现了截断 Truncation）。反之，则需输入数据点序列中前 $j$ 个数据点到模型中，计算前 $j$ 个数据点的性能得分 $v_t^j$​​。
   • 加权计算第 $j$ 个数据点的 Shapley 值。${\varphi }_{{\pi }^t[j]}$ : 这是在第 $t$ 次迭代中，数据点 ${\pi }_t^j$ (即当前排列中的第 $j$ 个数据点) 的Shapley值的估计。${\varphi }_{{\pi }^{t-1}[j]}$ : 这是在第 $t-1$ 次迭代中，同一个数据点 ${\pi }_t^j$ 的 Shapley 值的估计。$\frac{t-1}{t}$、$\frac{1}{t}$ : 归一化因子，用于在新旧估计之间进行加权平均，随着 t 值增大，$\frac{t-1}{t}$ 会逐渐增大，也就是旧估计的权重逐渐增大，有助于减少随机波动对 shapley 值的影响，减少对单次迭代结果的以来，使估计结果更加稳定。
5. 重复迭代：
   • 多次生成随机排列，并计算每个数据点的边际贡献，直到达到预定的迭代次数 T 或 Shapley 值收敛。

评价

	优点	缺点
TMC-Shapley	1. 截断策略：通过设置 Performance Tolerance 有效减少计算量 2. 不要求模型可微分	1. 需要大量蒙特卡洛样本 2. 需要大数据集，小数据集会受到随机抽样的影响 3. 计算量仍大

Gradient Shapley, G-Shapley

这种方法特别适用于那些可以通过梯度下降等方法进行训练的模型，如神经网络和支持向量机等。以下是实现基于梯度的方法来计算数据 Shapley 值的步骤：

Input: Parametrized and differentiable loss function $\mathcal{L}(.;\theta )$, train data D = { 1 , … , n } D=\{1, \ldots, n\} D={1,…,n}, performance score function $V(\theta )$
Output: Shapley value of training points: ${\varphi }_1,\dots ,{\varphi }_n$
Initialize ${\varphi }_i=0$ for $i=1,\dots ,n$ and $t=0$
while Convergence criteria not met do
$t\leftarrow t+1$
${\pi }^t$ : Random permutation of train data points
${\theta }_0^t\leftarrow$ Random parameters
$v_0^t\leftarrow V\left({\theta }_0^t\right)$
for j ∈ { 1 , … , n } j \in\{1, \ldots, n\} j∈{1,…,n} do
${\theta }_j^t\leftarrow {\theta }_{j-1}^t-\alpha {\nabla }_{\theta }\mathcal{L}\left({\pi }^t[j];{\theta }_{j-1}\right)$
$v_j^t\leftarrow V\left({\theta }_j^t\right)$
${\varphi }_{{\pi }^t[j]}\leftarrow \frac{t-1}{t}{\varphi }_{{\pi }^{t-1}[j]}+\frac{1}{t}\left(v_j^t-v_{j-1}^t\right)$

​ end for
end for

求解步骤

1. 初始化与随机排列：

   • 每个数据点的初始 Shapley value 设为 0（${\varphi }_i=0$ for $i=1,\dots ,n$），并设迭代计数变量 $t$ 从 0 开始。
   • 第 $t$ 轮迭代，生成一个所有数据点随机排列序列 ${\pi }^t$。
   • 初始化参数 ${\theta }_0^t$，得出模型的性能得分 $V({\theta }_0^t)$，并赋值给 $v_0^t$（表示在第 $t$ 次迭代开始时，不使用任何数据点时模型的性能得分，以便计算第 $j$ 个数据点的边际贡献）。

2. 梯度下降：

   • $\mathcal{L}\left({\pi }^t[j];{\theta }_{j-1}\right)$ 表示在第 $t$ 次迭代中，根据随机排列 ${\pi }_t$ 中的前 $j-1$ 个数据点生成的模型参数 ${\theta }_{j-1}$ 下，第 $j$ 个数据点的损失函数 $\mathcal{L}$ 的值。通过预设的学习率 $\alpha$​，更新参数值。
   • 更新参数后，重新计算前 $j$ 个数据点的贡献值。

3. 加权计算第 j 个数据点的 Shapley value：

   • ${\varphi }_{{\pi }^t[j]}$ : 这是在第 $t$ 次迭代中，数据点 ${\pi }_t^j$ (即当前排列中的第 $j$ 个数据点) 的Shapley值的估计。${\varphi }_{{\pi }^{t-1}[j]}$ : 这是在第 $t-1$ 次迭代中，同一个数据点 ${\pi }_t^j$ 的 Shapley 值的估计。$\frac{t-1}{t}$、$\frac{1}{t}$ : 归一化因子，用于在新旧估计之间进行加权平均，随着 t 值增大，$\frac{t-1}{t}$ 会逐渐增大，也就是旧估计的权重逐渐增大，有助于减少随机波动对 shapley 值的影响，减少对单次迭代结果的以来，使估计结果更加稳定。

4. 重复迭代：

   • 重新迭代，每轮迭代生成一个随机序列 ${\pi }^t$ 并初始化参数 $v_0^t$。计算每个数据点在本轮序列中的 Shapley value。直到达到预定的迭代次数 T 或 Shapley 值收敛。

评价

	优点	缺点
G-Shapley	1. 适用于大型数据集和复杂模型，因为它避免了重复训练的需要，从而显著提高了计算效率。	1. 因为要求骗到，所以要求模型可微分 2.依赖于梯度估计的准确性

---

参考：Data Shapley: Equitable Valuation of Data for Machine Learning（翻译）

Data Shapley ： 机器学习数据的公平估值 ICML2019

代码实现 amiratag/DataShapley: Data Shapley: Equitable Valuation of Data for Machine Learning (github.com)