题目

逆波兰表达式求值

逆波兰表达式就是后缀表达式，我们平时写的带括号的是中缀表达式。区分中缀表达式和后缀表达式 就是 操作数 和 操作符 的先后关系。 操作符在后 就是后缀表达式

• 后缀表达式 的用途就是 让计算机直到计算的先后顺序！
  比如 我们中缀表达式 a * （b - c） 以我们人类的智慧一眼就知道先算后面的括号，是跳跃式的。但是计算机是从左到右扫描整个表达式。所以我们就需要把这个表达式改为其他形式。
• a* （b - c）改成后缀表达式就是 a bc - * 后面的操作符 是根据优先级排的，（）的优先级最高
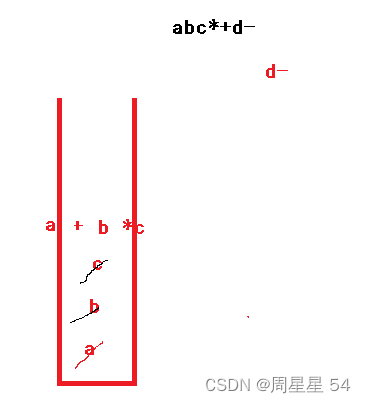
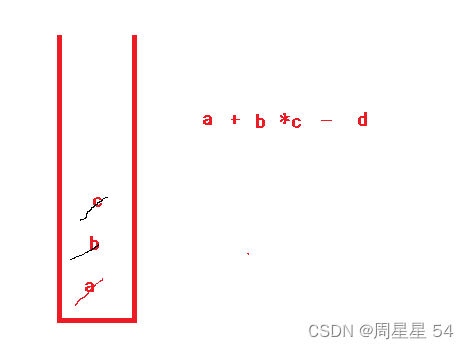
• 再来个例子 a + b * c - d 改成后缀表达式就是 a bc*+d-

算法原理

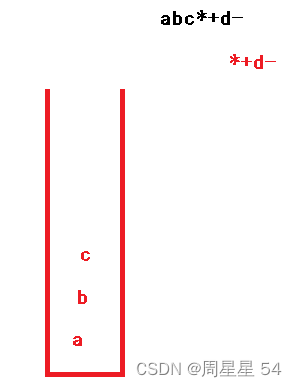
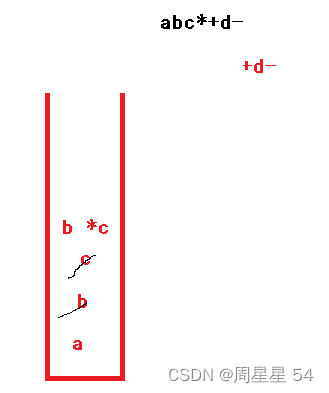
• 先定义一个stack ，遍历数组，遇到数字就入栈
• 遇到操作符就出栈，先出的为右操作数，后出的为左操作数，然后计算的结果再入栈。
• 最后返回栈顶元素就ok了

代码实现

int evalRPN(vector<string>& tokens) {set<string> s = { "+","-","*","/" };stack<int> st;for (auto& str : tokens) {if (s.find(str) != s.end()) {int right = st.top();st.pop();int left = st.top();st.pop();switch (str[0]) {case '+':st.push(left + right);break;case '-':st.push(left - right);break;case '*':st.push(left * right);break;case '/':st.push(left / right);break;}}else {st.push(stoi(str));}}return st.top();
}

可能有同学好奇字符怎么转整型的

补充 stoi的实现

stoi的实现

class Solution {
public:int myAtoi(string str) {int i = 0;while(str[i] == ' '){i++;}int flag = 1;switch (str[i]){case  '-':flag = -1;i++;break;case  '+':flag = 1;i++;break;}//i++;long long ret = 0;for(; i < str.size(); i++){if(str[i]>'9' || str[i]<'0'){break;}ret = 10* ret + (str[i] -'0') ;if(ret > INT_MAX){break;}}ret *= flag;if(ret > INT_MAX){ret = INT_MAX ;}if(ret < INT_MIN){ret = INT_MIN;}return ret ;}
};