1、交叉熵的简单例子

参考文章例子

我们希望通过图像轮廓、颜色等特征，来预测动物的类别，有三种可能类别（猫、狗、猪）假设我们现在有两个模型，都是通过sigmoid/softmax的方式得到的对每个类别预测的概率 。

模型1：
预测 真实 是否正确
0.3 0.3 0.4 0 0 1 (猪) 正确
0.3 0.4 0.3 0 1 0 (狗) 正确
0.1 0.2 0.7 1 0 0 (猫) 错误
模型1对于样本1和样本2以非常微弱的优势判断正确，对于样本3的判断则彻底错误。

模型2：
预测 真实 是否正确
0.1 0.2 0.7 0 0 1 (猪) 正确
0.1 0.7 0.2 0 1 0 (狗) 正确
0.3 0.4 0.3 1 0 0 (猫) 错误
模型2对于样本1和样本2判断非常准确，对于样本3判断错误，但是相对来说没有错得太离谱。

有了模型之后，我们可以定义损失函数来对判断模型在当前样本表现

1.2、Classification Error（分类错误率）

从结果可知，模型1和模型2虽然都是预测错了1个，但是相对来说模型2表现得更好，损失函数值照理来说应该更小，但是，很遗憾的是，classification\ error 并不能判断出来，所以这种损失函数虽然好理解，但表现不太好。

1.3、Mean Squared Error (均方误差)

我们发现，MSE能够判断出来模型2优于模型1，那为什么不采样这种损失函数呢？主要原因是在分类问题中，使用sigmoid/softmx得到概率，配合MSE损失函数时，采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况。

1.4、交叉熵损失函数

交叉熵（Cross Entropy）用于衡量一个概率分布与另一个概率分布之间的距离。
交叉熵是机器学习和深度学习中常常用到的一个概念。在分类问题中，我们通常有一个真实的概率分布（通常是专家或训练数据的分布），以及一个模型生成的概率分布，交叉熵可以衡量这两个分布之间的距离。
模型训练时，通过最小化交叉熵损失函数，我们可以使模型预测值的概率分布逐步接近真实的概率分布。

信息熵
熵 是关于不确定性的数学描述。
信息的大小跟随机事件的概率有关。越小概率的事情发生了产生的信息量越大。
所以 信息的量度应该依赖于概率分布 p ( x ) p(x)p(x)
单调性：发生概率越高的事件，其携带的信息量越低；
非负性：信息熵可以看作为一种广度量，非负性是一种合理的必然；
累加性：即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和，这也是广度量的一种体现

使用python sklearn库实现

from sklearn.metrics import log_loss 
y_true = [[0, 0, 1], [0, 1, 0], [1, 0, 0]] 
y_pred_1 = [[0.3, 0.3, 0.4], [0.3, 0.4, 0.3], [0.1, 0.2, 0.7]] 
y_pred_2 = [[0.1, 0.2, 0.7], [0.1, 0.7, 0.2], [0.3, 0.4, 0.3]] 
print(log_loss(y_true, y_pred_1)) 
print(log_loss(y_true, y_pred_2)) 
____________ 
1.3783888522474517 
0.6391075640678003 

1.5、二分类

回归问题通常用均方差损失函数，可以保证损失函数是个凸函数，即可以得到最优解。而分类问题如果用均方差的话，损失函数的表现不是凸函数，就很难得到最优解。而交叉熵函数可以保证区间内单调。

2、什么是梯度下降法？

参考

梯度下降法在机器学习中常常用来优化损失函数，是一个非常重要的工具。说白了，就是在高中学习过的「极值」的概念，那么什么是极值呢？用非常形象的方式来说极值点，梯度下降法的作用就是寻找一个 「极小值点」，从而让函数的值尽可能地小。相信你也发现了，这么多个极值点，那么梯度下降法找到的是哪一个点呢？关于这个问题就要看运气了，算法的最开始会 「随机」 寻找一个位置然后开始搜索「局部」的最优解，如果运气好的话能够寻找到一个最小值的极值点，运气不好或许找到的就不是最小值的那个极小值点了。

比如说下边儿的这个函数图像 , 可以发现在当前这个区间范围内这个函数有两个极小值点，如果我们想寻找当前函数在这个区间内的最小值点，那么当然是第二个极小值点更合适一些，可是并不一定能够如我们所愿顺利地找到第二个极小值点，这时候只能够通过多次尝试。

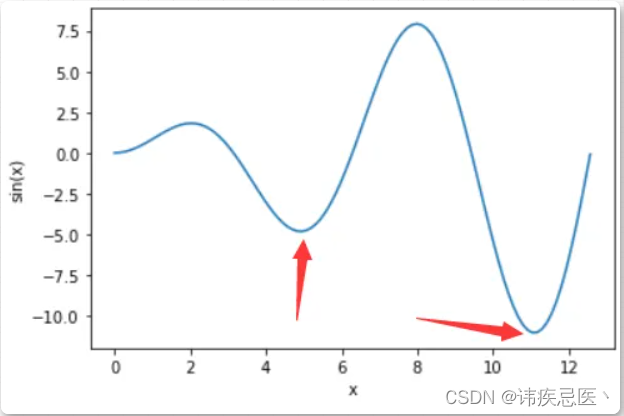
2.2、梯度下降法的运行过程

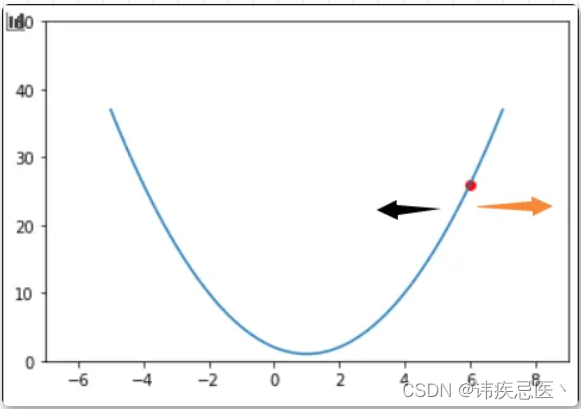
接下来用一个简单的一元二次函数来阐述算法的运行过程。一元二次函数天生地就只有一个极小值点，方便用来说明问题。函数的表达式是 f(x) = (x-1)^2+1,通过表达式可以知道它的最小值点的坐标是(1,1)

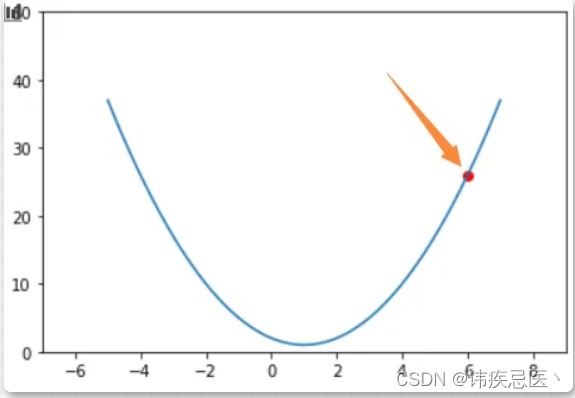
「梯度的概念」：梯度就是函数对它的各个自变量求偏导后，由偏导数组成的一个向量。
「梯度下降法」:每个自变量方向上的偏导数构成的向量，函数f(x) 的梯度就是f(x)’ = 2x-2

图上有一个小红点，它的坐标是 (6, f(6)), 也就是当x=6的时候二次函数曲线上边儿的点。那么也可以得到f(6)'=10，也就是这个红点的位置的导数是等于10的。现在用导数值的 「正负来表示方向」，如果导数的值是正数，那么就代表x轴的正方向。如果导数的值是负数，那么就代表是x轴的负方向。那么你会发现，知道了这个方向之后也就知道了应该让f(x)往哪个方向变化x的值才会增大。如果想要让f(x)的值减小，那么就让x朝着导数告诉我们的方向的反方向变化就好啦。接下来我用「黄色」箭头代表导数告诉我们的方向，用「黑色」箭头代表导数指向的方向的反方向。

「梯度下降法」 的目标是搜索出来一个能够让函数的值尽可能小的位置，所以应该让x朝着黑色箭头的方向走，那么怎么完成这个操作呢?
在代码中有一个eta变量，它的专业名词叫 「学习率」。使用数学表达式来表示更新

表达式的意思就是让x减去eta乘以函数的导数。其中的eta是为了控制x更新的幅度，将eta设置的小一点，那么每一次更新的幅度就会小一点。

初始化

# 变量 x 表示当前所在的位置
# 就随机初始在 6 这个位置好了
x = 6
eta = 0.05

第一次更新x

# 变量 df 存储当前位置的导数值
df = 2*x-2
x = x - eta*df
# 更新后 x 由 6 变成 
# 6-0.05*10 = 5.5

第二次更新x

# 因为 x 的位置发生了变化
# 要重新计算当前位置的导数
df = 2*x-2
x = x - eta*df
# 更新后 x 由 5.5 变成
# 5.5-0.05*9 = 5.05

接下来只要重复刚才的过程就可以了。那么，把刚才的两个步骤画出来。其中红色箭头指向的点是初始时候的点，「黄色」 箭头指向的点是第 1 次更新后的位置，「蓝色」 箭头指向的点是第 2 次更新后的位置。

只要不停地重复刚才的这个过程，那么最终就会收敛到一个 「局部」 的极值点。那么可以想一下这是为什么？因为随着每一次的更新，曲线都会越来越平缓，相应的导数值也会越来越小，当我们接近极值点的时候导数的值会无限地靠近 「0」。由于导数的绝对值越来越小，那么随后更新的幅度也会越来越小，最终就会停留在极值点的位置了。接下来我将用 Python 来实现这个过程，并让刚才的步骤迭代 1000 次。

import matplotlib.pyplot as plt
import numpy as np# 初始算法开始之前的坐标 
# cur_x 和 cur_y 
cur_x = 6
cur_y = (cur_x-1)**2 + 1
# 设置学习率 eta 为 0.05
eta = 0.05
# 变量 iter 用于存储迭代次数
# 这次我们迭代 1000 次
# 所以给它赋值 1000
iter = 1000
# 变量 cur_df 用于存储
# 当前位置的导数
# 一开始我给它赋值为 None
# 每一轮循环的时候为它更新值
cur_df = None# all_x 用于存储
# 算法进行时所有点的横坐标
all_x = []
# all_y 用于存储
# 算法进行时所有点的纵坐标
all_y = []# 把最一开始的坐标存储到
# all_x 和 all_y 中
all_x.append(cur_x)
all_y.append(cur_y)# 循环结束也就意味着算法的结束
for i in range(iter):# 每一次迭代之前先计算# 当前位置的梯度 cur_df# cur 是英文单词 current cur_df = 2*cur_x - 2# 更新 cur_x 到下一个位置cur_x = cur_x - eta*cur_df# 更新下一个 cur_x 对应的 cur_ycur_y = (cur_x-1)**2 + 1# 其实 cur_y 并没有起到实际的计算作用# 在这里计算 cur_y 只是为了将每一次的# 点的坐标存储到 all_x 和 all_y 中# all_x 存储了二维平面上所有点的横坐标# all_y 存储了二维平面上所欲点的纵坐标# 使用 list 的 append 方法添加元素all_x.append(cur_x)all_y.append(cur_y)# 这里的 x, y 值为了绘制二次函数
# 的那根曲线用的，和算法没有关系
# linspace 将会从区间 [-5, 7] 中
# 等距离分割出 100 个点并返回一个
# np.array 类型的对象给 x
x = np.linspace(-5, 7, 100)
# 计算出 x 中每一个横坐标对应的纵坐标
y = (x-1)**2 + 1
# plot 函数会把传入的 x, y
# 组成的每一个点依次连接成一个平滑的曲线
# 这样就是我们看到的二次函数的曲线了
plt.plot(x, y)
# axis 函数用来指定坐标系的横轴纵轴的范围
# 这样就表示了 
# 横轴为 [-7, 9]
# 纵轴为 [0, 50]
plt.axis([-7, 9, 0, 50])
# scatter 函数是用来绘制散点图的
# scatter 和 plot 函数不同
# scatter 并不会将每个点依次连接
# 而是直接将它们以点的形式绘制出来
plt.scatter(np.array(all_x), np.array(all_y), color='red')
plt.show()

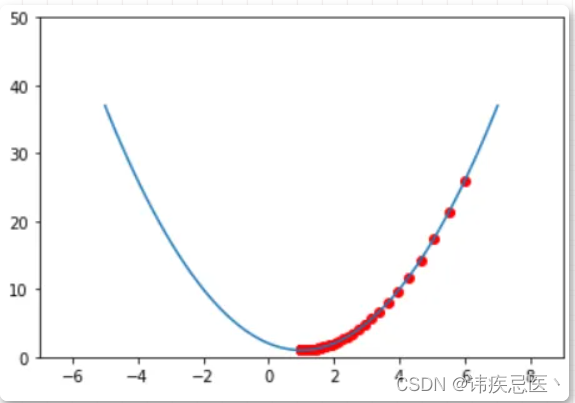
通过最终的效果图可以发现，「梯度下降」在一步一步地收敛到二次函数的极小值点，同时也是二次函数的最小值点。仔细看一下，可以发现，就像刚才提到的，随着算法的运行，红色的点和点之间的距离越来越小了，也就是每一次更新的幅度越来越小了。这可不关「学习率」 的事儿，因为在这里用到的学习率是一个固定的值，这只是因为随着接近极值点的过程中「导数的绝对值」越来越小。
同时，我们还可以把 all_x 和 all_y 中最后一个位置存储的值打印出来看一下，如果没错的话，all_x 的最后一个位置的值是接近于 1 的，同时对应的函数值 all_y 最后一个位置的值也应该是接近于 1 的。

2.3、二元函数的梯度下降

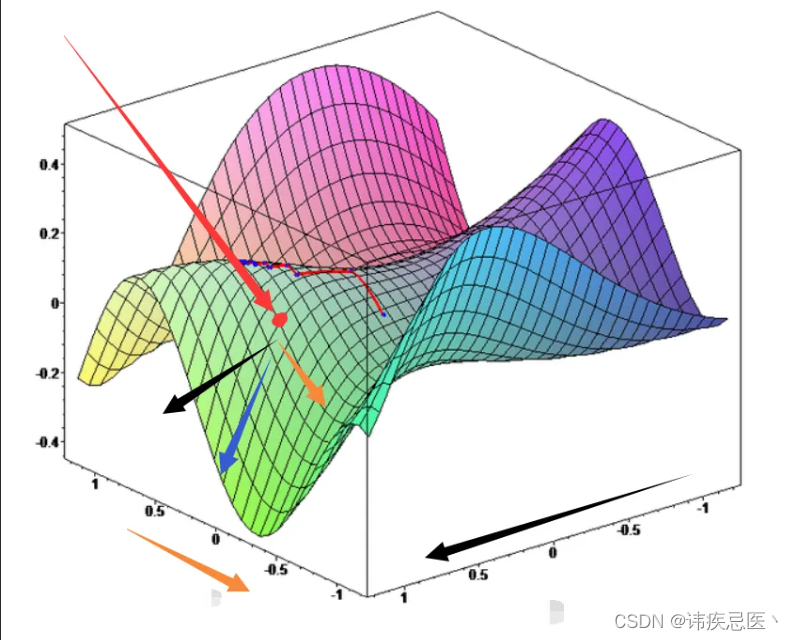
在多元函数中拥有多个自变量，在这里就用二元的函数来举例子好了，二元函数的图像是在三维坐标系中的。下边儿就是一个多元函数的图像例子。在这里纵坐标我使用 「y」 表示，底面的两个坐标分别使用 「x1」 和 「x2」 来表示。不用太纠结底面到底哪个轴是 x1 哪个轴是 x2，这里只是为了说明问题。

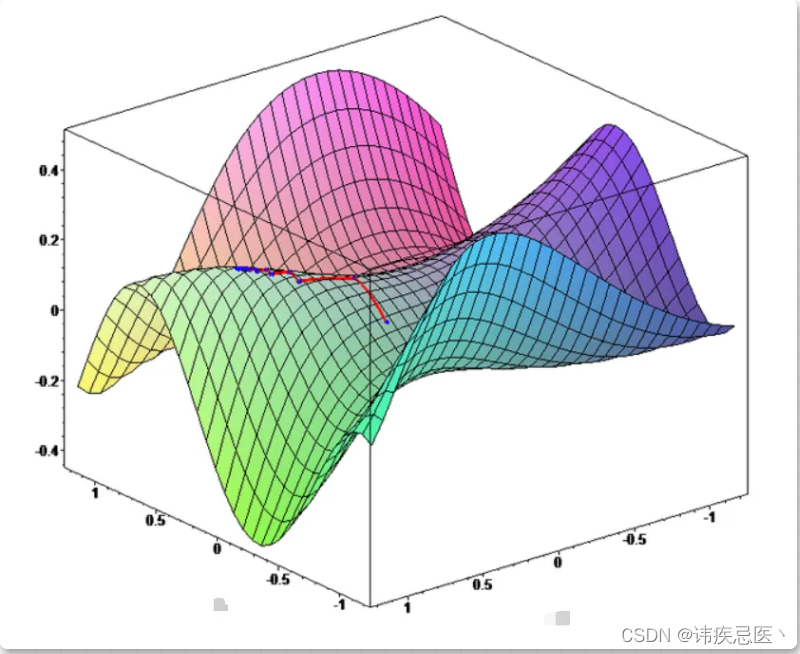
通过上面的二元函数凸显可以发现想要让 「y」 的值尽可能地小就要寻找极值点（同样地这个极值点也不一定是最小值点）。梯度是一个由各个自变量的偏导数所组成的一个「向量」。用数学表达式看上去就是下边儿这样的。

同样地，一开始随机初始一个位置，随后让当前位置的坐标值减去学习率乘以当前位置的偏导数。更新自变量 x1 就让 x1 减去学习率乘以 y 对 x1 的偏导数，更新自变量 x2 就让 x2 减去学习率乘以 y 对 x2 的偏导数。

发挥想象力再思考一下，既然梯度是一个向量，那么它就代表了一个方向。x1 的偏导数的反方向告诉我们在 x1 这个轴上朝向哪个方向变化可以使得函数值 y 减小，x2 的偏导数的反方向告诉我们在 x2 这个轴上朝向哪个方向变化可以使得函数值 y 减小。那么，由偏导数组成的向量就告诉了我们在底面朝向哪个方向走就可以使得函数 y 减小。
在下边儿的图中，我使用红色箭头表示我们当前所在的位置，随后我使用 「黑色」 箭头代表其中一个轴上的坐标朝向哪个方向变化可以使得函数值 「y」 减小，并使用 「黄色」 箭头代表另外一个轴上的坐标朝向哪个方向变化可以使得函数值 「y」 减小。根据平行色变形法则有了 「黑色」 向量和 「黄色」 向量，就可以知道这两个向量最终达到的效果就是 「蓝色」 向量所达到的效果。

最终，对于二元函数梯度下降的理解，就可以理解为求出的梯度的反方向在底面给了我们一个方向，只要朝着这个方向变化底面的坐标就可以使得函数值 「y」 变小。