1、算法描述

4FSK在频移键控（FSK）编码的基础上有所扩展。FSK是一种调制技术，它通过在不同频率上切换来表示不同的数字或符号。而4FSK则是FSK的一种变种，表示使用了4个不同的频率来传输信息。

在4FSK中，每个数字或符号被映射到一组连续的四个频率中的一个。这些频率通常以二进制编码的形式进行表示，例如00、01、10和11。每个频率组合对应于不同的数字或符号。因此，通过在这四个频率之间进行切换，我们可以传输数字数据。

4FSK在一些通信系统中用于数据传输，因为它可以在有一定噪声干扰的情况下提供较好的抗干扰性能。然而，需要注意的是，频率越多，理论上可以传输的信息速率也越高，但同时也需要更宽的频谱带宽。

当使用4FSK进行数据传输时，发送端将要传输的数字数据映射到相应的频率组合，并以这些频率的序列形式发送。接收端则需要解码接收到的频率序列，将其转换回原始的数字数据。

4FSK的优点之一是其相对较高的抗干扰性能。因为它使用多个频率来表示不同的数字或符号，即使在信号中存在一些噪声或干扰，接收端仍然可以正确地解码出数据。这使得4FSK在无线通信、调制解调器、无线传感器网络等领域得到了广泛的应用。

需要注意的是，4FSK并不是唯一的调制技术，还有许多其他的调制方式，如二进制频移键控（BFSK）、正交频分复用（OFDM）等。选择适当的调制方式取决于通信环境、带宽要求以及抗干扰性能等因素。

总之，4FSK是一种通过在不同的频率上切换来传输数字数据的调制技术，它在某些情况下可以提供较好的抗干扰性能，适用于许多无线通信应用中。

以下是一些与其相关的基本公式：

1. **频率与码元之间的关系：**
   
   在4FSK中，每个码元（symbol）对应于一组连续的4个频率中的一个。假设码元持续时间为 T。

   - 基本频率：f₀
   - 第一个频率：f₁ = f₀ + Δf
   - 第二个频率：f₂ = f₀ + 2Δf
   - 第三个频率：f₃ = f₀ + 3Δf

   其中，Δf 是频率间隔。

2. **码元速率：**

   码元速率是指每秒传输的码元数量，通常以 baud 或 symbols per second（sps）来表示。

   - 码元速率 = 1 / T

3. **数据速率：**

   数据速率是指每秒传输的二进制位数（bps）。

   - 数据速率 = 码元速率 × 每个码元的比特数

4. **信号频率的相位：**

   在相移键控调制中，相位的变化表示不同的信号状态。相位差 Δφ 可以通过以下公式计算：

   - Δφ = 2πΔfT

   其中，Δf 是频率间隔，T 是码元持续时间。
 

2、仿真结果演示

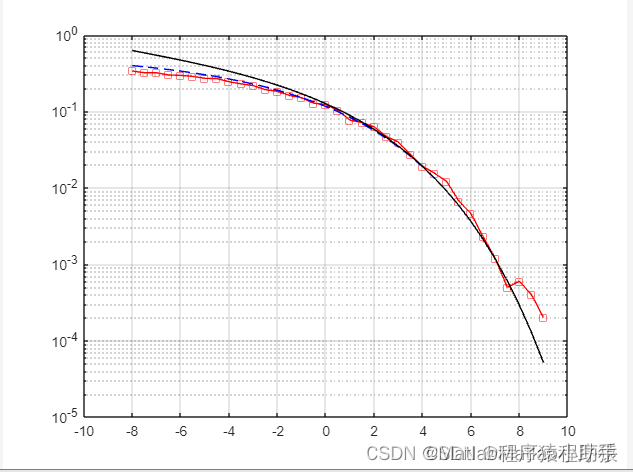
3、关键代码展示

略

4、MATLAB 源码获取

点击下方原文链接获取

【MATLAB源码-第12期】基于matlab的4FSK（4CPFSK）的误码率BER理论值与实际值仿真。-CSDN博客https://blog.csdn.net/Koukesuki/article/details/132326939?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171245840716777224418873%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=171245840716777224418873&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-132326939-null-null.nonecase&utm_term=%E7%AC%AC12%E6%9C%9F&spm=1018.2226.3001.4450