n 皇后问题
研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
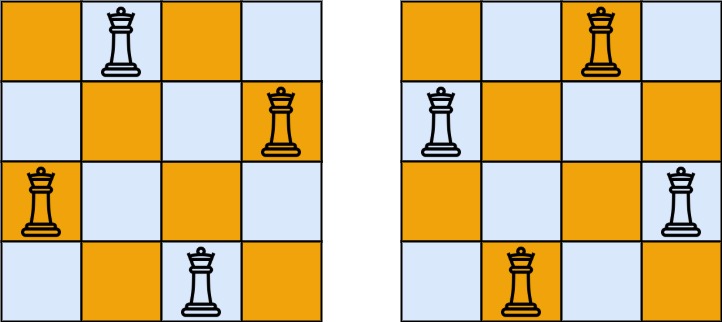
输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 9
代码如下链接,也可以看下文,大家请帮忙点赞,收藏,谢谢。
N皇后en.lua ![]() https://gitcode.com/funsion/CLua/blob/master/%E8%93%9D%E6%A1%A5%E6%9D%AFlua%E4%B8%AD%E6%96%87%E8%A7%A3%E6%B3%95/N%E7%9A%87%E5%90%8Een.luaN皇后中文.lua
https://gitcode.com/funsion/CLua/blob/master/%E8%93%9D%E6%A1%A5%E6%9D%AFlua%E4%B8%AD%E6%96%87%E8%A7%A3%E6%B3%95/N%E7%9A%87%E5%90%8Een.luaN皇后中文.lua ![]() https://gitcode.com/funsion/CLua/blob/master/%E8%93%9D%E6%A1%A5%E6%9D%AFlua%E4%B8%AD%E6%96%87%E8%A7%A3%E6%B3%95/N%E7%9A%87%E5%90%8E%E4%B8%AD%E6%96%87.lua
https://gitcode.com/funsion/CLua/blob/master/%E8%93%9D%E6%A1%A5%E6%9D%AFlua%E4%B8%AD%E6%96%87%E8%A7%A3%E6%B3%95/N%E7%9A%87%E5%90%8E%E4%B8%AD%E6%96%87.lua
解题思路如下:
1. 初始化棋盘
首先,我们创建一个大小为 n×n 的二维数组(即“棋盘”),其中每个元素初始值为假,表示该位置尚未放置皇后。这样就构建了一个空白的棋盘模型。
2. 回溯算法
使用回溯算法来搜索所有可能的皇后放置方案。回溯算法是一种递归地尝试解决问题的方法,当发现当前路径不可行时,会退回至上一步状态,尝试其他可能性。在这个问题中,我们从棋盘的第一行开始,逐行尝试在每一列放置皇后。具体步骤如下:
- 当放置完 n 个皇后(即行数达到 n)时,找到一个解,将当前棋盘状态添加到解法集中。
- 对于当前行,遍历所有列,检查在该列放置皇后是否安全。若安全,则在该位置放置皇后,并递归地进入下一行继续放置皇后。
- 若在下一行无法继续放置皇后(即所有列都不安全),则回溯至上一行的前一列,尝试在该列放置皇后。
- 当回溯至第一行仍无法找到安全的列放置皇后时,说明当前路径无法生成有效解,需要返回至上一层递归,撤销上一行最后一个皇后的位置,然后尝试其前一列。
3. 安全性判断
判断某一位置(行 r,列 c)是否可以安全放置皇后,需满足以下三个条件:
- 当前列(c)上无皇后:检查从第一行到当前行(r-1)的所有同列位置,确保无皇后。
- 左上到右下对角线上无皇后:计算该对角线的起始列(c - r + 1),检查从第一行到当前行(r-1)的所有同对角线位置,确保无皇后。
- 右上到左下对角线上无皇后:计算该对角线的起始列(c + r - 1),检查从第一行到当前行(r-1)的所有同对角线位置,确保无皇后。
只有当这三个条件都满足时,该位置才被视为安全,可以放置皇后。
4. 输出解集
最后,遍历解法集中存储的所有解(即棋盘状态),并输出它们。这些解即为 n 皇后问题的所有有效解。
综上所述,这段代码通过初始化棋盘、采用回溯算法搜索解空间、判断皇后放置安全性以及输出解集,有效地解决了 n 皇后问题。
如果要输出解法数量怎么写呢?请评论区回复。
函数 解皇后(n)局部 空棋盘 = {} -- 初始化一个空棋盘因为 i = 1, n 做空棋盘[i] = {}因为 j = 1, n 做空棋盘[i][j] = 假 -- 初始状态下,每个格子都没有皇后结束结束局部 解法集 = {} -- 存放所有解的容器局部 函数 回溯(行)如果 行 > n 即 -- 如果已经放置了 N 个皇后,找到一个解局部 行内容 = ""因为 r = 1, n 做因为 c = 1, n 做行内容 = 行内容 .. (空棋盘[r][c] 与 "凤 " 或 "囗 ")结束行内容 = 行内容 .. "\n"结束表.insert(解法集, 行内容)返回结束因为 列 = 1, n 做 -- 依次尝试在当前行的每个列放置皇后如果 安全吗(行, 列, 空棋盘) 即空棋盘[行][列] = 真 -- 放置皇后回溯(行 + 1) -- 继续在下一行放置皇后空棋盘[行][列] = 假 -- 回溯:撤销当前行的皇后放置结束结束结束函数 安全吗(行, 列, 空棋盘)-- 检查当前列是否有皇后因为 r = 1, 行 - 1 做如果 空棋盘[r][列] 即返回 假结束结束-- 检查左上到右下的对角线是否有皇后局部 左上对角线 = 列 - 行 + 1因为 r = 1, 行 - 1 做局部 c = 左上对角线 + r如果 c <= n 与 空棋盘[r][c] 即返回 假结束结束-- 检查右上到左下的对角线是否有皇后局部 右上对角线 = 列 + 行 - 1因为 r = 1, 行 - 1 做局部 c = 右上对角线 - r如果 c >= 1 与 空棋盘[r][c] 即返回 假结束结束返回 真 -- 当前位置可以安全放置皇后结束回溯(1) -- 从第一行开始放置皇后返回 解法集
结束-- 示例:求解 4 皇后问题
局部 解法集 = 解皇后(4)
因为 _, 解法 属于 序配(解法集) 做输出(解法)
结束表格还没完成汉化,所以还是用英文 。
这段代码运行后将会输出:
凤 囗 囗 囗
囗 凤 囗 囗
囗 囗 凤 囗
囗 囗 囗 凤--------------
凤 囗 囗 囗
囗 囗 囗 凤
囗 囗 凤 囗
囗 凤 囗 囗--------------
囗 凤 囗 囗
凤 囗 囗 囗
囗 囗 囗 凤
囗 囗 凤 囗--------------
囗 凤 囗 囗
囗 囗 凤 囗
囗 囗 囗 凤
凤 囗 囗 囗--------------
囗 囗 凤 囗
囗 凤 囗 囗
凤 囗 囗 囗
囗 囗 囗 凤--------------
囗 囗 凤 囗
囗 囗 囗 凤
凤 囗 囗 囗
囗 凤 囗 囗--------------
囗 囗 囗 凤
凤 囗 囗 囗
囗 凤 囗 囗
囗 囗 凤 囗--------------
囗 囗 囗 凤
囗 囗 凤 囗
囗 凤 囗 囗
凤 囗 囗 囗








![[Mac]安装App后“XX已损坏,无法打开“](https://img-blog.csdnimg.cn/direct/1c853bec01454fe48d87bbfa5f35f91e.png)