文章目录
顺序表基本操作实现
知识总览
1.顺序表的初始化
1.1静态分配顺序表的初始化
1.2动态分配顺序表的初始化
2.插入操作
2.1插入操作流程
2.2插入操作时间复杂度
3.删除操作
3.1删除操作流程
3.2删除操作时间复杂度
4.查找操作
4.1按位查找
4.2按位查找时间复杂度
4.3按值查找(顺序查找)
4.4按值查找时间复杂度
知识回顾与重要考点
顺序表基本操作实现
知识总览
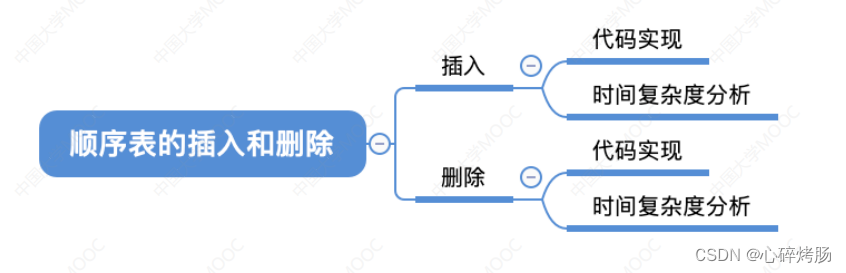
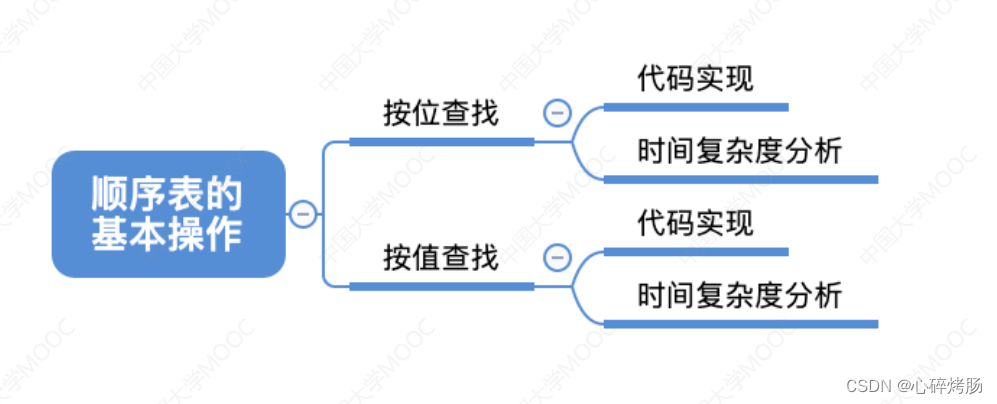
注意
在各种操作的实现中(包括严蔚敏老师撰写的教材),往往可以忽略边界条件判断、变量定义、内存分配不足等细节,即不要求代码具有可执行性,而重点在于算法的思想。
1.顺序表的初始化
静态分配和动态分配的顺序表的初始化操作是不同的。
1.1静态分配顺序表的初始化
静态分配在声明一个顺序表时,就已为其分配了数组空间,因此初始化时只需将顺序表的当前长度设为0。
//SqList L; //声明一个顺序表
void InitList(SqList &L){L.length=0; //顺序表初始长度为0}
1.2动态分配顺序表的初始化
动态分配的初始化为顺序表分配一个预定义大小的数组空间,并将顺序表的当前长度设为0。MaxSize指示顺序表当前分配的存储空间大小,一旦因插入元素而空间不足,就进行再分配。
void InitList(SeqList &L){L.data= (ElemType *)malloc (MaxSize*sizeof(ElemType)); //分配存储空间L.length=0; //顺序表初始长度为0L. MaxSize=InitSize; //初始存储容量
}2.插入操作
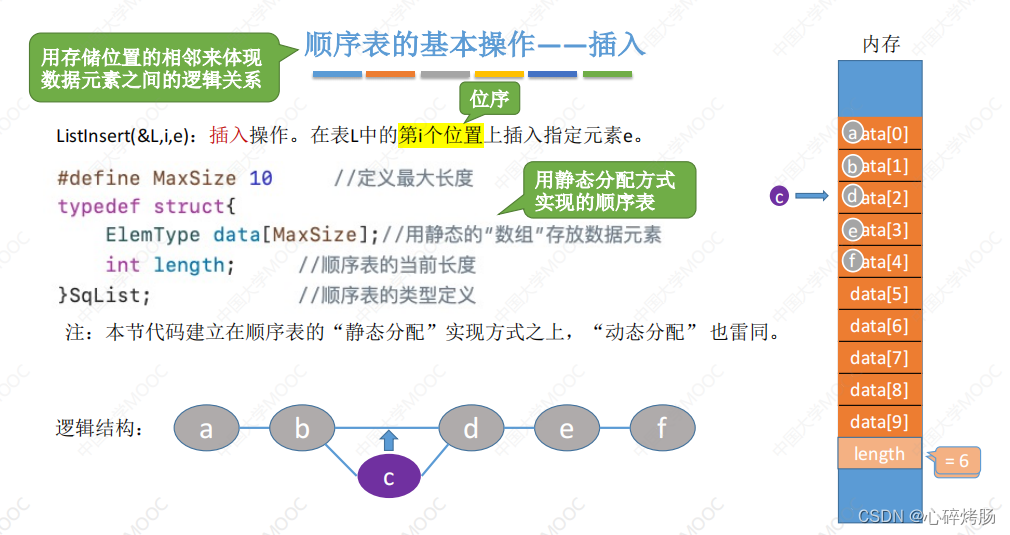
2.1插入操作流程
在顺序表L的第i(1<=i<=L.length+1)个位置插入新元素e。
若i的输入不合法,则返回false,表示插入失败;
否则,将第i个元素及其后的所有元素依次往后移动一个位置,腾出一个空位置插入新元素e,顺序表长度增加1,插入成功,返回true。
bool ListInsert(SqList &L,int i,ElemType e){if(i<1|i>L.length+1) //判断i的范围是否有效return false;if(L.length>=MaxSize) //当前存储空间已满,不能插入return false;for(int j=L.length;j>=i;j--) //将第i个元素及之后的元素后移L.data[j]=L.data[j-1];L.data[i-1]=e; //在位置i处放入eL.length++; //线性表长度加1return true;
}
注意
区别顺序表的位序和数组下标。为何判断插入位置是否合法时if语句中用length+1,而移动元素的for语句中只用length?


2.2插入操作时间复杂度
最好情况:在表尾插入(即i=n+1),元素后移语句将不执行,时间复杂度为O(1)。
最坏情况:在表头插入(即i= 1),元素后移语句将执行n次,时间复杂度为O(n)。
平均情况:假设pi (pi=1/(n+1))是在第i个位置上插入一个结点的概率,则在长度为n的线性表中插入一个结点时,所需移动结点的平均次数为
因此,顺序表插入算法的平均时间复杂度为O(n)。

3.删除操作
3.1删除操作流程
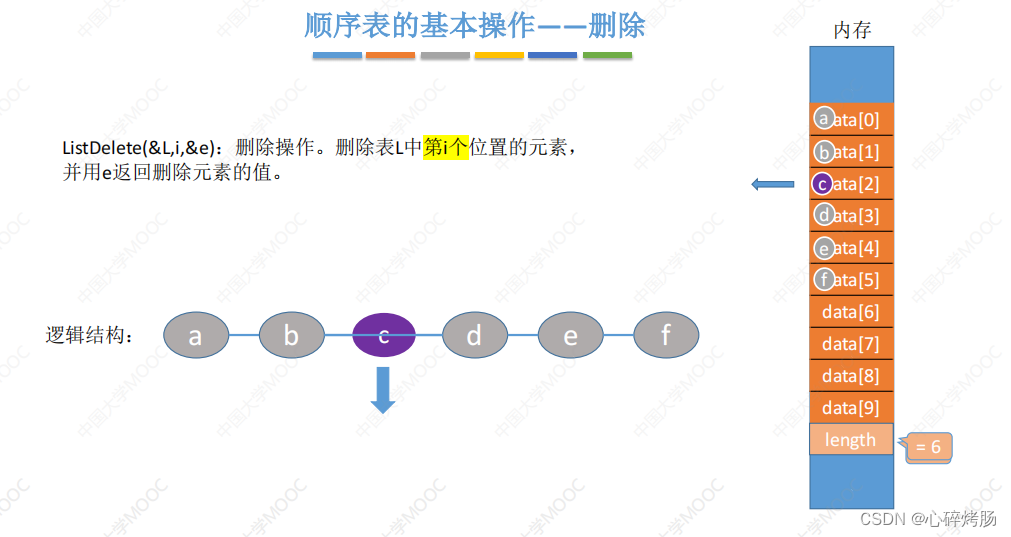
删除顺序表L中第i(1<=i<=L.length)个位置的元素,用引用变量e返回。若i的输入不合法,则返回false;否则,将被删元素赋给引用变量e,并将第i+1个元素及其后的所有元素依次往前移动一个位置,返回true.
bool ListDelete(SqList &L,int i, ElemType &e){if(i<1 || i>L.length) //判断i的范围是否有效return false;e=L.data[i-1]; //将被删除的元素赋值给efor(int j=i;j<L.length;j++) //将第i个位置后的元素前移L.data[j-1]=L.data[j];L.length--; //线性表长度减1return true;
}
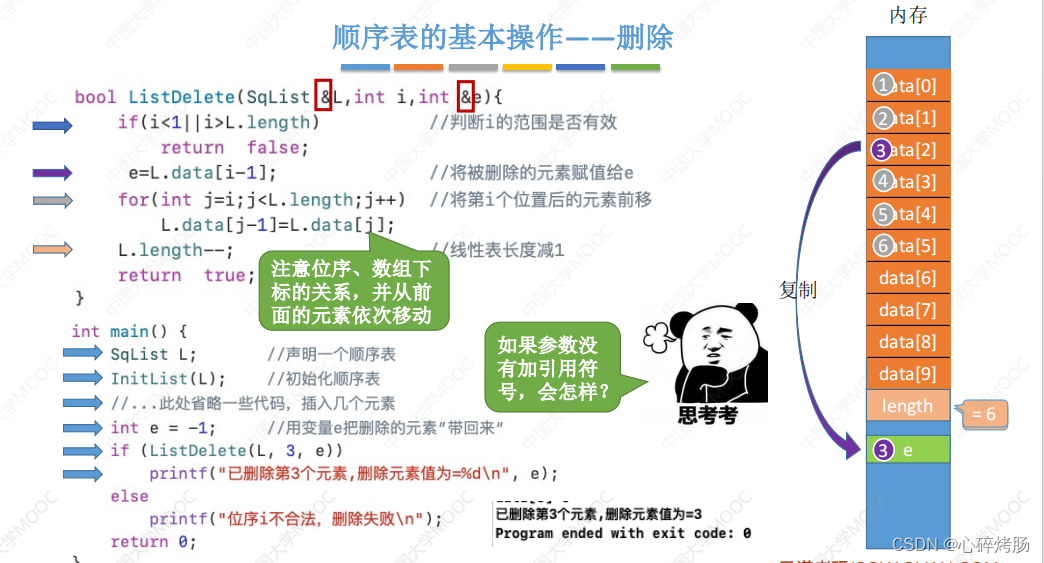
3.2删除操作时间复杂度
最好情况:删除表尾元素(即i=n),无须移动元素,时间复杂度为O(1)。
最坏情况:删除表头元素(即i=1),需移动除表头元素外的所有元素,时间复杂度为O(n)
平均情况:假设pi(pi =1/n)是删除第i个位置上结点的概率,则在长度为n的线性表中删除一个结点时,所需移动结点的平均次数为
因此,顺序表删除算法的平均时间复杂度为O(n)。
可见,顺序表中插入和删除操作的时间主要耗费在移动元素上,而移动元素的个数取决于插入和删除元素的位置。
4.查找操作
4.1按位查找


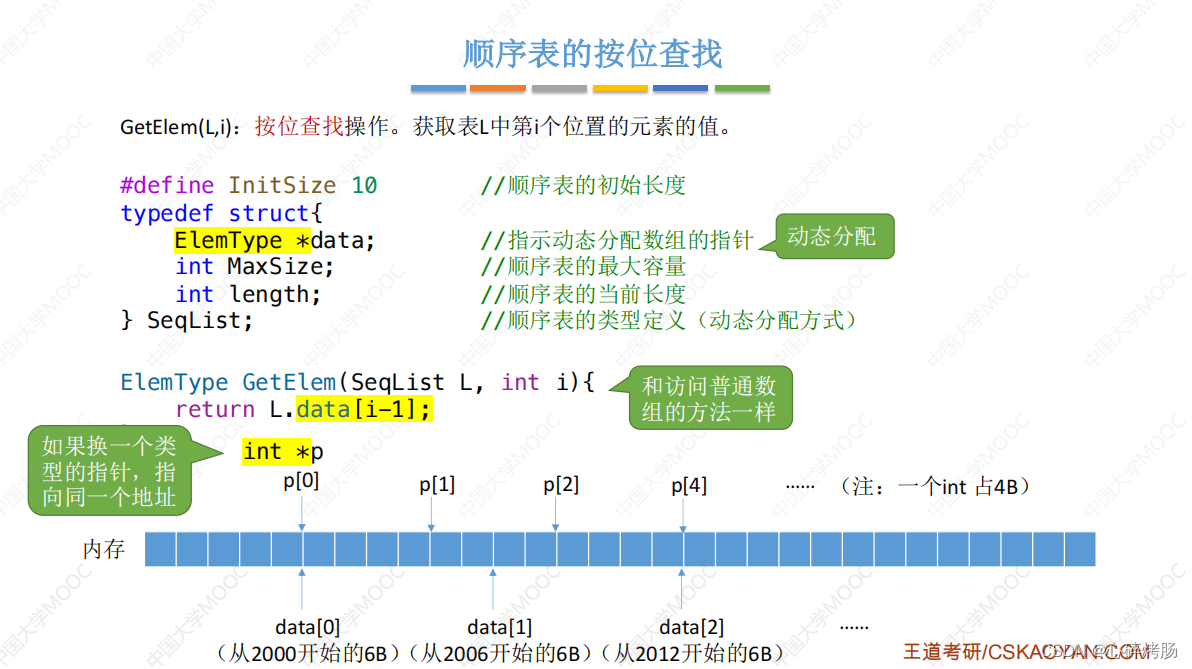

4.2按位查找时间复杂度

4.3按值查找(顺序查找)
在顺序表L中查找第一个元素值等于e的元素,并返回其位序。
int LocateE lem (SqList L,ElemType e){int i;for(i=0;i<L.length;i++)if(L.data [i]==e)return i+1; //下标为i的元素值等于e,返回其位序i+1return 0; //退出循环,说明查找失败
}




4.4按值查找时间复杂度
最好情况:查找的元素就在表头,仅需比较一次,时间复杂度为O(1)。
最坏情况:查找的元素在表尾(或不存在)时,需要比较n次,时间复杂度为O(n)。
平均情况:假设pi (pi=1/n)是查找的元素在第i (1<=i<=L.length)个位置上的概率,则在长度为n的线性表中查找值为e的元素所需比较的平均次数为
因此,顺序表按值查找算法的平均时间复杂度为O(n)。
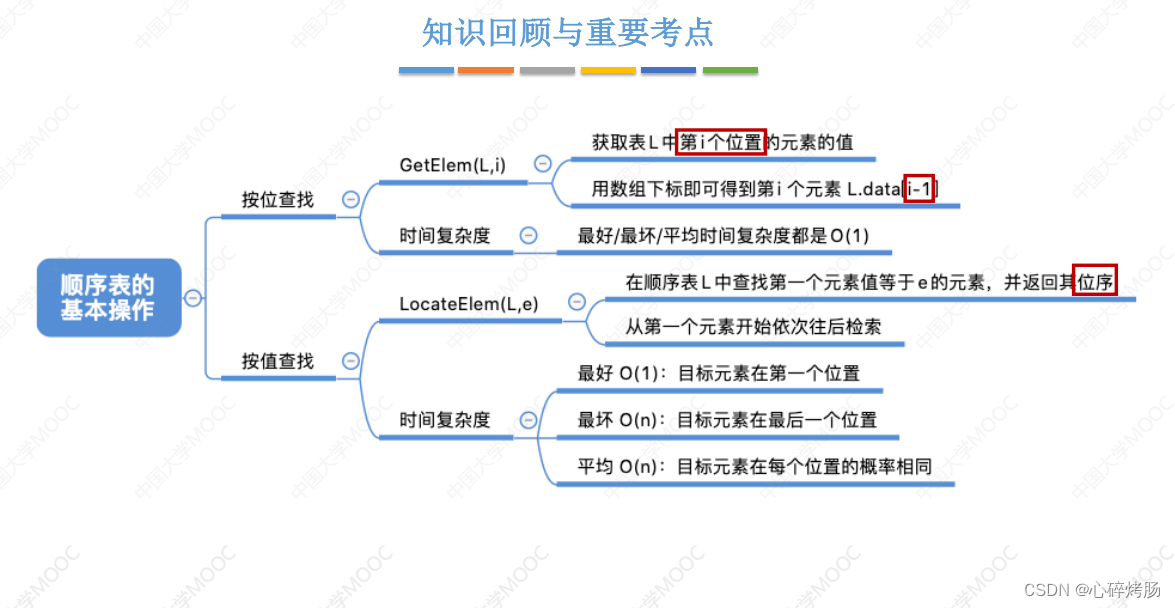
知识回顾与重要考点



![P8786 [蓝桥杯 2022 省 B] 李白打酒加强版](https://img-blog.csdnimg.cn/direct/8ea1b0a566b849b8bceed2efacec159d.png)