深度学习中的temperature parameter是什么
问题来源
在google的论文《Sampling-Bias-Corrected Neural Modeling for Large Corpus Item Recommendations》中看到这个公式:

对于这个t很好奇。 先简单介绍一下这篇论文,用双塔做推荐,左侧是user特征,右侧是item特征,然后通过DNN之后得到对应向量,再求向量内积得到一个数表示二者相关程度,计算出user和正类item和负类item的相关程度的数值之后,再通过softmax函数,得到user点击每个item的概率值。假设我们有1个正类2个负类,那么我们会将如下向量输入softmax layer:

这里x代表user向量,y代表item向量。 一般来说,我们直接求内积就得到了s(x,y),为什么还要除以t呢?这个t是什么,有什么作用呢?
temperature parameter
这个t叫做温度参数,我们加入到softmax中看看会有什么效果。假设我们处理的是一个三分类问题,模型的输出是一个3维向量:
[1,2,3]
然后计算交叉熵损失,首先我们要通过一个softmax layer,softmax公式大家都很熟悉:

我们得到结果:
[0.09003057317038046, 0.24472847105479767, 0.6652409557748219]
我们让t=2,其实也就是让[1/2,2/2,3/2]计算softmax,得到结果:
[0.1863237232258476, 0.30719588571849843, 0.506480391055654]
再让t=0.5,让[1/0.5,2/0.5,3/0.5]计算softmax,得到结果:
[0.015876239976466765, 0.11731042782619835, 0.8668133321973348]
看到区别了吗,t越大,结果越平滑,让本来t=1时大的结果变小一点,小的变大一点,得到的概率分布更“平滑”,相应的t越小,得到的概率分布更“尖锐”,这就是t的作用。
如何使用
t的大小和模型最终模型的正确率没有直接关系,我们可以将t的作用类比于学习率。我们的label类似于[1,0,0],最“尖锐”,如果我们在训练时将t设置比较大,那么预测的概率分布会比较平滑,那么loss会很大,这样可以避免我们陷入局部最优解。随着训练的进行,我们将t变小,也可以称作降温,类似于模拟退火算法,这也是为什么要把t称作温度参数的原因。变小模型才能收敛。比如我们可以这这样设置t:
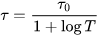
这里的T表示的是训练循环的次数。
在这篇论文中,设置的是固定的t,并没有进行降温的过程,并且t=0.05比较小,我试了一下,loss下降很快。我觉得可能跟使用场景有关,因为这篇文章的label都是[1,0,0],正类总在第一位。