多因子模型的数据处理

优质博文：IT-BLOG-CN
在这里插入图片描述

数据处理的基本目的是从多量的、可能是杂乱无章的、难以理解的数据中抽取并推导出有价值、有意义的数据。特别是金融数据，存在数据缺失，不完整以及极端异常值等问题，对于我们的分析和建模影响很多。

对于我们分析多因子模型来说，我们进行数据处理主要有以下两个原因：
【1】原始数据使用到因子中会存在很多杂音，对于我们进行因子分析有很多的影响，
【2】各因子结合在一起来分析模型的主动收益时，要求各因子数据的分布要相互匹配（类似的分布）。

首先，我们先处理极端异常值Outliers，处理异常值的方法有成千上万种，其中我们使用最多并且非常有效的方法是如下公式：
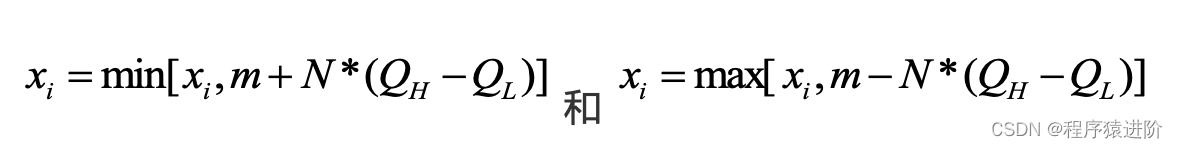
在这里插入图片描述

以上两个公式分别决定了数据的上限和下限，其中N常取2或3，分别是将全部数据从小到多排序75%，25%百分率对应的数据值，m是整列数据的中位数。

按照如上方法处理完异常值后，需检验我们的数据是否充分处理。我们检验的标准是：先计算经处理数据的偏度Skewness，然后再随机去除掉5%-10%的数据，重新计算偏度Skewness，如果两者的偏度偏差不多，那举说明我们的数据进行了充分的裁剪。

然后，我们还需要对各个裁剪完的因子数据进行分布转换。通常我们希望选取因子的分布尽量呈现正态分布，而金融数据通常呈现右偏分布且具有非负性，所以我们通常采用对数转换来处理我们选取的因子数据。其他处理方法还有对数据进行平方、开方、开方，或者使用平滑异同移动平均线来对数据进行正态分布化处理。

总而言之，我们不需要选取因子的分布呈现标准正态分布，我们叧需因子的数据看起来大致呈现正态分布。

假如我们使用了以上方法，但是因子数据仍然没有呈现明显的正态分布，我们还有以下几种方法来对数据进行处理：
【1】对因子进行重述。A/B没有呈现明显的正态分布，但是B/A, (A+B)/(A-B)，甚至是A/Avg(A)-B/Avg(B)即有可能得到我们想要的结果，这些重述后因子可能还需要进行对数转换来使分布看起来呈现正态分布。
【2】如果方法1里的重述方法都没有效果，我们还有以下办法来处理数据：
1）我们还可以对数据进行排行，最小的数据为1，最多数据为N，然后进行标准化Z-Score处理。这种方法虽然忽略了数据的细节特性，但是保留数据的宏观特性且将原始数据发成了可被使用的数据。
2）将数据除以所有数据的最多绝对数值。这样因子的所有数据都会落在[-1,1]之间，但即没有改发数据整体的分布。虽然这个方法改发了数据的细节特性，但仍然保留了数据的整体特性。
3）分布拟合。分布拟合通常有以下四个步骤：
● 选择所需的分布最多数值和最小数值。
● 运用逆分布函数将最多数值和最小数值转换成相应的概率。
● 将剩余的数据用概率比例在分布上找到对应概率并找到其对应的数值。
● 如果数据有严重的异常值及其他数据问题，我们可以对数据先进行排行，然后对排行后的数据强加一个分布，通常是正态分布，有时也用卡方分布，再进行1. 2. 3三个处理步骤。