日期统计
小蓝现在有一个长度为 100 的数组,数组中的每个元素的值都在 0 到 9 的范围之内。
数组中的元素从左至右如下所示:5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2
7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1
0 0 9 4 8 0 9 1 2 8 5 0 2 5 3 3
现在他想要从这个数组中寻找一些满足以下条件的子序列:
1. 子序列的长度为 8;
2. 这个子序列可以按照下标顺序组成一个 yyyymmdd 格式的日期,并且
要求这个日期是 2023 年中的某一天的日期,例如 20230902,20231223。
yyyy 表示年份,mm 表示月份,dd 表示天数,当月份或者天数的长度只有一位时需要一个前导零补充。
请你帮小蓝计算下按上述条件一共能找到多少个不同的 2023 年的日期。
对于相同的日期你只需要统计一次即可。
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
#include<bits/stdc++.h>
using namespace std;int ans;//合法日期的总数
bool vis[20240000];//记录这个合法日期或是错误日期是否出现过 ,初始化为0,若为1则直接返回falseint a[100];//记录输入的数组
bool check(int date){//检车这个日期是否是合法的日期
if(vis[date])return false;//之前出现过这个日期
vis[date]=1;//若是没出现过,则把该日期标记为1
//判断这个日期是否为合法的日期
int mm=date/100%100;//取日期的月份
int dd=date%100;//日期天数
if(mm<1||mm>12)return false;//如过月数不是1~12,返回false
if(mm==1||mm==3||mm==7||mm==8||mm==10||mm==12){//1,2,5,7,8,10,(腊)12三十一天不差,判断月份为这些时,日期是否在1~31,若果是则然会true
if(dd>=1&&dd<=31)return true;
}else if(mm==2){//2023年为闰年,所以有28天,判断月份为2时,日期是否在1~28,如果是则返回true,year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)判断闰年
if(dd<1||dd>28)
return true;
}else if(dd>=1&&mm<=30){//取余月份天数为20天,看是否为1~30,如果是则返回true
return true;
}else{
return false;//其余情况则返回false
}
}
void dfs(int x,int pos,int date){//x为输入数组当前下标的位置,pos为构成日期的位数一共8位,每一位都要满足特定的要求,date为当前时间的值,只有当pos为8位并且初步合法时,date才为完全值
if(x==100)return;//输入的数组遍历完,直接结束dfs
if(pos==8){//pos等于8时,则意味着日期的长度符合
if(check(date))++ans;//长度符合,check检查一下这个日期是否是合法日期,如果合法,则ans数量+1
return;
}
if((pos==0&&a[x]==2)||//日期的每一位都初步符合,如果日期的位数与其该位数上的数字是否符合它的限制,因为dfs是一位一位的递增,因此只能初步筛选日期每一位上的数字,只有等日期长度等于8时,才能完全判断这个日期是否合法
(pos==1&&a[x]==0)||
(pos==2&&a[x]==2)||
(pos==3&&a[x]==3)||
(pos==4&&0<=a[x]&&a[x]<=1)||
(pos==5&&0<=a[x]&&a[x]<=9)||
(pos==6&&0<=a[x]&&a[x]<=3)||
(pos==7&&0<=a[x]&&a[x]<=9))
dfs(x+1,pos+1,date*10+a[x]);//输入数组上的位置往后走,这一位合法pos往下走一位,临时的日期值*10+当前的这一位数字
dfs(x+1,pos,date);//输入数组位置往后走,这一位不合法,pos不+1,date也不改变
}
int main(){
ios::sync_with_stdio(0); cin.tie(0);//在C++中关闭输入输出流的同步,以提高程序的执行效率//cout.tie(0)
for(int i=0;i<100;i++)cin>>a[i]; //输入
dfs(0,0,0);//从第一个字符开始dfs
cout<<ans;//输出
return 0;
}
#include<bits/stdc++.h>
using namespace std;int ans;//合法日期的总数bool vis[20240000];//记录这个合法日期或是错误日期是否出现过 ,初始化为0,若为1则直接返回false int a[100];//记录输入的数组 bool check(int date){//检车这个日期是否是合法的日期 if(vis[date])return false;//之前出现过这个日期vis[date]=1;//若是没出现过,则把该日期标记为1 //判断这个日期是否为合法的日期 int mm=date/100%100;//取日期的月份 int dd=date%100;//日期天数 if(mm<1||mm>12)return false;//如过月数不是1~12,返回false if(mm==1||mm==3||mm==7||mm==8||mm==10||mm==12){//1,2,5,7,8,10,(腊)12三十一天不差,判断月份为这些时,日期是否在1~31,若果是则然会true if(dd>=1&&dd<=31)return true;}else if(mm==2){//2023年为闰年,所以有28天,判断月份为2时,日期是否在1~28,如果是则返回true if(dd<1||dd>28)return true;}else if(dd>=1&&mm<=30){//取余月份天数为20天,看是否为1~30,如果是则返回true return true;}else{return false;//其余情况则返回false }}void dfs(int x,int pos,int date){//x为输入数组当前下标的位置,pos为构成日期的位数一共8位,每一位都要满足特定的要求,date为当前时间的值,只有当pos为8位并且初步合法时,date才为完全值 if(x==100)return;//输入的数组遍历完,直接结束dfs if(pos==8){//pos等于8时,则意味着日期的长度符合 if(check(date))++ans;//长度符合,check检查一下这个日期是否是合法日期,如果合法,则ans数量+1 return;}if((pos==0&&a[x]==2)||//日期的每一位都初步符合,如果日期的位数与其该位数上的数字是否符合它的限制,因为dfs是一位一位的递增,因此只能初步筛选日期每一位上的数字,只有等日期长度等于8时,才能完全判断这个日期是否合法 (pos==1&&a[x]==0)||(pos==2&&a[x]==2)||(pos==3&&a[x]==3)||(pos==4&&0<=a[x]&&a[x]<=1)||(pos==5&&0<=a[x]&&a[x]<=9)||(pos==6&&0<=a[x]&&a[x]<=3)||(pos==7&&0<=a[x]&&a[x]<=9))dfs(x+1,pos+1,date*10+a[x]);//输入数组上的位置往后走,这一位合法pos往下走一位,临时的日期值*10+当前的这一位数字 dfs(x+1,pos,date);//输入数组位置往后走,这一位不合法,pos不+1,date也不改变
}
int main(){ios::sync_with_stdio(0); cin.tie(0);//在C++中关闭输入输出流的同步,以提高程序的执行效率//cout.tie(0) for(int i=0;i<100;i++)cin>>a[i]; //输入 dfs(0,0,0);//从第一个字符开始dfs cout<<ans;//输出 return 0;
} 01熵
对于一个长度为 n 的 01 串 S = x1x2x3...xn.
香农信息熵的定义为:
其中 p(0), p(1) 表示在这个 01 串中 0 和 1 出现的占比。
比如,对于S = 100 来说,信息熵 H(S ) = - 1/3 log2(1/3) - 2/3 log2(2/3) - 2/3 log2(2/3) = 1.3083。
对于一个长度为23333333 的 01 串,如果其信息熵为 11625907.5798,且 0 出现次数比 1 少,那么这个01 串中 0 出现了多少次?
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
#include<bits/stdc++.h>
using namespace std;
typedef long double db;
const int N=23333333;//01串的长度
const db ans=11625907.5798,eps=1e-4;//eps为误差10^-4,保持在这个误差范围内即可
//因为浮点型有有效位,所以肯定有一定误差
int main(){
//整体采用直接暴力的解法
for(int v=0;v<=N/2;++v){//v为0的个数,因为0的个数是小于1的,因此小于总数的一半
int u=N-v;//u为1的个数
db res=-1.0*u*u/N*log2(1.0*u/N)-1.0*v*v/N*log2(1.0*v/N);//log2()函数求log以2为底的对数
if(fabs(res-ans)<eps){//两者相减去绝对值小于误差,则符合条件 fabs函数求绝对值
cout<<v;//输出0的个数
return 0;
}
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
typedef long double db;
const int N=23333333;//01串的长度
const db ans=11625907.5798,eps=1e-4;//eps为误差10^-4,保持在这个误差范围内即可
//因为浮点型有有效位,所以肯定有一定误差
int main(){//整体采用直接暴力的解法 for(int v=0;v<=N/2;++v){//v为0的个数,因为0的个数是小于1的,因此小于总数的一半 int u=N-v;//u为1的个数 db res=-1.0*u*u/N*log2(1.0*u/N)-1.0*v*v/N*log2(1.0*v/N);//log2()函数求log以2为底的对数 if(fabs(res-ans)<eps){//两者相减去绝对值小于误差,则符合条件 fabs函数求绝对值 cout<<v;//输出0的个数 return 0;}}return 0;
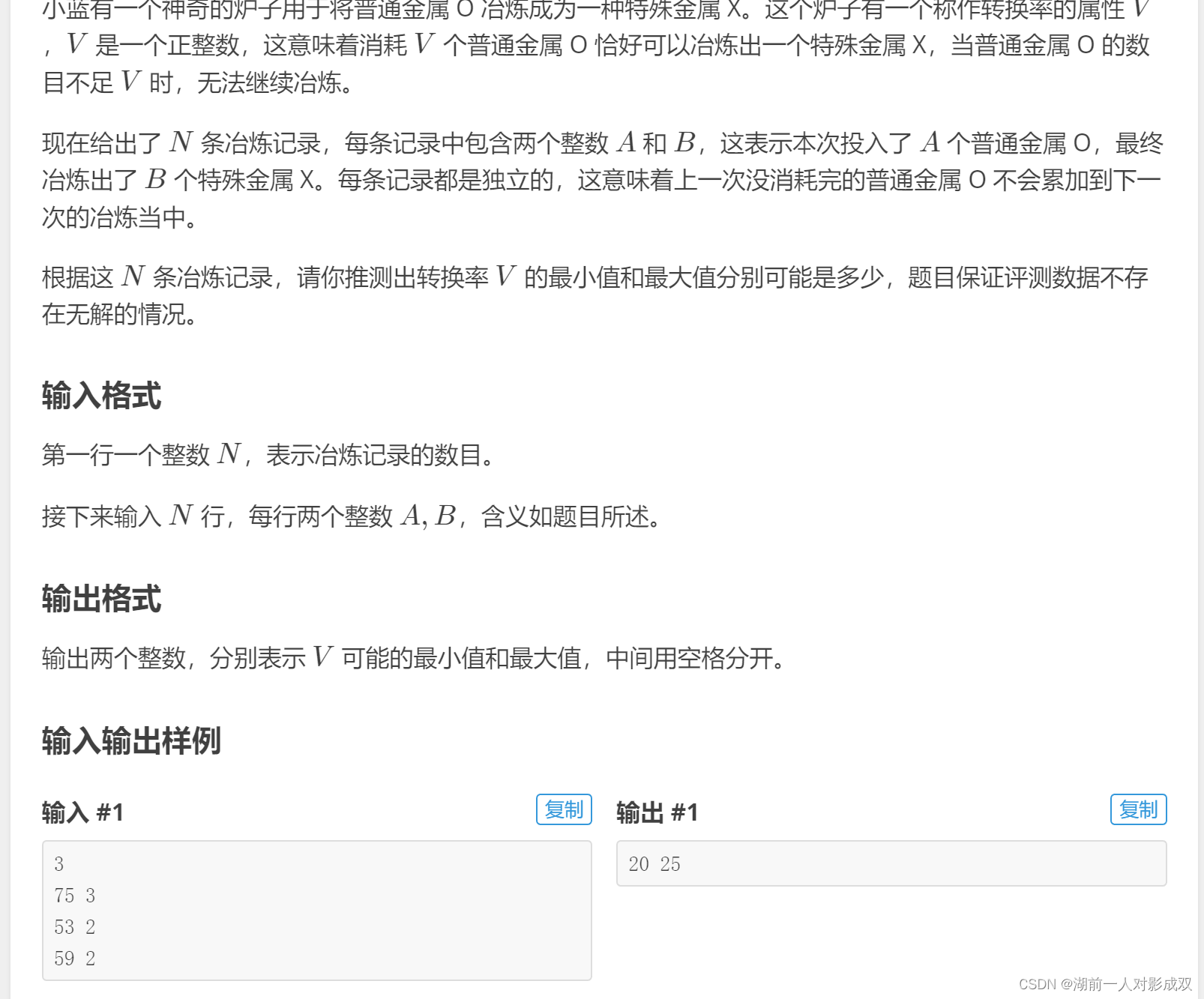
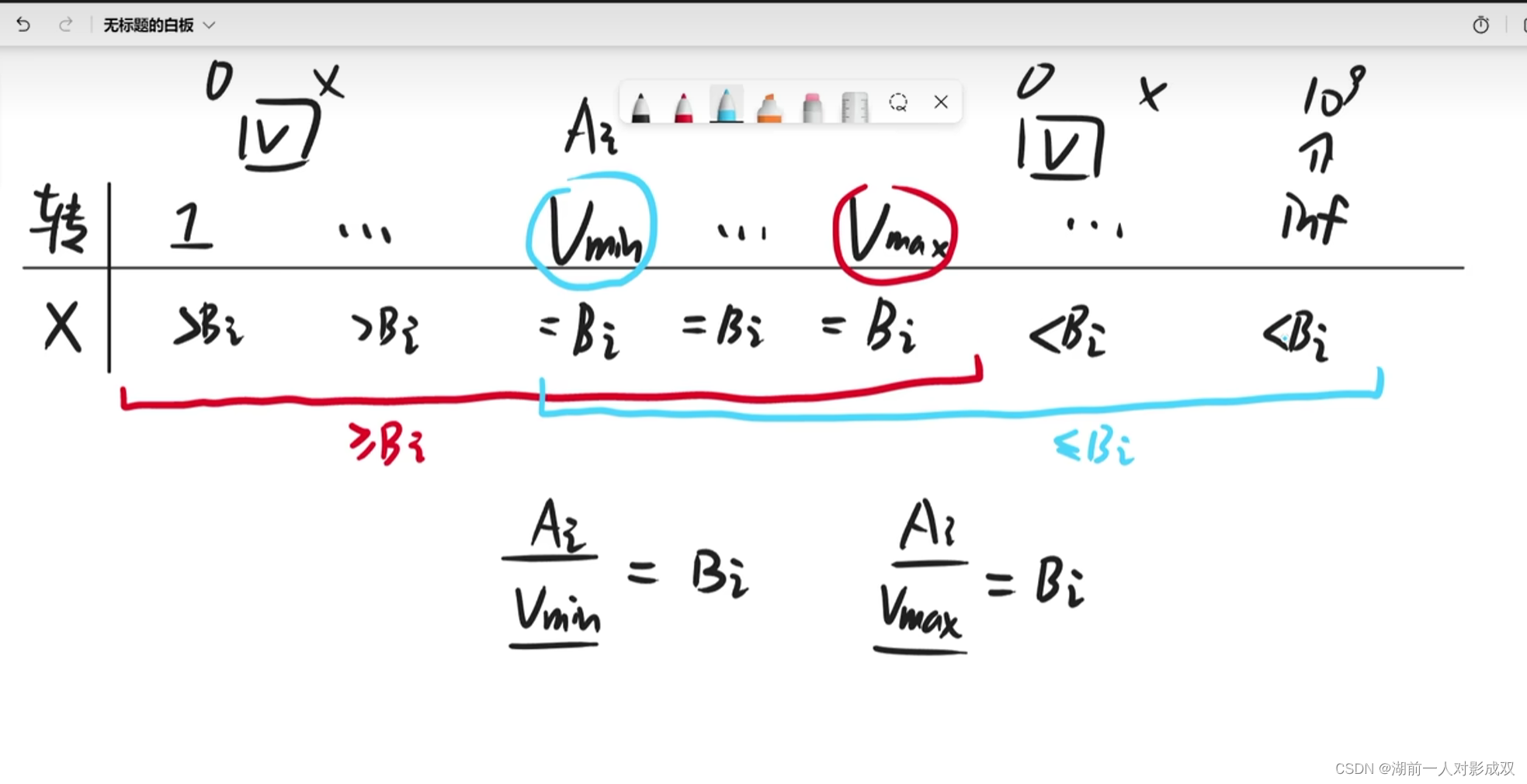
} 冶炼金属

#include<bits/stdc++.h>
using namespace std;
const int MAX_N=1e4+1;
int N,A[MAX_N],B[MAX_N];
bool check_min(int v){for(int i=1;i<=N;i++){if(A[i]/v>B[i])return false;return true; }
}bool check_max( int v){for(int i=1;i<=N;i++){if(A[i]/V<B[i])return false;return true;}
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cin>>N;for(int i=0;i<=N;i++){cin>>A[i]>>B[i];}int L=1,R=1000000000,V_min;while(l<R){int mid=L+R>>1;if(check_min(mid)){V_min=mid;R=mid-1; }else{L=mid+1;}}int L=1,R=1000000000,V_max;while(l<R){int mid=L+R>>1;if(check_max(mid)){V_max=mid;L=mid+1; }else{R=mid-1;}}cout<<v_min<<" "<<v_max;return 0;
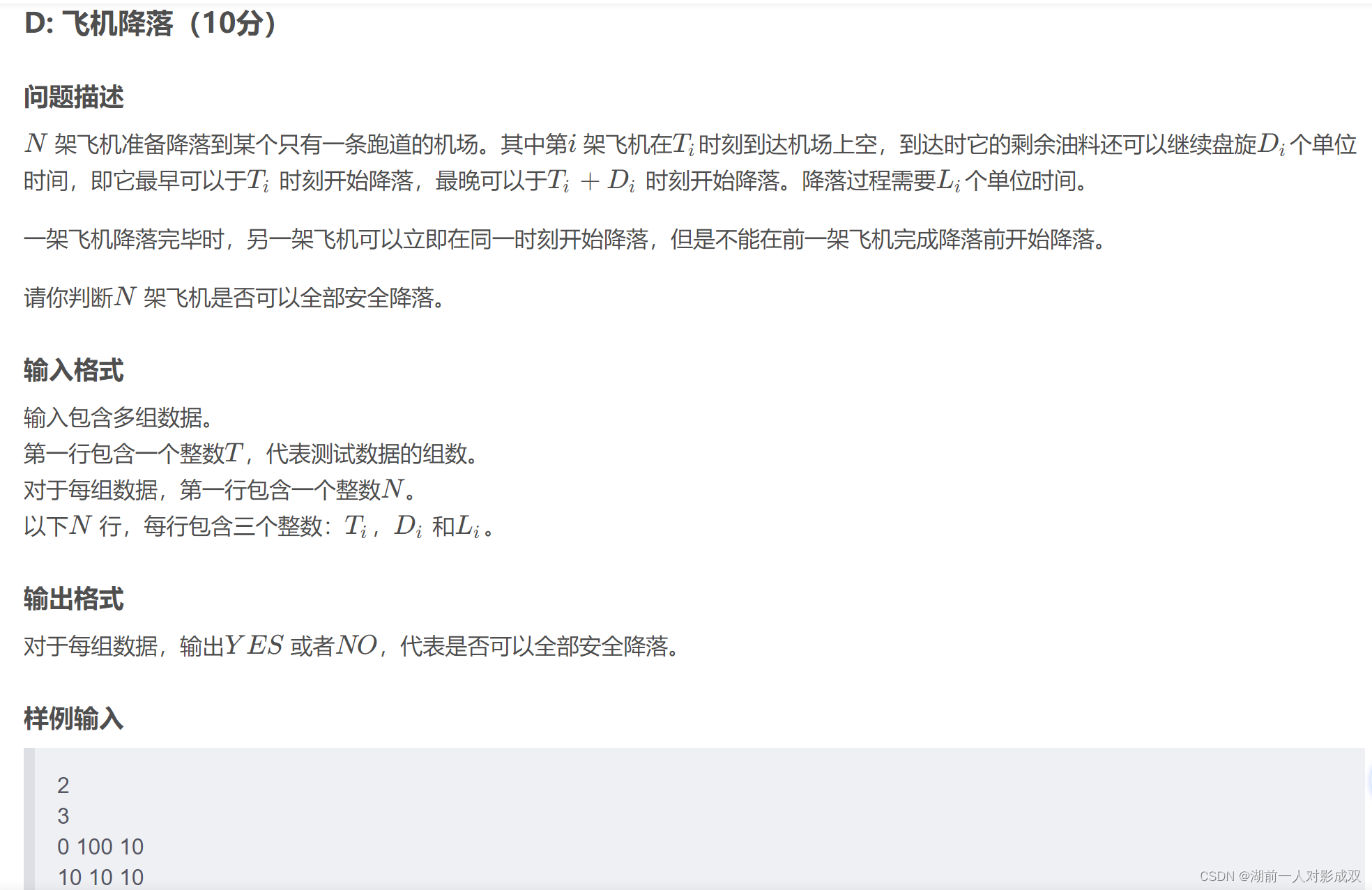
}飞机降落
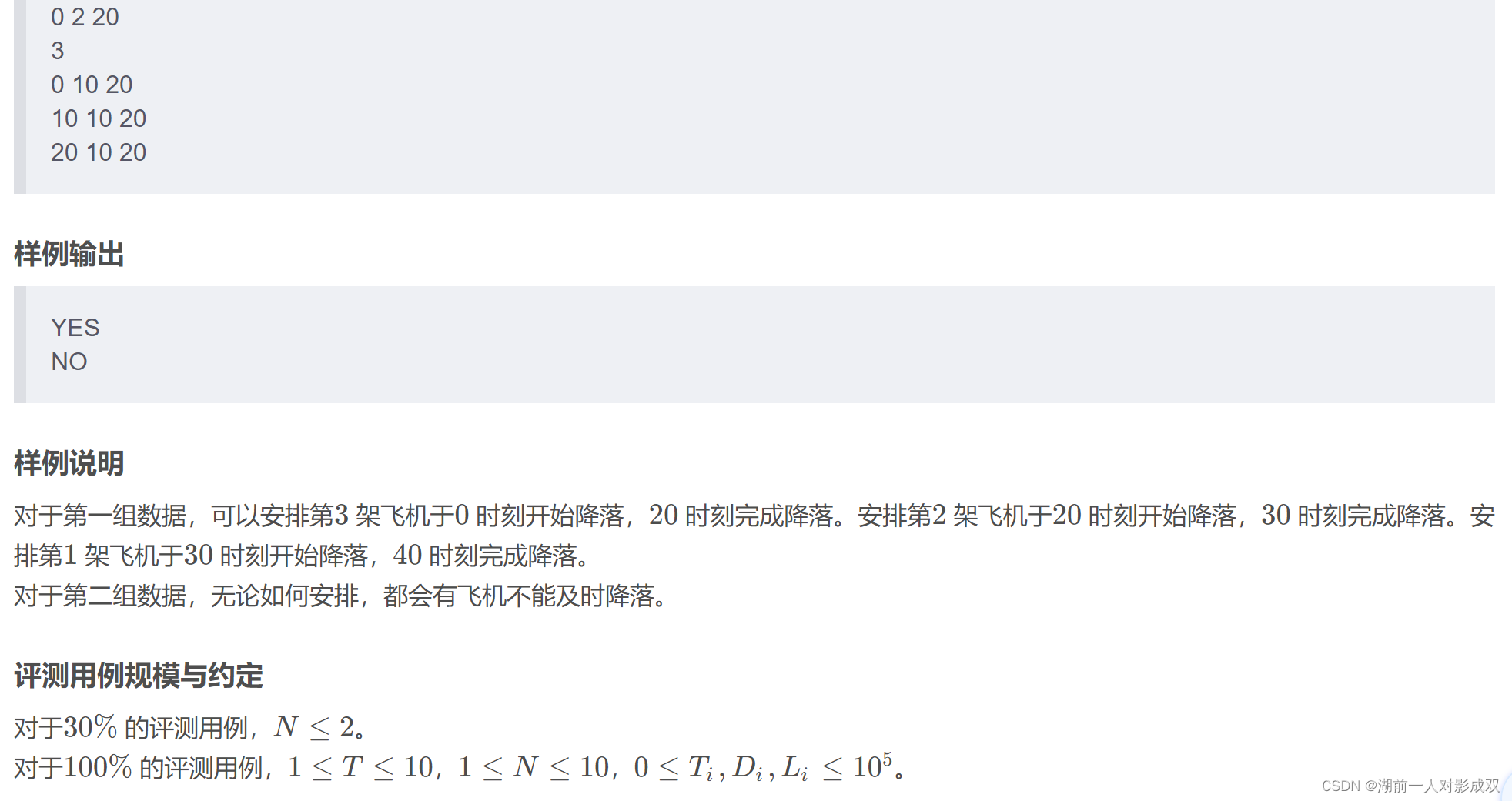
#include<bits/stdc++.h>
using namespace std;
const int MAX_N=11;
int n;
int N,T[MAX_N],D[MAX_N],L[MAX_N];bool used[MAX_N],have_answer;
void dfs(int x,int tim){if(have_answer)return;if(x==n){have_answer=1;return;}for(int i=1;i<=n;i++){if(!used[i]&&tim<=T[i]+D[i])used[i]=1;dfs(x+1,max(tim,T[i])+D[i]);if(have_answer)return;used[i]=0;}
}
void solve(){cin>>N;for(int i=1;i<=N;i++){cin>>T[i]>>D[i]>>L[i];used[i]=0;}dfs(0,0);if(have_answer)cout<<"YES\n";else cout<<"NO\n";}int main(){ios::sync_with_stdio(0);cin.tie(0);int T;cin>>T;while(T--)solve();return 0;
}接龙数列
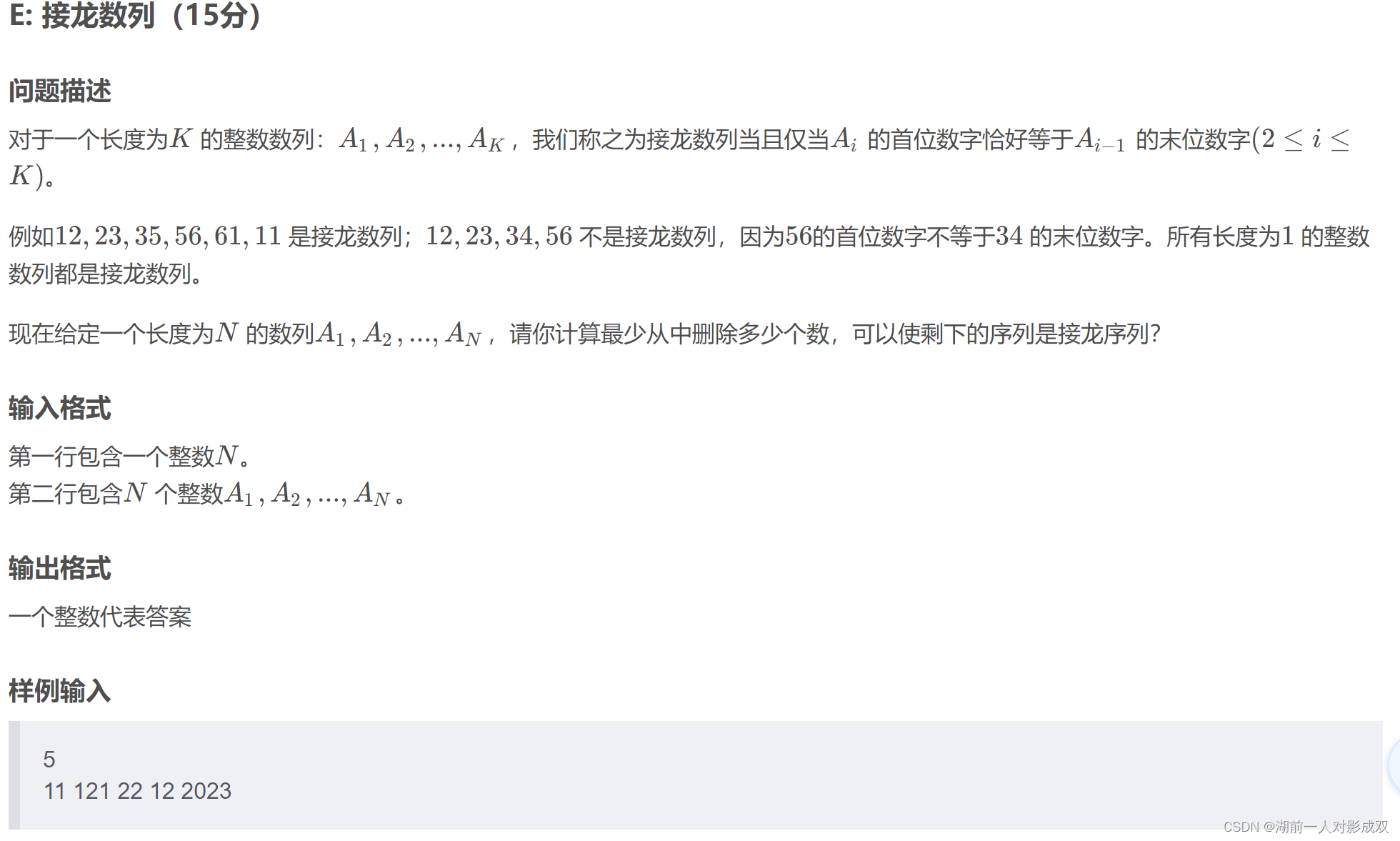
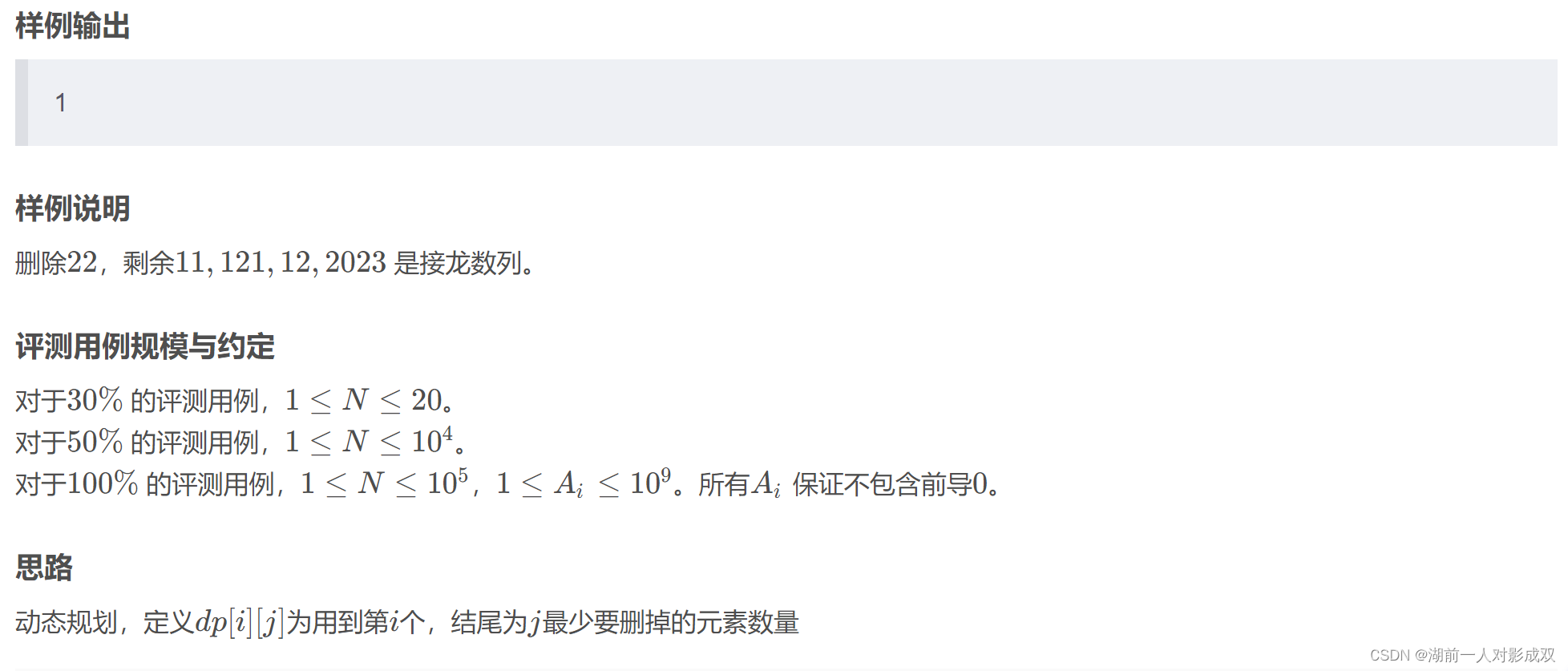
#include<bits/stdc++.h>
using namespace std;
const int MAX_N=1e5+5;
int N,dp[10];int main(){ios::sync_with_stdio(0);cin.tie(0);cin>>N;for(int i=0;i<=N;i++){int A;cin>>A;vector<int>d;while(A){d.push_back(A%10);A/10;} int y=*d.begin(),x=d.back();dp[y]=max(dp[y],dp[x]+1); }int len=0;for(int i=0;i<10;i++){len=max(len,dp[i]);}cout<<N-len;return 0;
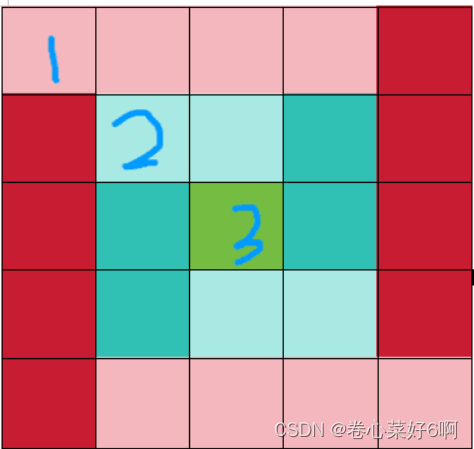
}岛屿数量

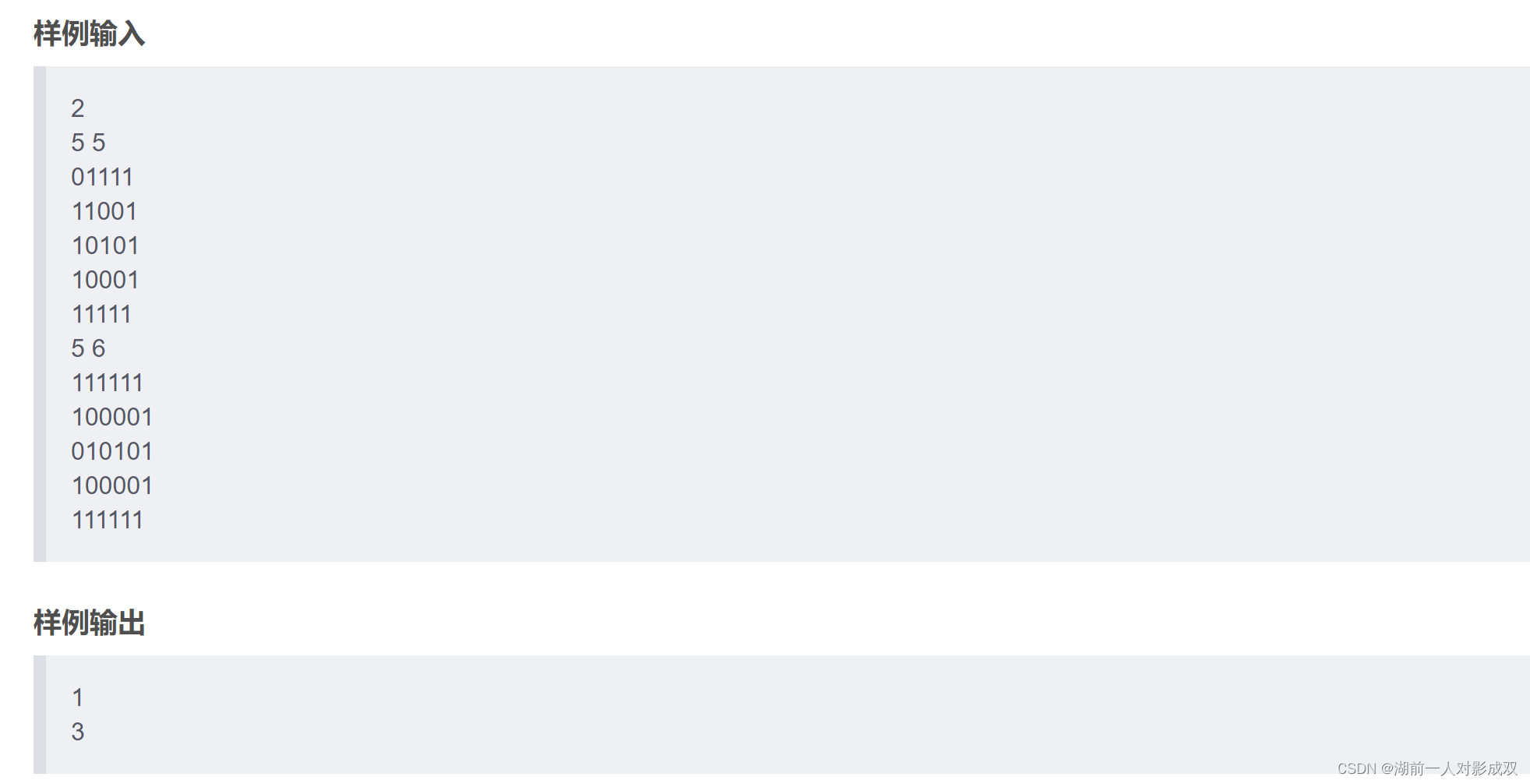

#include<bits/stdc++.h>
using namespace std;
const int MAX_N=51;
int M,N;
string mp[MAX_N];
bool vis[MAX_N][MAX_N];//对岛进行染色
bool used[MAX_N][MAX_N];//是否逃出去,没检查一个岛,都要进行标记,因为当下一次遍历到该岛,
int dx[]={0,0,1,-1,1,-1,1,-1};
int dy[]={1,-1,0,0,-1,1,1,-1};
void bfs_col(int x,int y){queue<int>qx,qy;qx.push(x);qy.push(y);vis[x][y]=1;//bfs坐标放进队列后,就标记 while(!qx.empty()){x=qx.front();qx.pop(); y=qy.front();qy.pop();for(int i=0;i<4;i++ ){int nx=x+dx[i];int ny=y+dy[i];if(nx<0||M<=nx||ny<0||N<=ny||vis[ny][nx]||mp[nx][ny]=='0')continue;//越界或是海水,或被访问过就跳过 qx.push(nx);qy.push(ny);vis[nx][ny]=1;//标记 } }
} bool bfs_out(int x,int y){//逃出去 for(int i=0;i<M;i++)for(int j=0;j<N;j++)used[i][j]=0;//清空标记,从0开始找出口 queue<int>qx,qy;qx.push(x);qy.push(y); used[x][y]=1;//放入队列后再标记,下一次不能再访问while(!qx.empty()){x=qx.front();qx.pop();y=qy.front();qy.pop(); if(x==0||x==M-1||y==0||y==N-1)return true;//如果到达边界(到达边界,而不是超越边界),就返回true; for(int i=0;i<8;i++){int nx=x+dx[i];int ny=y+dy[i];if(nx<0||M<=nx||ny<0||N<=ny||used[ny][nx]||mp[nx][ny]=='1')continue;qx.push(nx);qy.push(ny);used[nx][ny]=1;//标记的目的是为了让他不走回头路 }}}void solve(){cin>>M>>N;for(int i=0;i<M;i++){cin>>mp[i];for(int j=0;j<N;j++){vis[i][j]=0; }} int ans=0;for(int i=0;i<M;i++){for(int j=0;j<N;j++){if(!vis[i][j]&&mp[i][j]=='1'){bfs_out(i,j);//先进行染色 if(bfs_out(i,j))++ans;//看是否能逃出去,若是该点为内岛,则外岛已经被染色 }}}cout<<ans<<'\n'; }int main(){ios::sync_with_stdio(0);cin.tie(0);int T;cin>>T;while(T--){solve();}return 0;
} 
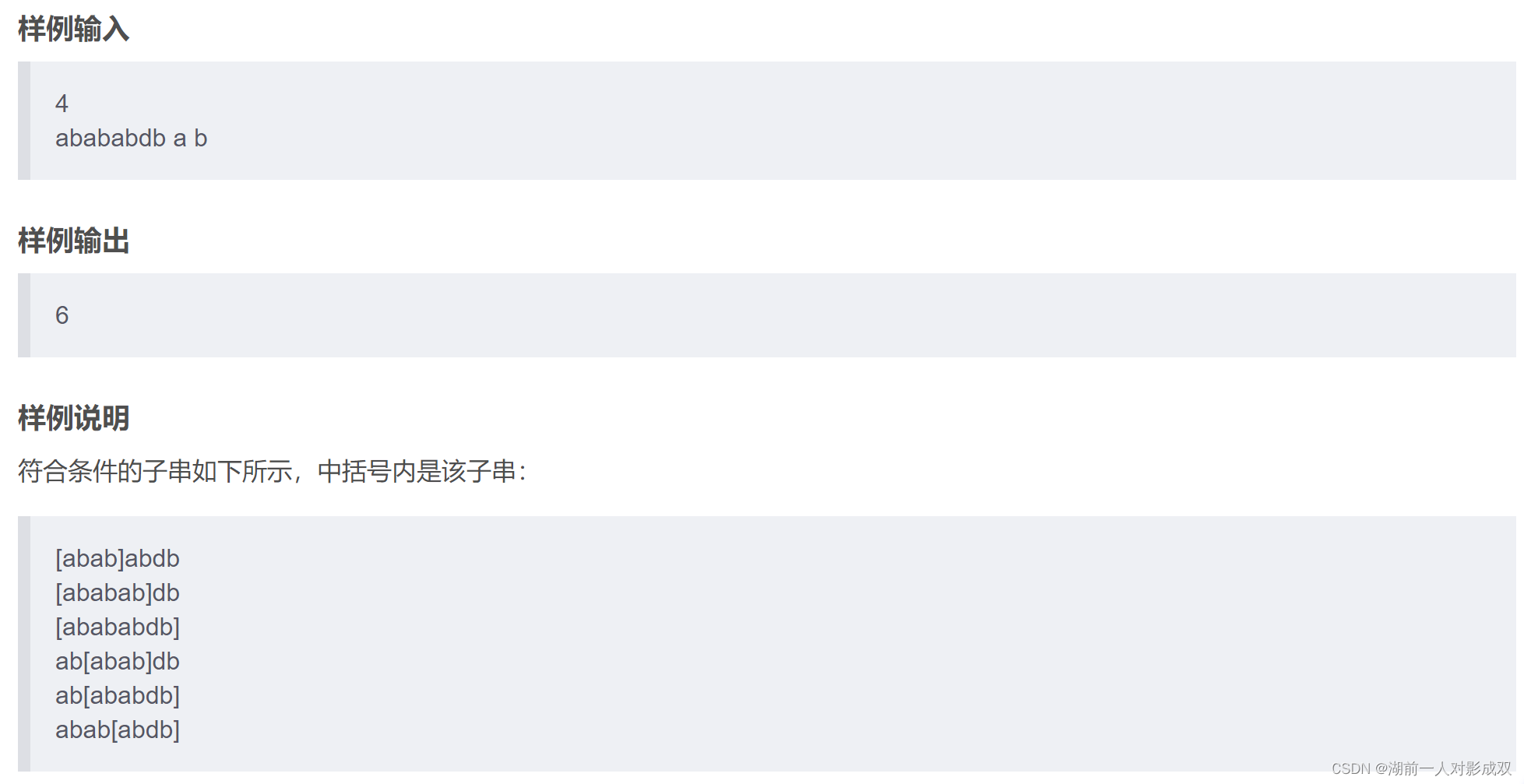

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int K;
string S;
char c1,c2;
int main(){cin>>K>>S>>c1>>c2;int sum_c1=0;int n=S.size();for(int i=k-1,j=0;i<n;i++,j++){//前缀和,sum_c1记录前面a的数量,当i所在位置为b时,子串简写的数量就是b前面a的数量,不包括前k个位置内的a, if(S[j]==c1)++sum_c1;if(S[i]==c2)ans+=sum_c1;}cout<<ans;return 0;return 0;
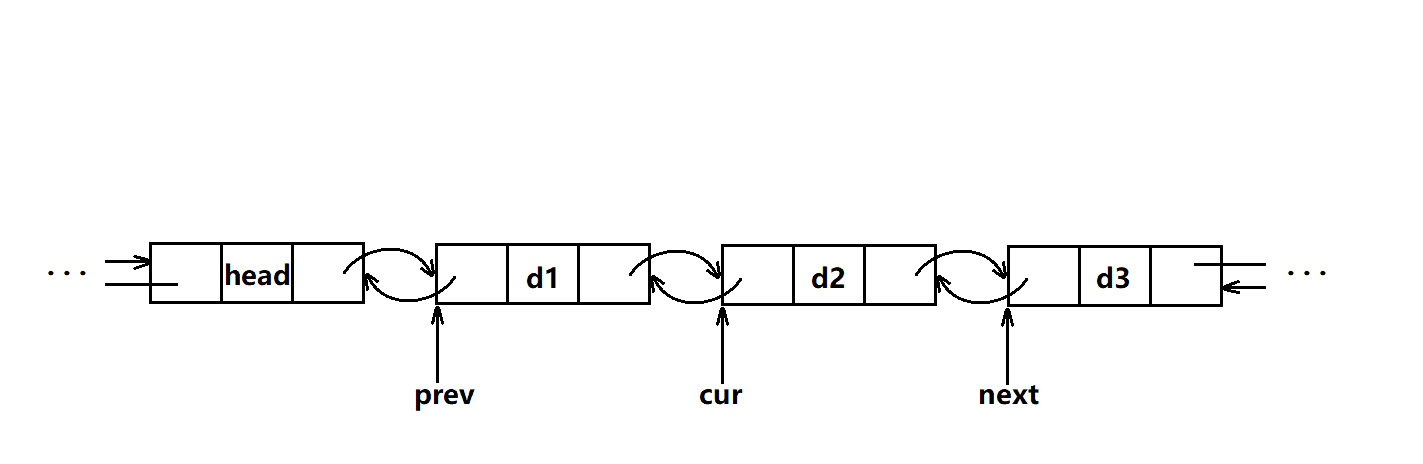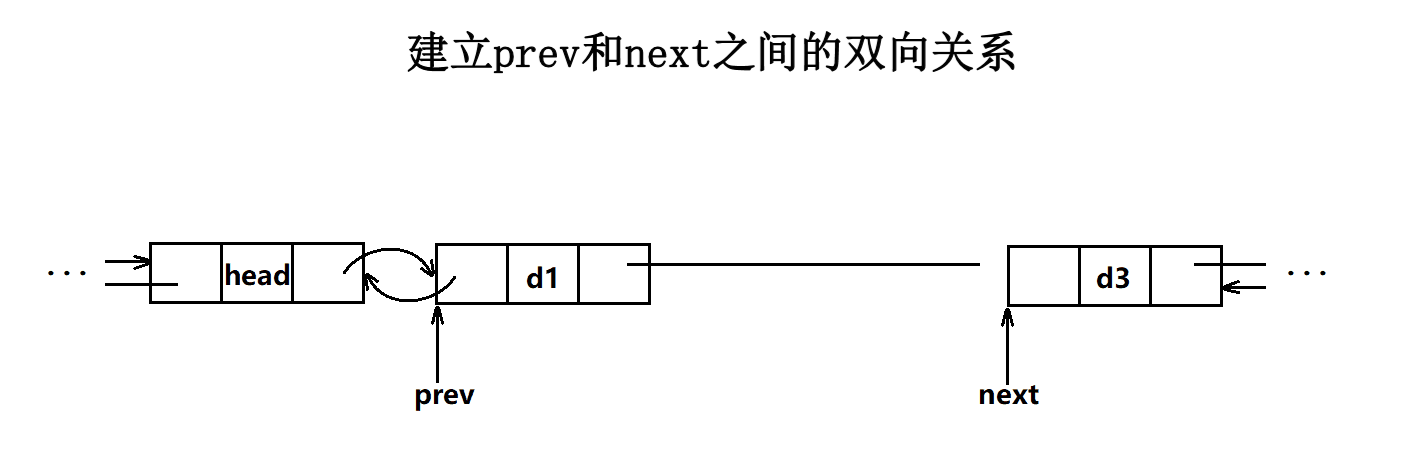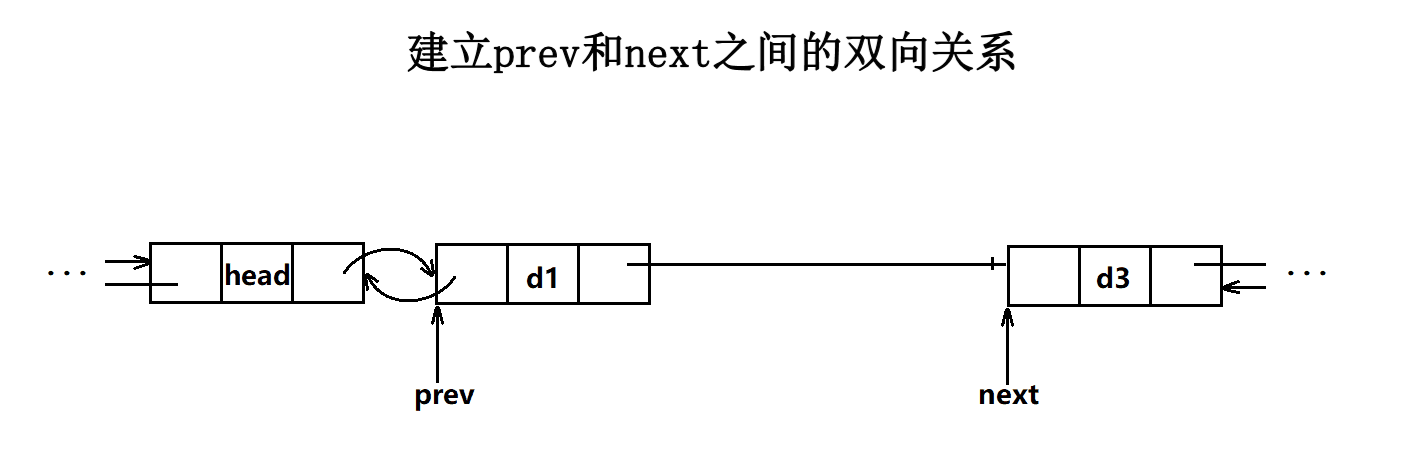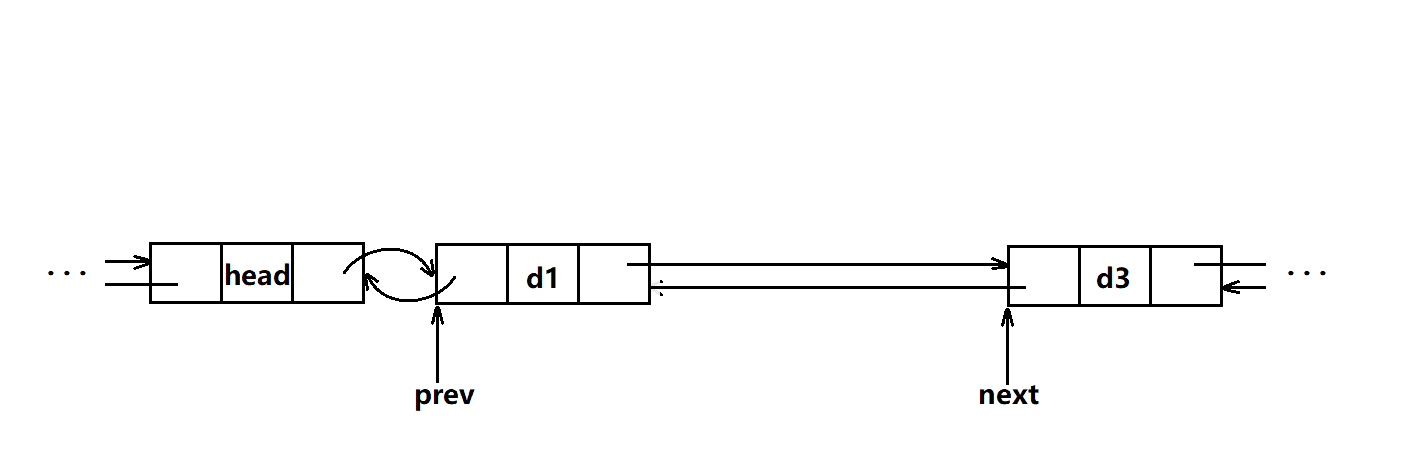
}整数删除
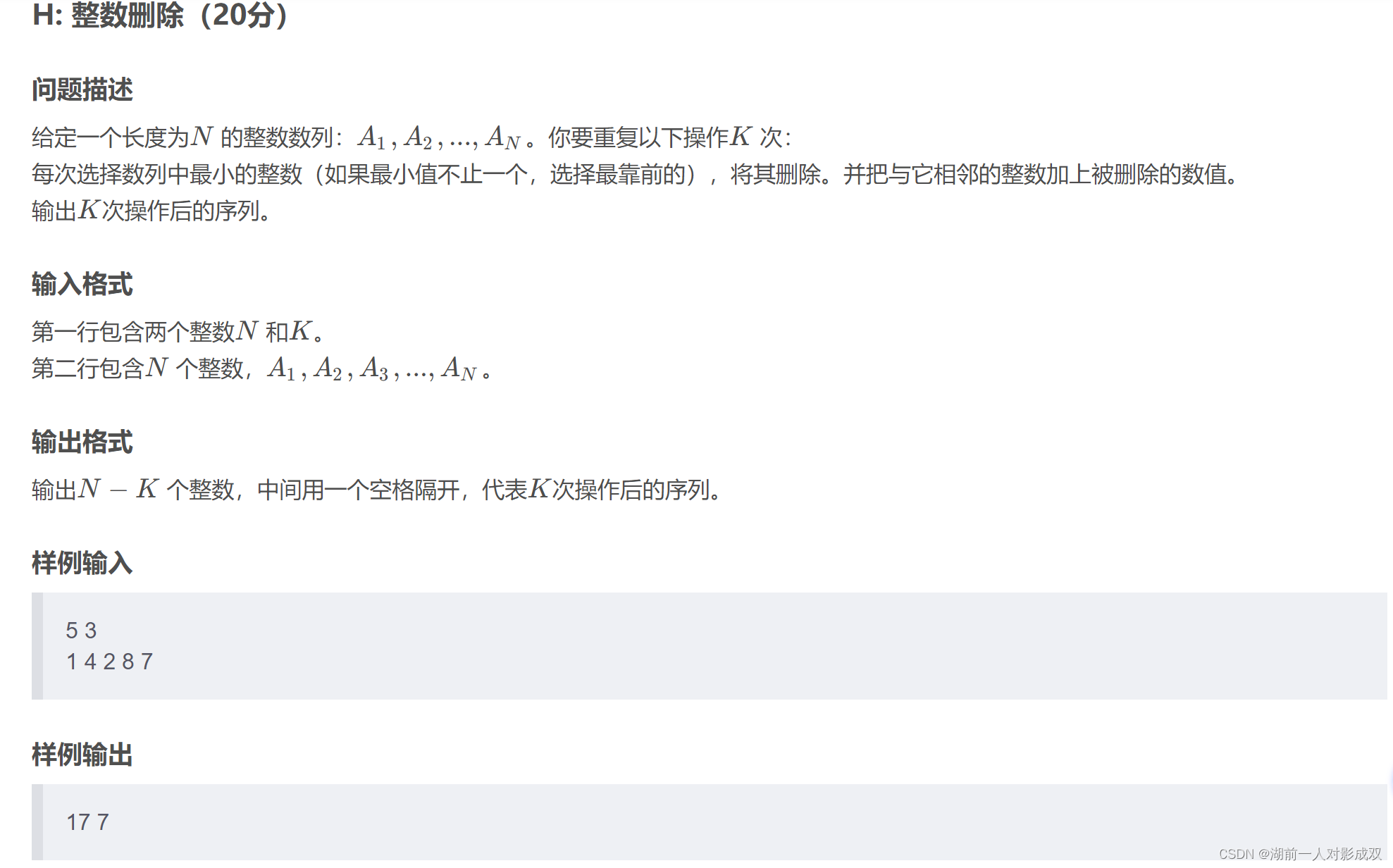

#include<bits/stdc++.h>
using namespace std;
#define val first
#define pos second
const int MAX_N=5e5+5;
int N,K,pre[MAX_N],nxt[MAX_N];
typedef long long LL;
typedef pair<LL,int>PLI;
priority_queue<PLI>q;
LL A[MAX_N]; int main(){ios::sync_with_stdio(0);cin.tie(0);cin>>N>>K;for(int i=1;i<=N;i++){cin>>A[i];pre[i]=i-1;nxt[i]=i+1;q.push({-A[i],-i});}pre[1]=-1;nxt[N]=-1;while(K--){PLI now;do{now=q.top();q.pop();now.val=-now.val;now.pos=-now.pos;//原本是负的,该为正的 }while(A[now.pos]!=now.val);int PRE=pre[now.pos];int NXT=nxt[now.pos];if(PRE!=-1){A[PRE]+=now.val;q.push({-A[PRE],-PRE});nxt[PRE]=NXT;}if(NXT!=-1){A[NXT]+=now.val;q.push({-A[NXT],-NXT});pre[NXT]=PRE;}A[now.pos]=-1;}for(int i=1;i<=N;i++){if(A[i]!=-1){cout<<A[i]<<' ';}}return 0;
}景区导游

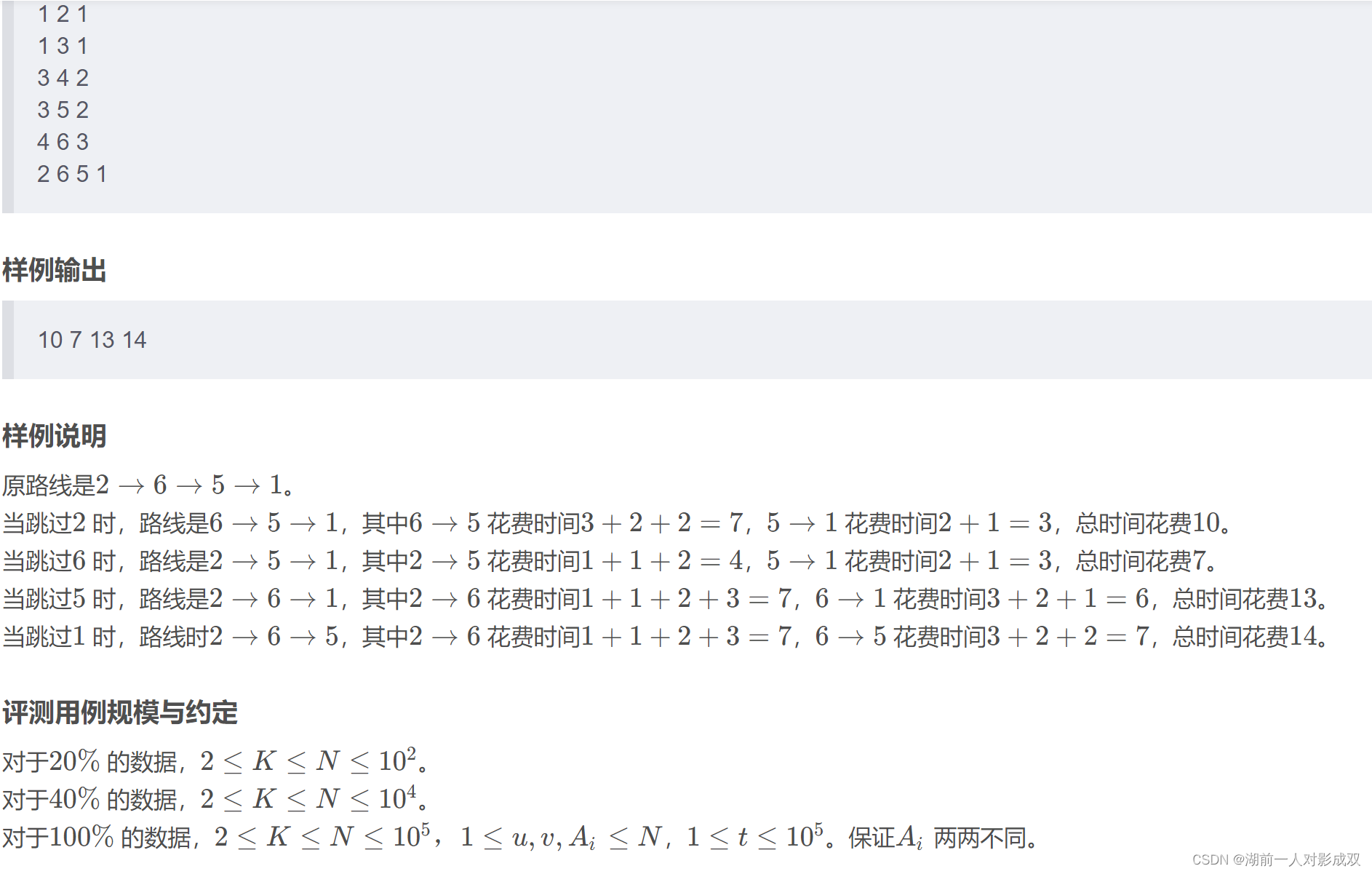
DFS遍历图(暴力做法)
正解:树上前缀和、最近公共祖先树:一种数据结构,无环连通图
无环连通图-->任意两个点之间存在唯一的一条路径
2 6 5 1
记作一个点都不去掉之前,总的花费记作sum
(1)去掉2 sum-cost[2->6]
(2)去掉6 sum-cost[2->6]-cost[6->5]+cost[2->5]
(3)去掉5 sum-cost[6->5]-cost[5->1]+cost[6->1]
(4)去掉1 sum-cost[5->1]暴力做法:DFS:O(n)
优化后的做法,树上前缀和+最近公共祖先O(logn)
图的存储:
链式前向型:链表
vector容器存图
二者的原理: 存储当前点的邻接点
x->y
edge[x].push_back(y);存储了一条x->y的边
无向边的存储,就是存储两条有向边
x-y
edge[x].push_back(y);
edge[y].push_back(x);DFS组成{
iF()
{ 递归终止的条件
}
往下递归的过程
}
#include<bits/stdc++.h>
#define endl '\n'
#define deb(x) cout<<ax<<" = "<<x<<'\n';
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int N=2e5+10;
typedef pair<int,int> pii;
map<pil,int>st;//记录从x到y的距离是多少
int a[N];
vector<pii>edge[N];//存图 //dfs的参数不是一下就想到的,而是在写的1过程中发
//现你需要某个信息,而这个信息你没有提前记录 ,
//那么你可以把这个信息当作一个参数,此时就达到了记录信息的目的 //s路程的起点
//v路径的终点
//u你当前走到了哪个点
//father当前这个点的父亲节点是谁,避免重复走
//sum从s走到u的路径花费总和
bool dfs(int s,int u,int father,int v,int sum){if(u==v){st[{s,v}]=sum;st[{v,s}]=sum;return true; } for(int i=0;i<edge[u].size();i++){int son=edge[u][i].first;if(son==father){continue;}int w=edge[u][i].second;if(dfs(s,son,u,v,sum+w))//如果找到了,直接return true即可,剩下的不用遍历; return true;}return false;}void solve(){int n,k;cin>>n>>k;for(int i=0;i<n;i++){int x,y,t;cin>>x>>y>>t;edge[x].push_back({y,t});//存图 edge[y].push_back({x,t});}for(int i=0;i<k;++){//存路线 cin>>a[i];} int ans=0;for(int i=0;i<k-1;i++){dfs(a[i],a[i],-1,a[i+1],0);//路线上的点位之间的距离 ans+=st[{a[i],a[i+1]}];}for(int i=0;i<k;i++){int tmp=ans;/*记作一个点都不去掉之前,总的花费记作sum
(1)去掉2 sum-cost[2->6]
(2)去掉6 sum-cost[2->6]-cost[6->5]+cost[2->5]
(3)去掉5 sum-cost[6->5]-cost[5->1]+cost[6->1]
(4)去掉1 sum-cost[5->1]
*/if(i==0){tmp-=st[{a[i],a[i+1]}];}else if(i==k-1){tmp-=st[{a[i-1],a[i]}];}else{tmp-=st[{a[i-1],a[i]}];tmp-=st[{a[i],a[i+1]}];dfs(a[i-1],a[i+1],-1,a[i+1],0);tmp+=st[{a[i-1],a[i+1]}];}cout<<tmp<<endl;}}
上面复杂度优点高了
正解是优化cost的求法
可以在O(n)的复杂度内预处理出来当前带你到根节点的距离
6->5的距离=cost[0->1]+cost[5->1]-2*cost[3->1]
求最近的公共祖先
3是6和5的最近公共祖先公共祖先求解的过程是logn
最近公共祖先:
一共有三种写法,倍增,树链部分,tarjan
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAX_N=1e5+1;
vector<int>E[MAX_N],W[MAX_N];
int N,K,dep[MAX_N],fa[MAX_N][21],A[MAX_N];
LL dis[MAX_N];//用倍增法求最近公共父节点
void dfs(int u,int Fa){dep[u]=dep[Fa]+1;fa[u][0]=Fa;for(int i=1;i<=20;i++){fa[u][i]=fa[fa[u][i-1]][i-1]; }for(int i=0;i<E[u].size();i++){int v=E[u][i],w=W[u][i];if(v==Fa)continue;dis[v]=dis[u]+w;dfs(v,u);}
}int LCA(int u,int v){if(dep[u]<dep[v])swap(u,v);for(int i=20;i>=0;i--){if(dep[fa[u][i]]>=dep[v])u=fa[u][i];}if(u==v)return u;for(int i=20;i>=0;i++){if(fa[u][i]!=fa[v][i]){u=fa[u][i];v=fa[v][i];}}return fa[u][0];}LL path_dis(int u,int v){if(!u||!v)return 0;//如果删除的点是两边的其中一边,在减该点没有边的点到它的距离时,则返回零 //涉及不存在的点时,返回0; return dis[u]+dis[v]-2*dis[LCA(u,v)];
}
int main() {ios::sync_with_stdio(0);cin.tie(0);cin>>N>>K;for(int i=1;i<N;++i){int u,v,t; cin>>u>>v>>t;E[u].push_back(v);W[u].push_back(t);E[v].push_back(u);W[v].push_back(t);} dfs(1,0);LL ans=0;for(int i=1;i<N;i++){cin>>A[i];ans+=path_dis(A[i],A[i-1]);//总长度 }for(int i=1;i<=k;i++){//减去两点到该点的距离,加上两点之间的距离 cout<<ans-path_dis(A[i-1],A[i])-path_dis(A[i],A[i+1])+path_dis(A[i-1],A[i+1])<<' ';}return 0;}砍树

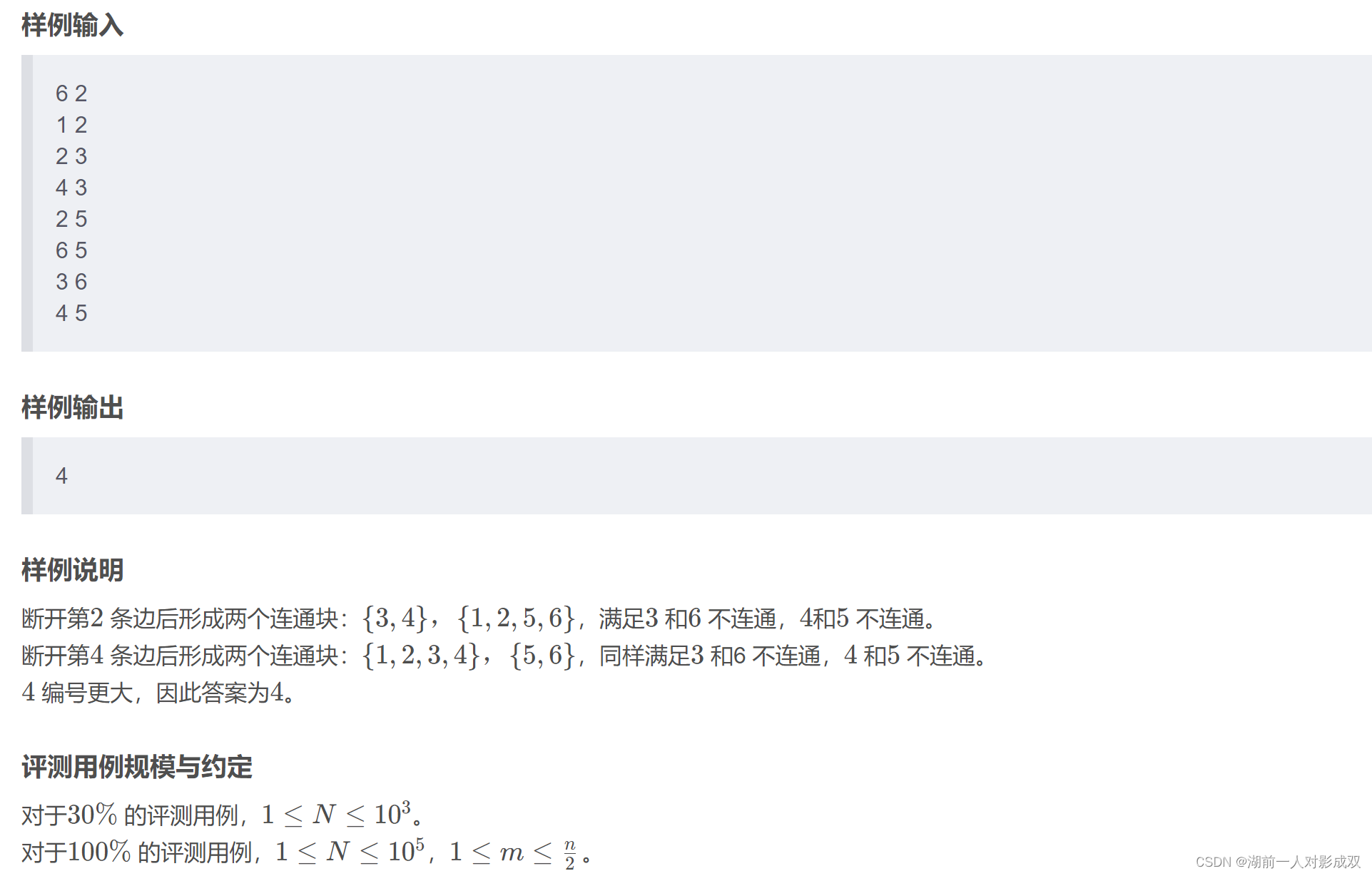
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
vector<int>e[N],num[N];
int n,m,dep[N],s[N],fa[N][21],ans; void dfs(int u,int Fa){dep[u]=dep[Fa]+1;fa[u][0]=Fa;for(int i=1;i<20;i++){fa[u][i]=fa[fa[u][i-1]][i-1];}for(auto &v:e[u]){//c11if(v==Fa)continue;dfs(v,u);}
}
void dfs2(int u,int Fa){for(int i=0;i<e[u].size();i++){int v=e[u][i],p=num[u][i];if(v==Fa)continue;dfs2(v,u);s[u]+=s[v];//差分 if(s[v]==m)ans==max(ans,p);}
}int LCA(int u,int v){if(dep[u]<dep[v])swap(u,v); for(int i=20;i>=0;i--){if(dep[fa[u][i]]>=dep[v])u=fa[u][i];}if(u==v)return u;for(int i=20;i>=0;i--){if(fa[u][i]!=fa[v][i]){u=fa[u][i];v=fa[v][i];} }return fa[u][0];
}int main(){cin>>n>>m;for(int i=1;i<n;i++){int x,y;cin>>x>>y;e[x].push_back(y);num[x].push_back(i);e[y].push_back(x);num[y].push_back(i);}dfs(1,0);for(int i=1;i<=m;i++){int a,b;cin>>a>>b;s[a]++;s[b]++;s[LCA(a,b)]-=2;
//两点到最近公共祖先那停止,若想断开两点,深度需要小于两点的最近公共祖先 即高于公共祖先的边,取消掉两点的差分和}dfs2(1,0);cout<<ans<<endl;return 0;
}