Python大数据分析——一元与多元线性回归模型
- 相关分析
- 概念
- 示例
- 一元线性回归模型
- 概念
- 理论分析
- 函数
- 示例
- 多元线性回归模型
- 概念
- 理论分析
- 示例
- 线性回归模型的假设检验
- 模型的F检验
- 理论分析
- 示例
- 模型的T检验
- 理论分析
- 示例
相关分析
概念
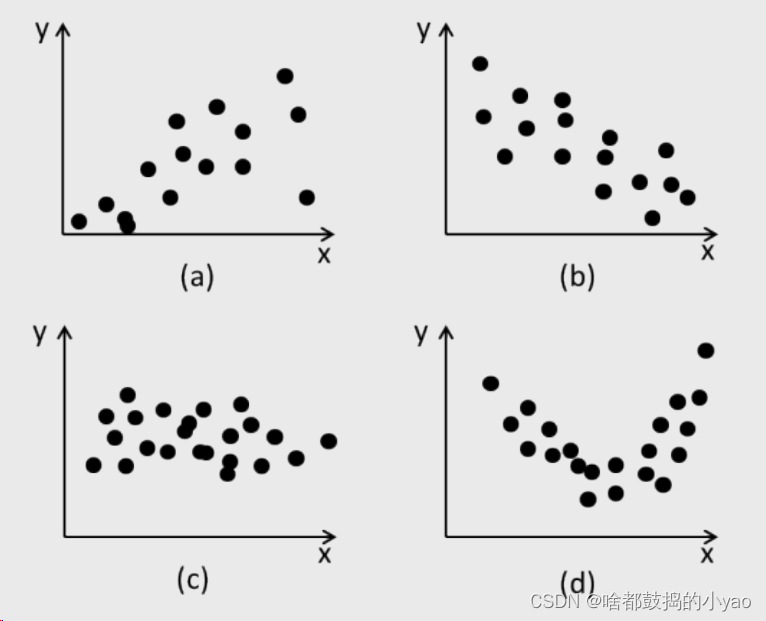
a 正相关;b 负相关;c 不相关;d 存在关系但不存在线性关系
相关系数的计算:

相关系数ρ一定是取[-1,1]之间的数
示例
对于一元的:
# 导入第三方模块
import pandas as pd
income = pd.read_csv('D:\pythonProject\data\Salary_Data.csv')
# 查看变量有哪些
income.columns
# 查看两者的相关性
income.Salary.corr(income.YearsExperience)
输出:
0.9782416184887598
对于多元的:
# 导入第三方模块
import pandas as pd
# 导入数据
Profit = pd.read_excel(r'D:\pythonProject\data\Predict to Profit.xlsx')
# 查看变量有哪些
Profit.columns
# 查看多对一的相关性(要删除其中的离散变量)
Profit.drop('State', axis=1).corrwith(Profit['Profit'])
输出:

如果在多元中找两两的相关性用:
# 导入第三方模块
import pandas as pd
# 导入数据
Profit = pd.read_excel(r'D:\pythonProject\data\Predict to Profit.xlsx')
# 查看变量有哪些
Profit.columns
# 查看两两的相关性(要删除其中的离散变量)
Profit.drop('State', axis=1).corr()
输出:
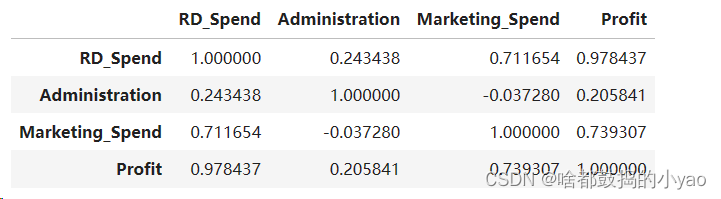
一元线性回归模型
概念
一元线性回归是分析只有一个自变量(自变量x和因变量y)线性相关关系的方法。一个经济指标的数值往往受许多因素影响,若其中只有一个因素是主要的,起决定性作用,则可用一元线性回归进行预测分析。
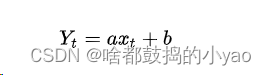
理论分析
首先观察点的分布
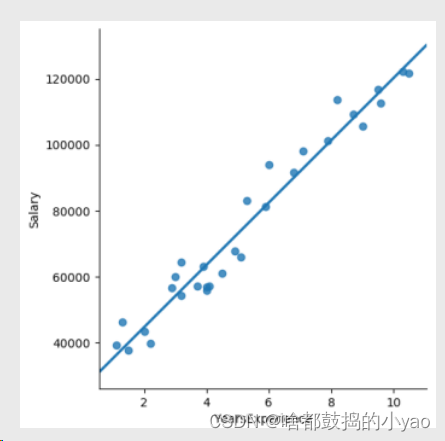
1、两边变量之间存在明显的线性关系;
2、根据常识,工作年限是因,薪资水平是果;
3、是否存在某个模型(即图中的一次函数)可以刻画两个变量
之间的关系呢?
可以根据一元线性函数可得
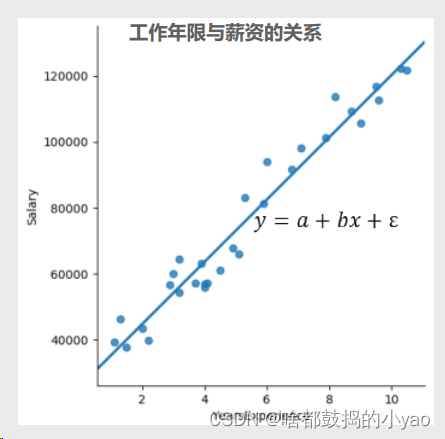
1、模型中的x称为自变量,y称为因变量;
2、a为模型的截距项,b为模型的斜率项,ε为模型的误差项;
3、误差项ε的存在主要是为了平衡等号两边的值,通常被称为模型
无法解释的部分;
那么接下来就要考虑a和b如何求解
为了确保生成的线与点的距离靠近,也就是距离最近。
思路:
1、如果拟合线能够精确地捕捉到每一个点(即所有散点全部落在拟
合线上),那么对应的误差项ε应该为0;
2、所以,模型拟合的越好,则误差项ε应该越小。进而可以理解为:
求解参数的问题便是求解误差平方和最小的问题;
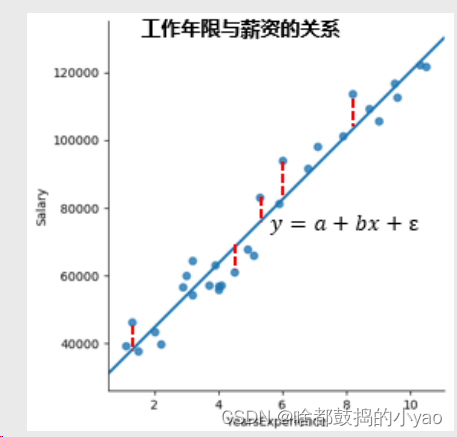
那么公式就为
为什么是平方,因为当点在生成线的下面时,差值为负,为了防止正负相消,我们取平方的值保障为正。
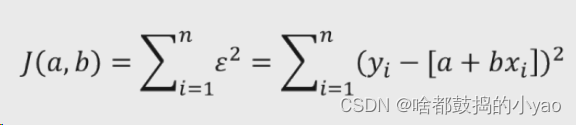
1、J(a,b)为目标函数,需求这个函数的最小值
2、我们求J最小值,求解方法便是计算目标函数关于参数a和b的两个偏导数,最终令偏导数为0即可。(因为当函数的导数=0的时候,函数取极值)
数学推导过程
1、展开目标函数中的平方项
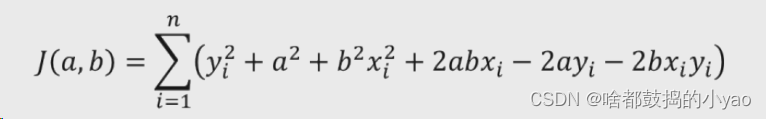
2、计算a和b的偏导数,并令其为0
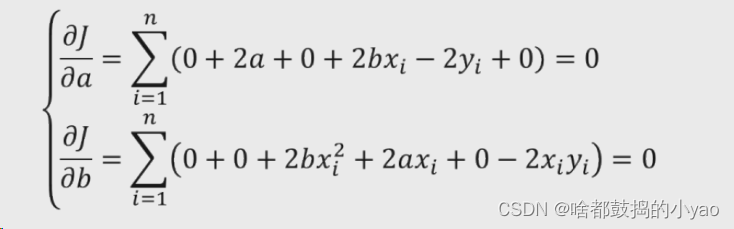
3、转换公式
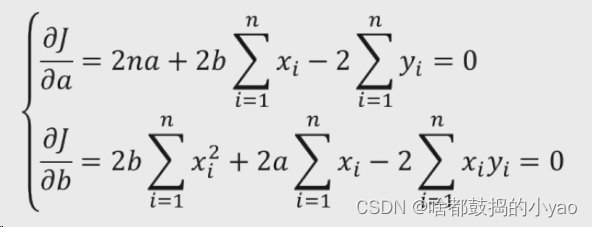
4、化简为a和b为0的形式
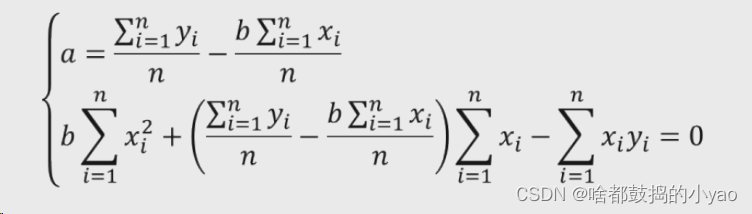
不难发现a的两个求和再除以n的计算为y和x的平均值,并再次化简a和b为
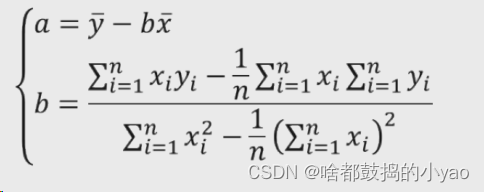
函数
#导入第三方模块
import statsmodels.api as sm
sm.ols(formula, data, subset=None, drop_cols=None)
formula:以字符串的形式指定线性回归模型的公式,如’y~x’就表示简单线性回归模型
data:指定建模的数据集
subset:通过bool类型的数组对象,获取data的子集用于建模
drop_cols:指定需要从data中删除的变量
其中ols,我们指的是最小二乘法
示例
# 导入第三方模块
import pandas as pd
import statsmodels.api as sm
income = pd.read_csv('D:\pythonProject\data\Salary_Data.csv')
# 利用收入数据集,构建回归模型
fit = sm.formula.ols('Salary ~ YearsExperience', data = income).fit()
# 返回模型的参数值
fit.params
输出:

a也就是Intercept,截距
b也就是YearsExperience,斜率
多元线性回归模型
概念
对于一元线性回归模型来说,其反映的是单个自变量对因变量的影响,然而实际情况中,影响因变量的自变量往往不止一个,从而需要将一元线性回归模型扩展到多元线性回归模型。
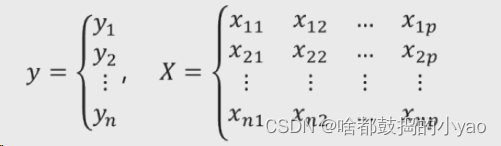
其中,xij 代表第 i 行的第 j 变量值。如果按照一元线性回归模型的逻辑,那么多元线性回归模型应该就是因变量y与自变量X的线性组合。
所以,基于一元线性回归模型的扩展,可以将多元线性回归模型表示为:
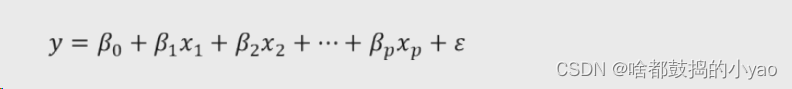
进一步,根据线性代数的知识,可以将上式表示为矩阵的形式:

理论分析
首先构造目标函数(跟一元思路一样)
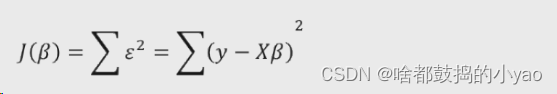
展开平方项
在线性代数里,Σz^2=z’*z(z’为z的转置)
为了方便理解举个例子:
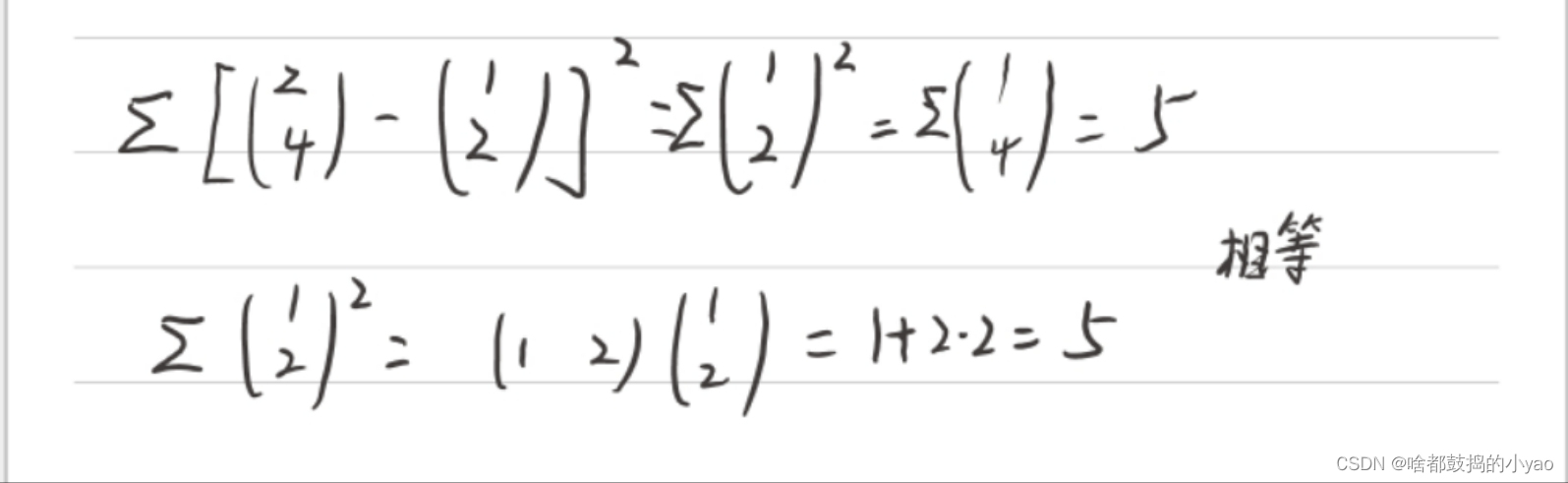
那么我们就可得
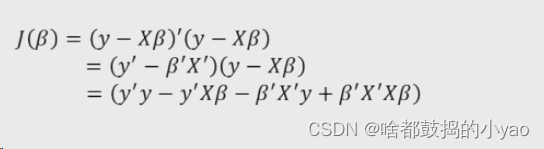
求偏导为0
这里要补充点矩阵求导知识点

更多矩阵求导内容请点击这里
根据上面计算,由此我们可得
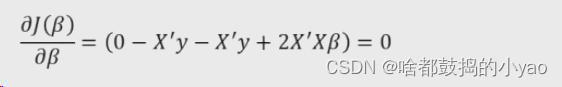
计算偏回归函数
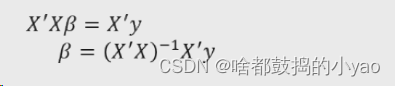
示例
数据内容为
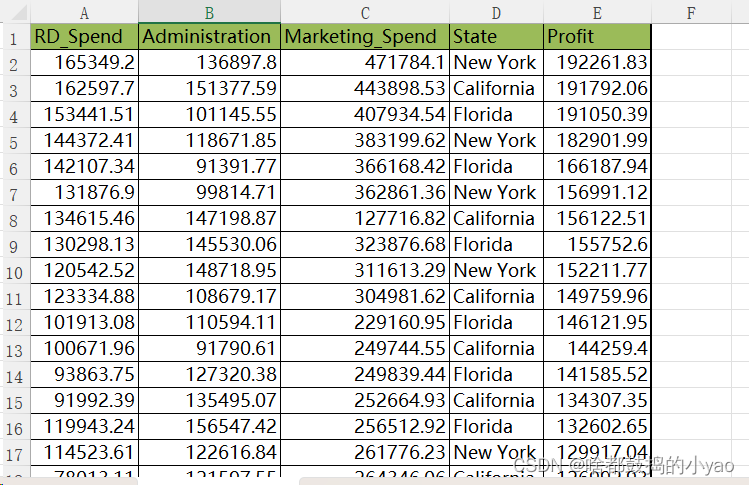
数据集包含5个变量,分别是产品的研发成本、管理成本、市场营销成本、销售市场和销售利润。
# 导入第三方模块
import pandas as pd
import statsmodels.api as sm
from sklearn import model_selection
# 导入数据
Profit = pd.read_excel(r'D:\pythonProject\data\Predict to Profit.xlsx')
# 将数据集拆分为训练集和测试集,测试集为20%
train, test = model_selection.train_test_split(Profit, test_size = 0.2, random_state=1234)
# 根据train数据集建模,默认为连续的数学变量,而State变成了分类变量
model = sm.formula.ols('Profit ~ RD_Spend+Administration+Marketing_Spend+C(State)', data = train).fit()
print('模型的偏回归系数分别为:\n', model.params)
# 删除test数据集中的Profit变量,用剩下的自变量进行预测
test_X = test.drop(labels = 'Profit', axis = 1)
pred = model.predict(exog = test_X)
print('对比预测值和实际值的差异:\n',pd.DataFrame({'Prediction':pred,'Real':test.Profit}))
输出:
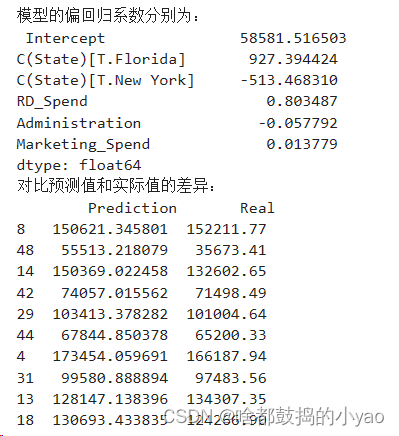
Intercept 为截距;其余的为系数变量
在预测与实际值比较,差异小说明拟合好,差异大说明不好
注意!
x变量要是全是连续变量p,那么输出的变量也是一致的,也是p
但若出现字符串,那么我们想要字符串也变成数字变量,我们就需要改成分类变量,也就是x2_1, x2_2等,在这里面就是New York和Florida,拆分成了两个x2,那为什么不是全部的?因为在分类变量里,二者会出现强相关内部关系,p会大,不满足线性回归的假设前提,我们需要抛去一个(不过程序会默认砍掉一个)
那么当然我们也可以自己选择删除的变量
默认情况下,对于离散变量State而言,模型选择California值作为对照组。
# 导入第三方模块
import pandas as pd
import statsmodels.api as sm
from sklearn import model_selection
# 导入数据
Profit = pd.read_excel(r'D:\pythonProject\data\Predict to Profit.xlsx')
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit,dummies], axis = 1)
# 删除State变量和California变量(因为State变量已被分解为哑变量,New York变量需要作为参照组)
Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)
# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+Florida+California', data = train).fit()
print('模型的偏回归系数分别为:\n', model2.params)
输出:
我们可以看到没了纽约,而有了其他的
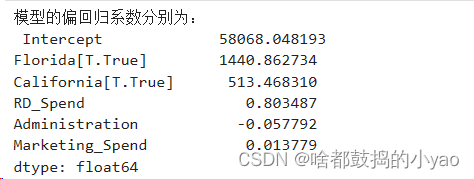
那最后函数可写成:Profit=58068.05+0.80RDSpend-0.06Administation+0.01Marketing_Spend+1440.86Florida
+513.47California
线性回归模型的假设检验
做假设检验的目的,是看我们构造的模型合不合理。
模型的F检验
F检验是检验模型的合理性
1、提出问题的原假设和备择假设
2、在原假设的条件下,构造统计量F
3、根据样本信息,计算统计量的值
4、对比统计量的值和理论F分布的值,当统计量值超过理论值时,拒绝原假设,否则接受原假设
理论分析
首先构造假设
H0叫原假设;H1叫备择假设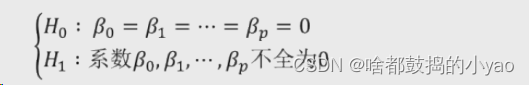
再构造统计量

n是变量数目,p是样本数目
计算的F与分布的理论F(p, n-p-1)两者相互比对
其中:
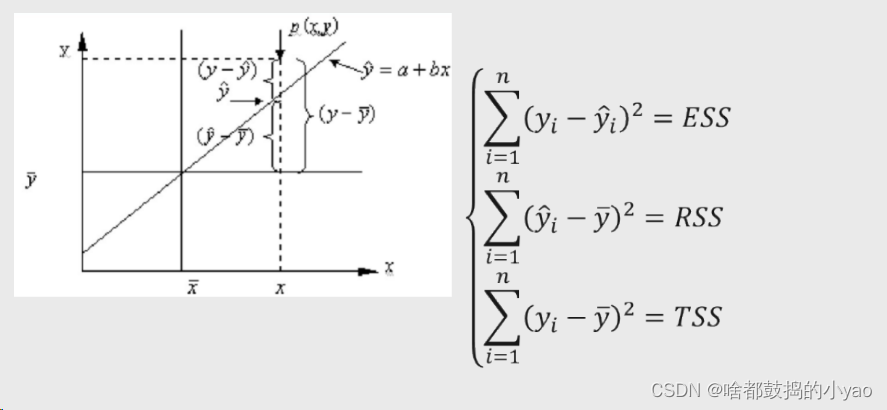
TSS=ESS+RSS
ESS叫离差/残差平方和
RSS叫回归平方和
TSS叫总差平方和
示例
我们先建模,然后做F检验
# 导入第三方模块
import pandas as pd
import statsmodels.api as sm
from sklearn import model_selection
# 导入数据
Profit = pd.read_excel(r'D:\pythonProject\data\Predict to Profit.xlsx')
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit,dummies], axis = 1)
# 删除State变量和California变量(因为State变量已被分解为哑变量,New York变量需要作为参照组)
Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)
# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+Florida+California', data = train).fit()
# print('模型的偏回归系数分别为:\n', model2.params)# 导入第三方模块
import numpy as np
# 计算建模数据中因变量的均值
ybar = train.Profit.mean()
# 统计变量个数和观测个数
p = model2.df_model
n = train.shape[0]
# 计算回归离差平方和
RSS = np.sum((model2.fittedvalues-ybar) ** 2)
# 计算误差平方和
ESS = np.sum(model2.resid ** 2)
# 计算F统计量的值
F = (RSS/p)/(ESS/(n-p-1))
print('F统计量的值:',F)
输出:
F统计量的值: 174.63721716733755
接着对比实际
# 导入模块
from scipy.stats import f
# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
print('F分布的理论值为:',F_Theroy)
输出:
F分布的理论值为: 2.502635007415366
我们发现,计算出来的F统计量值174.64远远大于F分布的理论值2.50,所以应当拒绝原假设,即认为多元线性回归模型是显著的,也就是说回归模型的偏回归系数都不全为0。
模型的T检验
T检验是检验系数的合理性
理论分析
首先提出假设

构造统计量

ε是误差项;cjj是(X’X)^-1的对角线,也就是(X’X)逆的对角线
示例
利用model的方法
# 导入第三方模块
import pandas as pd
import statsmodels.api as sm
from sklearn import model_selection
# 导入数据
Profit = pd.read_excel(r'D:\pythonProject\data\Predict to Profit.xlsx')
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit,dummies], axis = 1)
# 删除State变量和California变量(因为State变量已被分解为哑变量,New York变量需要作为参照组)
Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)
# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+Florida+California', data = train).fit()
# print('模型的偏回归系数分别为:\n', model2.params)# 有关模型的概览信息
model2.summary()
输出:
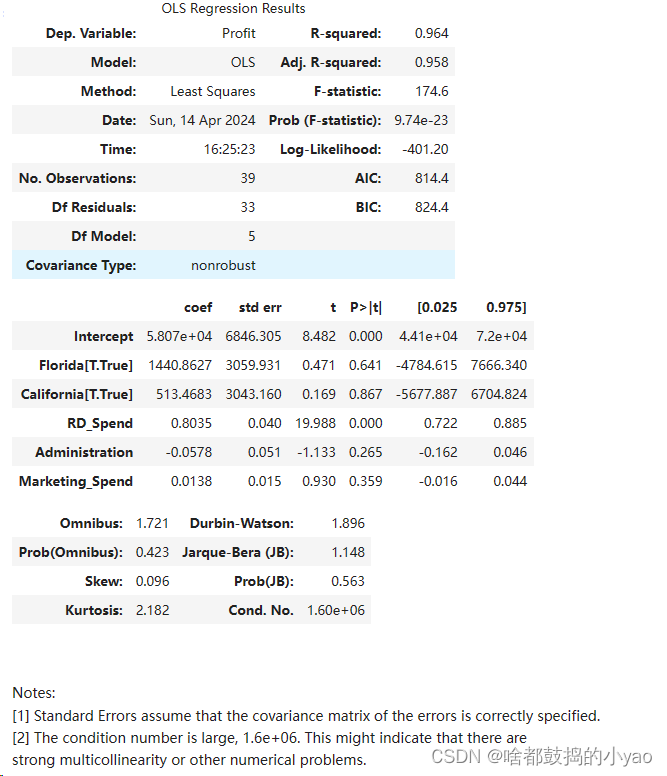
对比下结论
p≤0.05时才通过,或者叫t的绝对值大于2
从返回的结果可知,只有截距项Intercept和研发成本RD Spend对应的p值小于0.05,其余变量都没有通过系数的显著性检验,即在模型中这些变量不是影响利润的重要因素。