用c++实现串匹配问题、选择排序

5.2.2 串匹配问题

【问题】 给定两个字符串S和T，在主串S中查找子串T的过程称为串匹配(string matching,也称模式匹配），T称为模式。在文本处理系统、操作系统、编译系统、数据库系统以及 Internet 信息检索系统中，串匹配是使用最频繁的操作。串匹配问题具有两个明显的特征：①问题规模很大，常常需要在大量信息中进行匹配，因此，算法的一次执行时间不容忽视；②匹配操作执行频率高，因此，算法改进所取得的效益因积累往往比表面上看起来要大得多。

应用实例 在 Word等文本编辑器中有这样一个功能：在“查找”对话框中输入待查找内容（常见的是查找某个字或词），编辑器会在整个文档中进行查找，将与待查找内容相匹配的部分高亮显示，
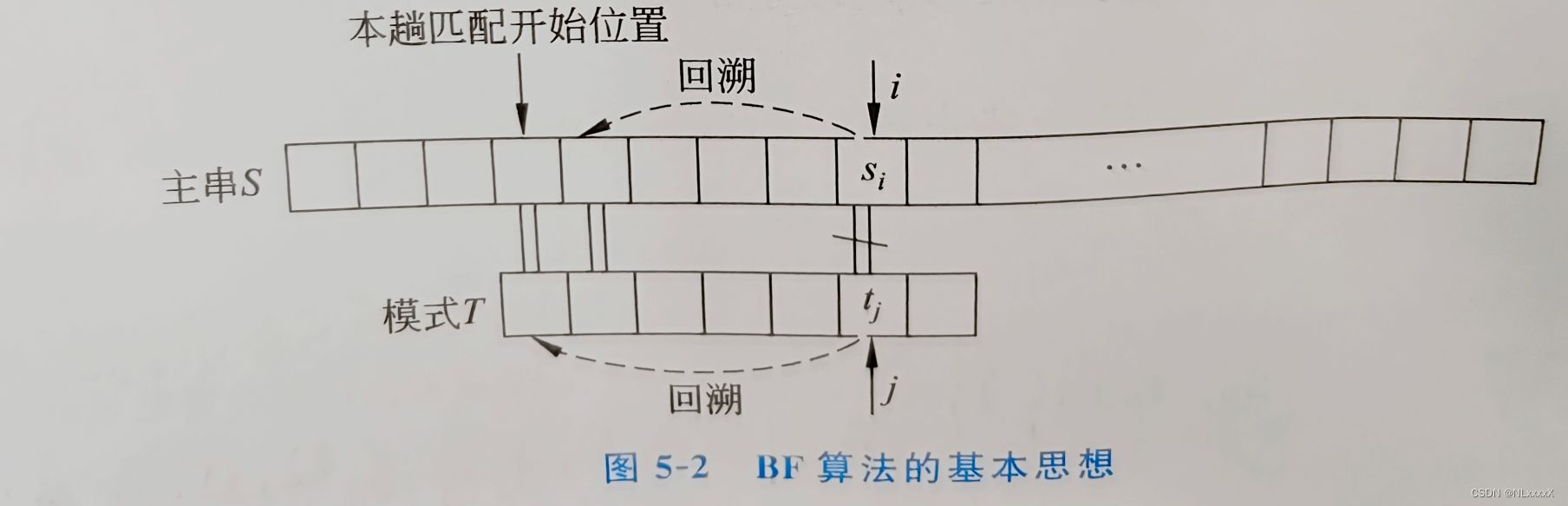
【想法1】 应用蛮力法解决串匹配问题的过程是：从主串 S 的第一个字符开始和模式T的第一个字符进行比较，若相等，则继续比较二者的后续字符；若不相等，则从主串S的第二个字符开始和模式T的第一个字符进行比较。重复上述过程，若T中的字符全部比较完毕，则说明本趟匹配成功;若 S中的字符全部比较完毕，则匹配失败。这个算法称为朴素的模式匹配算法，简称 BF算法，如图5-2所示。

设主串 S="abcabcacb",模式 T="abcac", BF算法的匹配过程如图5-3所示。

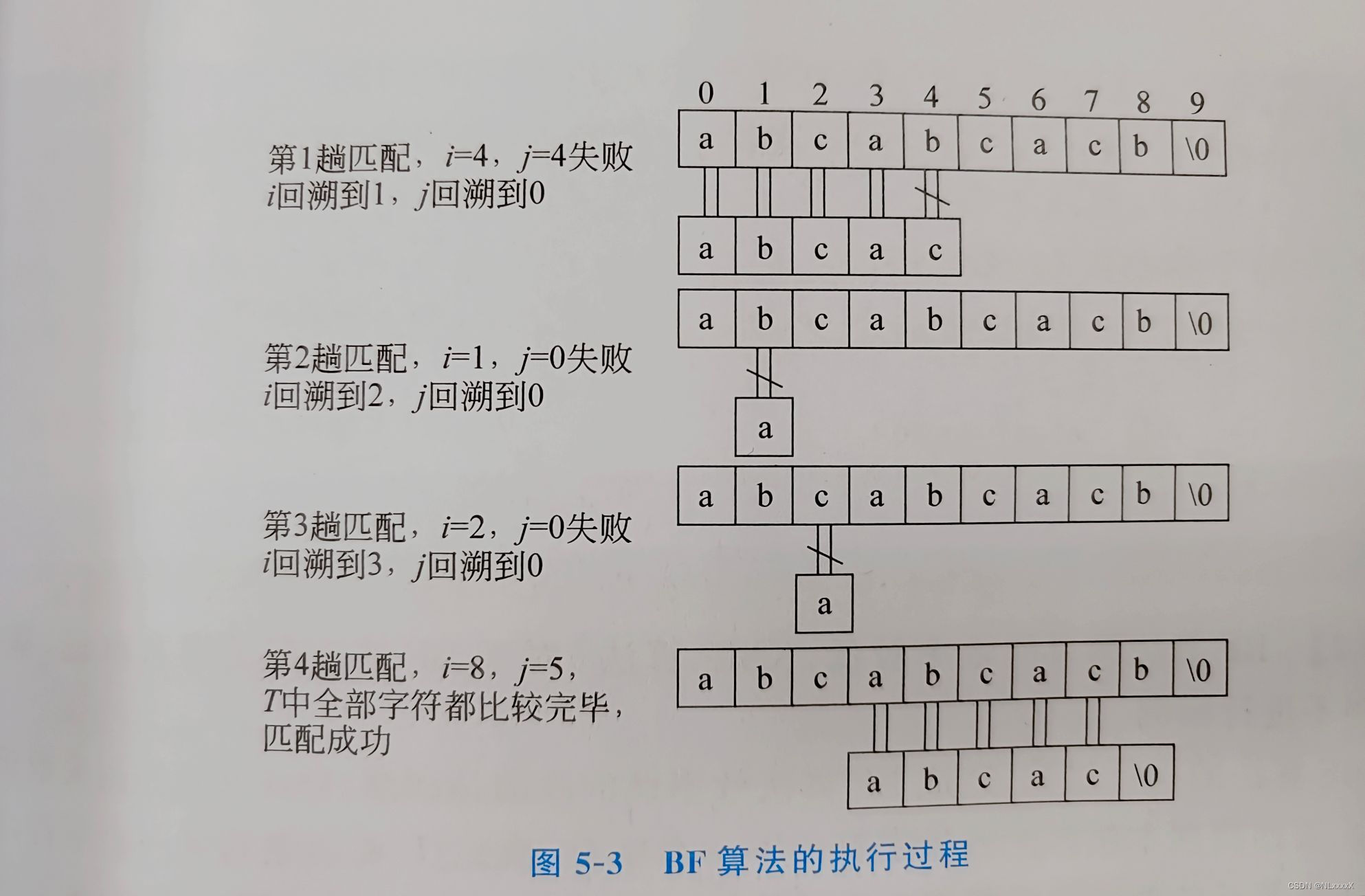
【算法1】 设字符数组 S 存放主串，字符数组T存放模式, BF算法如下。
算法：串匹配算法 BE

输人：主串 S,模式 T

输出：T在S中的位置
1.初始化主串比较的开始位置index=0;
2.在串 S 和串T中设置比较的起始下标i=0,j=0;
3.重复下述操作，直到S或T的所有字符均比较完毕：
3.1 如果 S[i]等于T[j],则继续比较S和T的下一对字符；
3.2 否则，下一趟匹配的开始位置index++,回溯下标i=index,j=0;
4.如果T中所有字符均比较完，则返回匹配开始位置的序号；否则返回0;

【算法分析1】 设主串S长度为n,模式T长度为m,在匹配成功的情况下，考虑最坏情况，即每趟不成功的匹配都发生在串T的最后一个字符。
例如：S= "aaaaaaaaaaab'"
T="aaab"
设匹配成功发生在si处，则在i-1趟不成功的匹配共比较了(i-1)×m次,第i趟成功的匹配共比较了m次，所以总共比较了ixm次，平均比较次数是：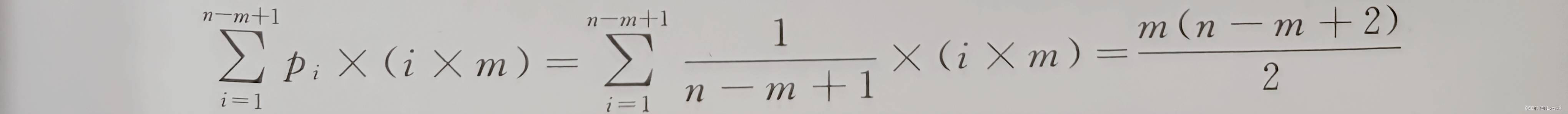

一般情况下，m<<n, 因此最坏情况下的时间复杂度是O(nXm)。
【算法实现1】设字符数组S和T分别存储主串和模式，程序如下

#include <iostream>
using namespace std;

int BF(char S[ ], char T[ ])
{
int index = 0, i = 0, j = 0;
while ((S[i] != '\0') && (T[j] != '\0'))
{
if (S[i] == T[j]) {i++; j++;}
else {index++; i = index; j = 0; } //i和j分别回溯
}
if (T[j] == '\0') return index + 1; //返回本趟匹配的开始位置
else return 0;
}
int main( )
{
char S[] = "abcabcacb";
char T[] = "abcac";
int index = BF(S, T);
// 在此处添加你想要执行的其他操作，例如输出匹配结果
std::cout << "匹配的起始位置：" << index << std::endl;
return 0;
}

【想法2】 BF算法简单但效率较低， KMP 算法对于BF 算法有了很大改进，基本思想是主串不进行回溯。
        分析BF算法的执行过程，造成 BF算法效率低的原因是回湖，即在某趟匹配失败后对于主串 S要回溯到本趟匹配开始字符的下一个字符，模式T要回溯到第一个字符，而这些回溯往往是不必要的。观察图5-3所示的匹配过程，在第1趟匹配过程中, S[0]~S[3]和T[0]~T[3]匹配成功,S[4]不等于T[4]匹配失败。因为在第1趟中有 S[1]=T[1], 而T[0]不等于T[1], 因此有T[0]不等于S[1], 所以第2趟是不必要的，同理第3趟也是不必要的，可以直接到第4趟。进一步分析第4趟中的第一对字符 S[3]和 T[0]的比较是多余的，因为第1趟中已经比较了 S[3]和 T[3]，并且 S[3]=T[3], 而 T[0]=T[3], 因此必有 S[3]=T[0], 因此第4趟比较可以从第二对字符 S[4]和 T[1]开始进行，这就是说，第1趟匹配失败后，下标i不回溯，而是将下标j回溯至第2个字符，从 T[1]和 S[4]开始进行比较。
        综上所述，希望某趟在 S[i]和T[j]匹配失败后，下标i不回溯，下标j回溯至某个位置k，从T[k]和 S[i]开始进行比较。显然，关键问题是如何确定位置k。
        观察部分匹配成功时的特征，某趟在S[i]和 T[j]匹配失败后，下一趟比较从 S[i]和T[k]开始，则有T[0]~T[k-1]=S[i-k]~S[i-1]成立,如图5-4(a)所示；在部分匹配成功时，有T[j-k]~T[j-1]-S[i-k]~S[i一1]成立，如图5-4(b)所示。

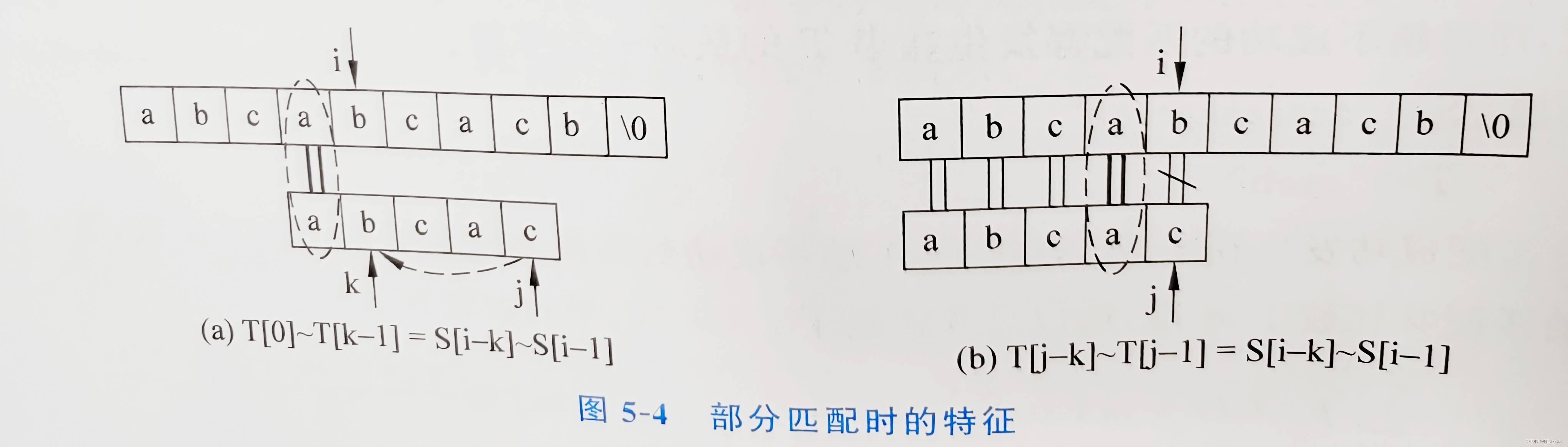
由T[0]~T[k-1]=S[i-k]~S[i-1]和T[j-k]~T[j-1]=S[i-k]~S[I-1],可得：

T[0]~ T[k-1]=T[j-k]~ T[j-1] (5-1)
式(5-1)说明，模式中的每一个字符T[j]都对应一个k值，这个k值仅依赖于模式本身，与主串无关，且 T[0]~T[k-1]是 T[0]~T[j-1]的真前缀, T[j-k]~T[j-1]是T[0]~T[j-1]的真后缀，k是T[0]~T[j-1]的真前缀和真后缀相等的最大子串的长度。用next[j]表示T[j]对应的k值(0<=j<m),定义如下：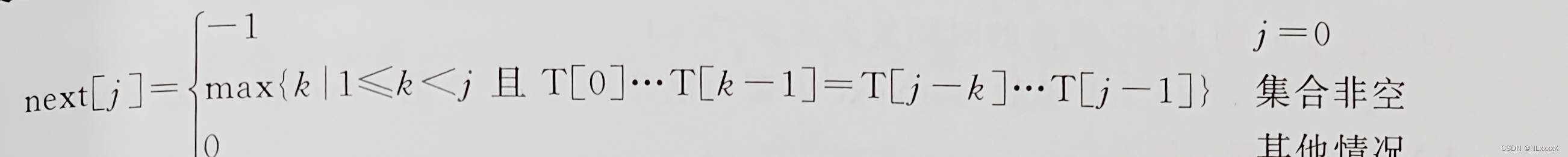

设模式 T="ababc",根据 next[j]的定义，计算过程如下：
j=0时, next[0]=-1
j=1时, next[1]=0
j=2时, T[0]≠T[1],则 next[2]=0
j=3时， T[0]T[1]≠T[1]T[2], T[0]=T[2], 则 next[3]=1
j=4时, T[0]T[1]T[2]≠T[1]T[2]T[3], T[0]T[1]=T[2]T[3], 则 next[4]=2
设主串 S="ababaababcb", 模式 T="ababc", 模式T的next值为(-1, 0,0,1, 2), KMP算法的匹配过程如图 5-5 所示。

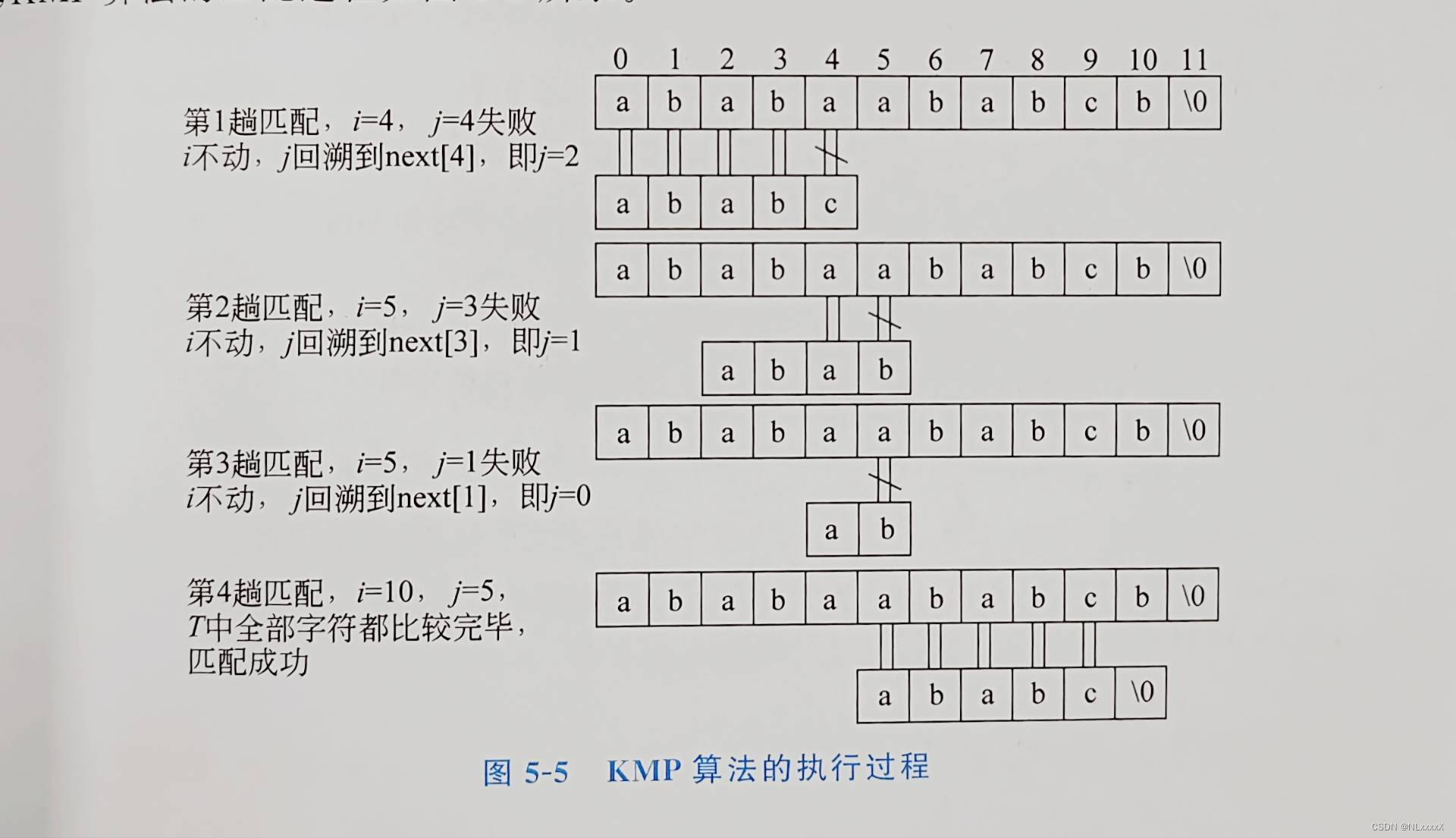
【算法 2】在求得了模式T的next值后,KMP算法如下。
算法：串匹配算法 KMP

输入：主串 S, 模式T

输出：T在S中的位置
1.在串 S和串T中分别设置比较的起始下标i=0, j=0;
2.重复下述操作，直到S或T的所有字符均比较完毕：
2.1如果 S[i]等于T[j]，则继续比较S和T的下一对字符；

2.2 否则，将下标j回溯到 next[j]位置，即j=next[j];
2.3 如果j等于-1,则将下标i和j分别加1,准备下一趟比较；
3.如果T中所有字符均比较完毕，则返回本趟匹配开始位置的序号；否则返回0；
【算法分析 2】 在求得模式T的next值后,KMP算法只需将主串扫描一遍，设主串的长度为n,则KMP算法的时间复杂度是O(n)。
【算法实现2】 设函数 GetNext用蛮力法求得模式 T的 next 值，函数 KMP 实现
KMP算法，程序如下。

#include <iostream>
using namespace std;

void GetNext(char T[ ], int next[ ])
{
int i, j, len;
next[0] = -1;
for (j = 1; T[j]!='\0'; j++) //依次求next[j]
{
for (len = j - 1; len >= 1; len--) //相等子串的最大长度为j-1
{
for (i = 0; i < len; i++) //比较T[0]~T[len-1]与T[j-len]~T[j-1]
if (T[i] != T[j-len+i]) break;
if (i == len) { next[j] = len; break;}
}
if (len < 1) next[j] = 0; //其他情况，无相等子串
}
}

int KMP(char S[ ], char T[ ]) //求T在S中的序号
{
int i = 0, j = 0;
int next[80]; //假定模式最长为80个字符
GetNext(T, next);
while (S[i] != '\0' && T[j] != '\0')
{
if (S[i] == T[j]) {i++; j++; }
else
{
j = next[j];
if (j == -1) {i++; j++;}
}
}
if (T[j] == '\0') return (i - j + 1); //返回本趟匹配的开始位置
else return 0;
}
int main( )
{
char S[] = "abcabcacb";
char T[] = "abcac";

int index = KMP(S, T);

// 输出匹配结果
if (index != 0) {
std::cout << "T 在 S 中匹配的起始位置是：" << index << std::endl;
} else {
std::cout << "T 在 S 中没有找到匹配项" << std::endl;
}

return 0;
}

5.3.1. 选择排序

【问题】 选择排序(selection sort)的基本思想是（第i趟排序在无序序列，ri~rn中找到值最小的记录，并和第i个记录交换作为有序序列的第i个记录;如图5-6所示。

【想法】 图5-7给出了一个选择排序的例子（无序区用方括号括起来），具体的排序
过程如下。
(1)将整个记录序列划分为有序区和无序区，初始时有序区为空，无序区含有待排序
的所有记录。
(2)在无序区查找值最小的记录，将它与无序区的第一个记录交换，使得有序区扩展一个记录，同时无序区减少一个记录。
(3) 重复执行步骤(2),直至无序区只剩下一个记录

【算法实现】设数组r[n]存储待排序记录序列，注意，数组下标从0开始，则第i个记录存储在r[i-1]中。程序如下。

#include <iostream>
using namespace std;

void SelectSort(int r[ ], int n)
{
int i, j, index, temp;
for (i = 0; i < n - 1; i++) //进行n-1趟选择排序
{
index = i;
for (j = i + 1; j < n; j++) //在无序区中查找最小记录
if (r[j] < r[index]) index = j;
temp = r[i]; r[i] = r[index]; r[index] = temp; //交换记录
}
}
int main( )
{
int r[]={1,6,7,5,3,8,9,2};
SelectSort(r, 8);
for (int i = 0; i < 8; i++)
std::cout << r[i] << " ";
return 0;
}