目录

一，3110. 字符串的分数

二，3111. 覆盖所有点的最少矩形数目

三，3112. 访问消失节点的最少时间​编辑

写法一：朴素 Dijkstra（适用于稠密图，即边比较多的图）

写法二：堆优化 Dijkstra（适用于稀疏图，即边比较少的图）

四，3113. 边界元素是最大值的子数组数目

---

一，3110. 字符串的分数

本题就是求相邻字符差值绝对值的和，从下标1开始遍历，计算 i 和 i-1 的差值绝对值，将其加起来就是答案。 

代码如下： 

class Solution {public int scoreOfString(String s) {int ans = 0;for(int i=1; i<s.length(); i++){ans += Math.abs(s.charAt(i)-s.charAt(i-1));}return ans;}
}

二，3111. 覆盖所有点的最少矩形数目

仔细读题可以发现，其实这题与纵坐标没有关系，只需要关注横坐标就行了，所以题目就变成了在 x2 - x1 <= w 的情况下，最少需要几个线段才能覆盖所有横坐标。

该题需要对横坐标进行排序，再遍历横坐标，用一个变量 r 来统计在以 x 为左端点时最大的右端点，即 r = x + w，当有 xi > r 时，就说明需要添加一个线段ans++，跟新 r = xi + w，直到跳出循环，返回ans

代码如下：

class Solution {public int minRectanglesToCoverPoints(int[][] points, int w) {Arrays.sort(points, (x,y)->x[0]-y[0]);//排序int ans = 0;int r = -1;for(int i=0; i<points.length; i++){if(r < points[i][0]){//跟新右端点和ansr = points[i][0] + w;ans++;}}return ans;}
}

三，3112. 访问消失节点的最少时间

本题求点到点最短路径，一道标准的 djstra算法题（注：该算法不适用于有负权重的图），简单说一下djstra算法的思路：从初始点出发，选出与初始点相邻且距离最近的点，再从初始点和选出的点出发，选出相邻且距离最近的点。（注：每次选出一个点，且该点不是之前选过的点）

这么说有点抽象，画个图理解一下：

 

可以发现，每次都会找到一个A ->  ? 的最短路径，也就是说只要循环 n-1 次，就可以找到A点到其他所有点的最短路径。而在代码实现过程中需要两个数组，一个数组来统计该点是否被访问过，一个数组统计 A->? 的最短路径。

这里先介绍两种写法：

模板一：朴素 Dijkstra（适用于稠密图，即边比较多的图）

class Solution {public int moban(int n, int[][] edges) {//稠密图建图推荐使用数组建图//注：根据题目建图，这里建的是无向图int[][] g = new int[n][n];for(int i=0; i<n; i++)Arrays.fill(g[i], Integer.MAX_VALUE/2);for(int[] e : edges){int x = e[0], y = e[1], w = e[2];g[x][y] = w;g[y][x] = w;}int[] dis = new int[n];//存储从0->i节点的最短路径Arrays.fill(dis, Integer.MAX_VALUE/2);//防溢出dis[0] = 0;//0->0路径为0boolean[] vis = new boolean[n];//统计i点是否已经选择过for(int i=0; i<n-1; i++){int x = -1;for(int j=0; j<n; j++){//找出未访问过的距离A点最近的点if(!vis[j]&&(x==-1 || dis[j]<dis[x])){x = j;}}vis[x] = true;//该路径即为0->x的最短路径for(int y=0; y<n; y++){//更新0->y的最短路径dis[y] = Math.min(dis[y], dis[x]+g[x][y]);//注：虽然会遍历到已经访问过的点，但是不会对结果造成影响}}return dis;}
}

模板二：堆优化 Dijkstra（适用于稀疏图，即边比较少的图）

class Solution {public int[] moban(int n, int[][] edges) {//稀疏图建议使用链表建图//注：根据题目建图，这里是无向图List<int[]>[] g = new ArrayList[n];Arrays.setAll(g, e->new ArrayList<>());for(int[] e : edges){int x = e[0], y = e[1], w = e[2];g[x].add(new int[]{y, w});g[y].add(new int[]{x, w});}int[] dis = new int[n];//0->i的最短路径Arrays.fill(dis, -1);dis[0] = 0;PriorityQueue<int[]> que = new PriorityQueue<>((x,y)->x[0]-y[0]);//小根堆que.offer(new int[]{0, 0});//(t,j)->t:路径，j:节点while(!que.isEmpty()){int[] poll = que.poll();int dx = poll[0];int x = poll[1];if(dx > dis[x])//堆的懒删除continue;for(int[] y : g[x]){int newDis = dis[x] + y[1];if(dis[y[0]]==-1 || newDis < dis[y[0]]){//更新与x点相邻的点的最短路径dis[y[0]] = newDis;que.offer(new int[]{newDis, y[0]});}}}return dis;} 
}

 本题代码如下：

class Solution {public int[] minimumTime(int n, int[][] edges, int[] disappear) {List<int[]>[] g = new ArrayList[n];Arrays.setAll(g, e->new ArrayList<>());for(int[] e : edges){int x = e[0], y = e[1], w = e[2];g[x].add(new int[]{y, w});g[y].add(new int[]{x, w});}int[] dis = new int[n];Arrays.fill(dis, -1);dis[0] = 0;PriorityQueue<int[]> que = new PriorityQueue<>((x,y)->x[0]-y[0]);que.offer(new int[]{0, 0});//(t,j)->t:时间，j:节点while(!que.isEmpty()){int[] poll = que.poll();int dx = poll[0];int x = poll[1];if(dx > dis[x])continue;for(int[] y : g[x]){int newDis = dis[x] + y[1];//本题多了一个条件，所以这里多了个判断if(newDis < disappear[y[0]] && (dis[y[0]]==-1 || newDis < dis[y[0]])){dis[y[0]] = newDis;que.offer(new int[]{newDis, y[0]});}}}return dis;} 
}

四，3113. 边界元素是最大值的子数组数目

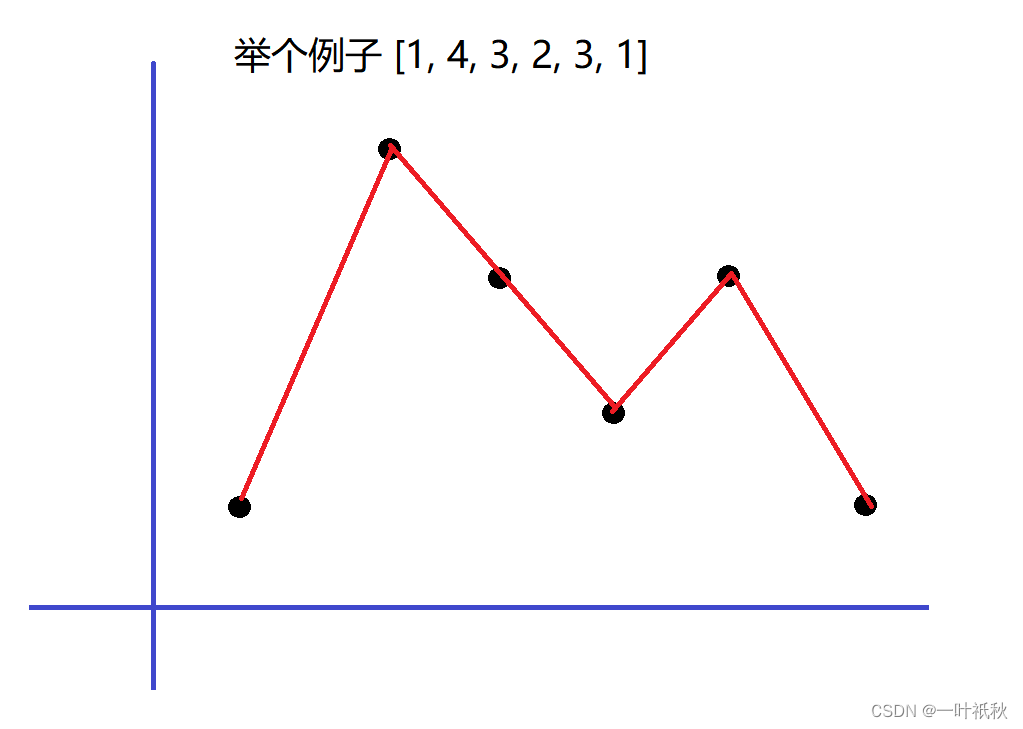
本题本质上还是一道单调栈的题，画个图理解一下：

从左往右依次遍历：

• [1]时，有[1]成立
• [1,4]时，多出[4]成立，这时候1就成了垃圾数据，因为如果包含1，那么这个数组不可能满足题意。删去1
• [4,3]时，多出[3]成立，这时4不能删去，因为右端可能出现一个4，使其满足题意
• [4,3,2]时，多出[2]成立，这时2不能删去，因为右端可能出现一个2，使其满足题意
• [4,3,2,3]时，多出[3][3,2,3]成立，这时2就成了垃圾数据，因为如果包含2，那么这个数组不可能满足题意。删去2
• [4,3,3,1]时，多出[1]

可以发现[4,3,3,1]是单调减的，所以可以使用单调栈来解决该问题。

代码如下：

class Solution {public long numberOfSubarrays(int[] nums) {long ans = 0;Deque<int[]> que = new ArrayDeque<>();que.add(new int[]{Integer.MAX_VALUE, 0});//防止que为空for(int num : nums){while(que.getLast()[0]<num){que.removeLast();}if(que.getLast()[0] == num)que.addLast(new int[]{num, que.getLast()[1]+1});elseque.addLast(new int[]{num, 1});ans += que.getLast()[1];}return ans;}
}