力扣题目链接
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;// dp[i]中的i表示背包内总和// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了vector<int> dp(10001, 0);for (int i = 0; i < nums.size(); i++) {sum += nums[i];}// 也可以使用库函数一步求和// int sum = accumulate(nums.begin(), nums.end(), 0);if (sum % 2 == 1) return false;int target = sum / 2;// 开始 01背包for(int i = 0; i < nums.size(); i++) {for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}// 集合中的元素正好可以凑成总和targetif (dp[target] == target) return true;return false;}
};想不到啊,想不到!
思路
这道题目初步看,和如下两题几乎是一样的,大家可以用回溯法,解决如下两题
- 698.划分为k个相等的子集
- 473.火柴拼正方形
这道题目是要找是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
那么只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了。
本题是可以用回溯暴力搜索出所有答案的,但最后超时了,也不想再优化了,放弃回溯,直接上01背包吧。
如果对01背包不够了解,建议仔细看完如下两篇:
- 动态规划:关于01背包问题,你该了解这些!(opens new window)
- 动态规划:关于01背包问题,你该了解这些!(滚动数组)(opens new window)
#01背包问题
背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。
要注意题目描述中商品是不是可以重复放入。
即一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,写法还是不一样的。
要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。
那么来一一对应一下本题,看看背包问题如何来解决。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
以上分析完,我们就可以套用01背包,来解决这个问题了。
动规五部曲分析如下:
- 确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中每一个元素的数值既是重量,也是价值。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
有录友可能想,那还有装不满的时候?
拿输入数组 [1, 5, 11, 5],举例, dp[7] 只能等于 6,因为 只能放进 1 和 5。
而dp[6] 就可以等于6了,放进1 和 5,那么dp[6] == 6,说明背包装满了。
- 确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
- dp数组如何初始化
在01背包,一维dp如何初始化,已经讲过,
从dp[j]的定义来看,首先dp[0]一定是0。
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
本题题目中 只包含正整数的非空数组,所以非0下标的元素初始化为0就可以了。
代码如下:
// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200
// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了
vector<int> dp(10001, 0);
- 确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中就已经说明:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
代码如下:
// 开始 01背包
for(int i = 0; i < nums.size(); i++) {for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}
}
- 举例推导dp数组
dp[j]的数值一定是小于等于j的。
如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。
用例1,输入[1,5,11,5] 为例,如图:
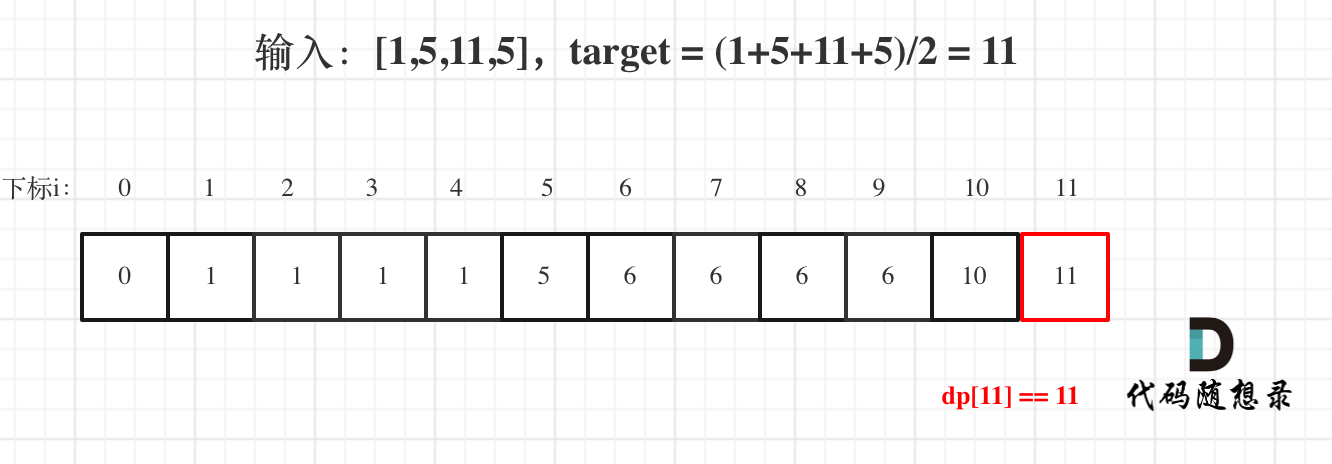
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
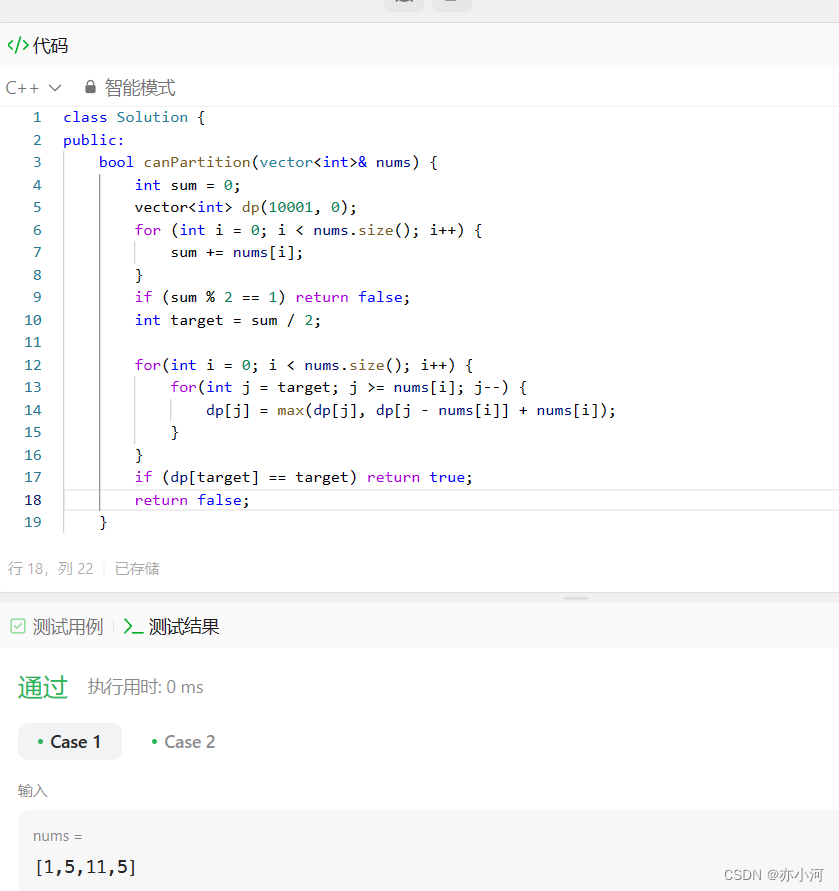
自己的思路:
一开始根本就不知道用背包啊
![[C语言][数据结构][链表] 单链表的从零实现!](https://img-blog.csdnimg.cn/direct/81f4f5409c814fe2a26c22c12cdd327c.png)


![[大模型]Langchain-Chatchat安装和使用](https://img-blog.csdnimg.cn/img_convert/85e9661b26c5b5bd6b425c6d4f3df1db.jpeg)