Boosting the Speed of Entity Alignment 10×: Dual Attention Matching Network with Normalized Hard Sample Mining

将实体对齐速度提高 10 倍：具有归一化硬样本挖掘的双重注意力匹配网络

ABSTRACT

寻找多源知识图谱(KG)中的等效实体是知识图谱集成的关键步骤，也称为实体对齐(EA)。然而，大多数现有的 EA 方法效率低下且可扩展性差。最近的总结指出，其中一些甚至需要几天的时间来处理包含 200000 个节点(DWY100K)的数据集。我们认为过度复杂的图编码器和低效的负采样策略是两个主要原因。在本文中，我们提出了一种新颖的知识图谱编码器——双重注意力匹配网络(Dual-AMN)，它不仅可以智能地对图内和跨图信息进行建模，而且还大大降低了计算复杂度。此外，我们提出了 标准化硬样本挖掘损失(*NormalizedHardSample Mining Loss)*来平滑地选择具有减少损失偏移的硬负样本。在广泛使用的公共数据集上的实验结果表明，我们的方法实现了高精度和高效率。在DWY100K上，我们的方法的整个运行过程可以在1100秒内完成，比以前的工作至少快10倍。我们的方法在所有数据集上的性能也优于以前的工作，其中 Hits@1 和 MRR 已从 6% 提高到 13%。

1 INTRODUCTION

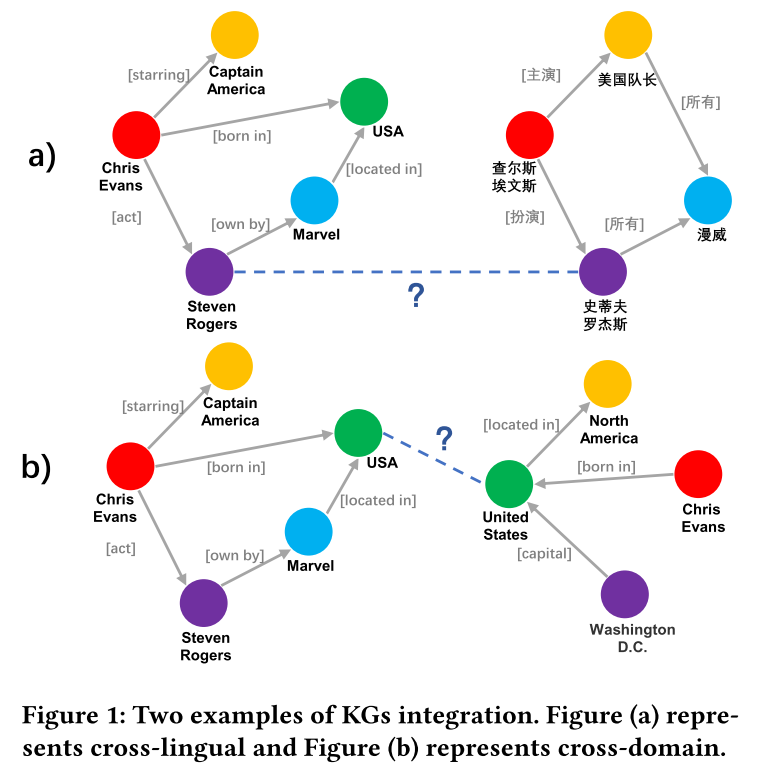
导致先进方法时间复杂度高的主要原因有两个：

1. 过于复杂的图编码器：每次在普通GCN中引入复杂的技术，例如图注意力机制、图匹配网络(GMN)、联合学习，时间复杂度都会急剧增加。
2. 低效的负采样策略：几乎所有现有的 EA 方法都依赖于成对损失函数。在成对损失中，负样本是通过均匀随机采样构建的。这样，样本通常是高度冗余的并且信息有限。学习过程可能会受到低质量负样本的阻碍，导致收敛缓慢和模型退化。

在本文中，提出了双重注意力匹配网络（Dual-AMN）来捕获单个图内和跨两个图的双重关系信息，而不是为了更好的性能而牺牲效率：简化的关系注意层通过生成关系来捕获每个知识图谱内的关系信息 -通过关系各向异性注意和关系投影进行特定嵌入。代理匹配注意层将对齐视为一种特殊的关系类型，并通过代理向量对其进行显式建模。此外，为了解决低效采样问题，提出了归一化硬样本挖掘损失。首先，LogSumExp 运算用于逼近 Max 运算，以平滑而高效地生成硬样本。然后，为了解决 LogSumExp 中超参数选择的困境，引入了动态调整损失分布的损失归一化策略。

主要贡献总结如下：

• 模型。 提出了一种新颖的图编码器双注意力匹配网络（Dual-AMN），由简化关系注意力层和代理匹配注意力层组成。所提出的编码器不仅可以智能地对图内和跨图关系进行建模，而且还大大降低了计算复杂度。
• 训练。 提出了归一化硬样本挖掘损失（Normalized Hard Sample Mining Loss），而不是低效的采样策略，其中 LogSumExp 操作有效地生成硬样本，并且损失归一化缓解了超参数选择的困境。新的损失极大地减少了采样消耗并加快了模型的收敛速度。
• 实验。 在广泛使用的公共数据集上的实验结果表明，我们的方法具有较高的效率和准确性。此外，我们设计了许多辅助实验来证明每个组件的有效性和模型的可解释性。

2 TASK DEFINITION

知识图的定义：KG的正式定义是一个有向图$G=(E,R,T)$，实体E、关系R和三元组$T\subseteq E\times R\times E$。

实体对齐的定义：给定两个KG $G_1=(E_1,R_1,T_1),G_2=(E_2,R_2,T_2)$，以及一个预对齐的实体对集合$P=\{(u,v)|u\in E_1,u\in E_2,u\equiv v\}$，其中$ \equiv$ 表示等价。 EA的目的是根据$G_1,G_2,P$的信息获得更多潜在的等价实体对。

3 RELATED WORK

现有 EA 方法可以抽象为一个包含三个主要组件的框架：

• 图嵌入模块负责将知识图谱的实体和关系编码为密集嵌入。
• 实体对齐模块旨在通过预对齐的实体对将多源知识图谱的嵌入映射到统一的向量空间中。
• 信息增强模块能够生成半监督数据或引入额外的文字信息进行增强。

3.1 Embedding Module

TransE、GNN 和 Hybrid 是三种主流的嵌入方法。

TransE 将关系解释为从头部实体到尾部实体的转换，并假设如果三元组 (h, r, t) 成立，则实体和关系的嵌入遵循假设 $h+r\approx t$。

GNN 通过聚合实体的邻近信息来生成节点感知嵌入。

3.2 Alignment Module

最常见的对齐方法如下：

1. 映射使用一个或两个线性变换矩阵将不同KG中实体的嵌入映射到统一的向量空间。
2. 语料库融合交换预对齐集中的实体并生成新的三元组以将嵌入校准到统一空间中。
3. Margin-based表示一系列成对的基于margin的损失函数，大多数都使用基于 Margin 的损失作为其对齐模块。

3.3 Enhancement Module

1. 现有方法通常保留 30% 甚至更少的对齐对作为训练数据来模拟这种情况。
2. 一些 EA 方法 采用自助法迭代生成半监督数据。
3. 除了结构之外，一些方法提出引入文字信息可以为对齐模型提供多方面视图并提高准确性。

4 DUAL ATTENTION MATCHING NETWORK

Dual-AMN 由两个主要组件组成：简化关系注意层和代理匹配注意层。简化关系注意力层通过关系各向异性注意力和关系投影生成特定于关系的嵌入，捕获每个知识图谱内的关系信息。通过将对齐视为特殊关系，代理匹配注意层利用代理列表来显式捕获跨图信息。通过结合这两个提出的组件的结果，Dual-AMN 不仅巧妙地嵌入图内和跨图关系，而且还大大降低了计算复杂度。

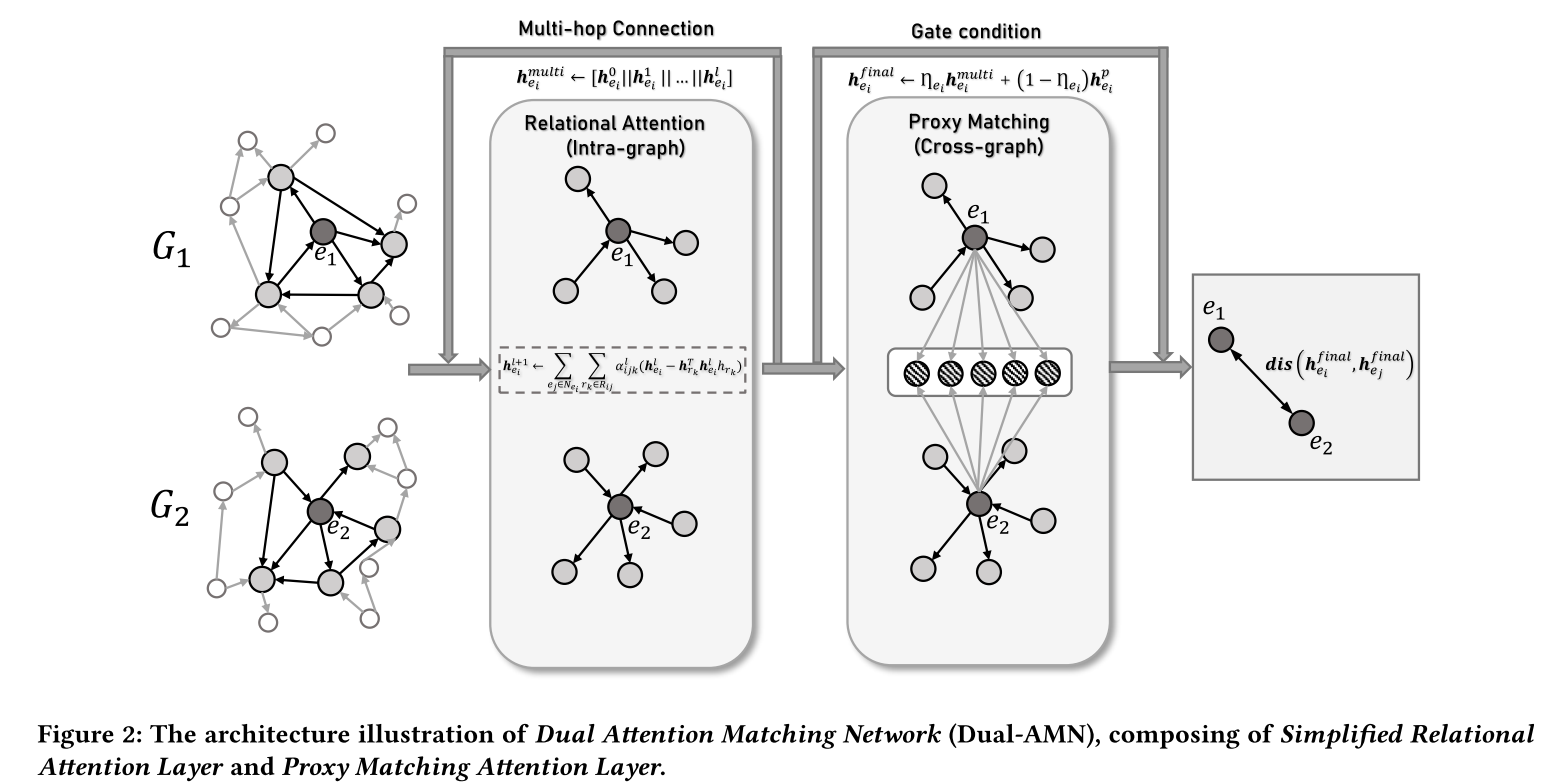
4.1 Simplified Relational Attention Layer

由于普通 GCN 无法对知识图谱中的异构关系信息进行建模，因此在 EA 任务中提出了许多关系感知的 GNN 变体。其中大多数可以用以下等式描述：

h e i l + 1 = ∑ e j ∈ N e i ∪ { e i } α i j W h e j l h_{e_i}^{l+1}=\sum_{e_j\in\mathcal{N}_{e_i}\cup\{e_i\}}\alpha_{ij}W\boldsymbol{h}_{e_j}^l hei​l+1​=ej​∈Nei​​∪{ei​}∑​αij​Whej​l​

其中$h_{e_i}^l$表示第l层GNN层得到的嵌入向量 $e_i$，${\alpha }_{i,j}$表示 $e_i$和 $e_j$之间的权重系数，$\mathbf{W}$表示变换矩阵。

设计了一个简化的关系感知 GNN 层。模型的输入是两个度量，$H^e\in {\mathbb{R}}^{|E|\times d}$代表初始实体特征，$H^r\in {\mathbb{R}}^{|R|\times d}$代表初始关系特征。它们都是由 He初始化随机初始化的。与现有的 EA 方法类似，使用各向异性关系注意机制来聚合实体周围的邻域信息。 第$l$层实体$e_i$的输出嵌入由以下等式获得：
$${\mathbf{h}}_{e_i}^{l+1}=tanh(\sum _{e_j\in {\mathcal{N}}_{e_i}}\sum _{r_k\in {\mathcal{R}}_{ij}}{\alpha }_{ijk}^l({\mathbf{h}}_{e_j}^l-2{\mathbf{h}}_{r_k}^T{\mathbf{h}}_{e_j}^l{\mathbf{h}}_{r_k}))$$

使用 $tanh$ 作为激活函数。使用关系投影运算来代替标准线性变换矩阵$\mathbf{W}$。 这种操作无需额外参数即可为每个实体生成关系特定的嵌入。对于${\alpha }_{ijk}$的计算，采用元路径机制来分配权重：

$${\alpha }_{ijk}^l=\frac{exp({\mathbf{\upsilon }}^T{\mathbf{h}}_{{\mathbf{r}}_k})}{{\sum }_{e_j^{\prime }\in {\mathcal{N}}_{e_i}}{\sum }_{r_{k^{\prime }}\in {\mathcal{R}}_{i{j}^{\prime }}}exp({\mathbf{\upsilon }}^T{\mathbf{h}}_{r_{k^{\prime }}})}$$

其中${\mathbf{v}}^T$是注意力向量。Softmax操作从连接到实体的所有类型的边中选择最关键的路径（即元路径），它嵌入了关系各向异性但最大程度地简化了计算。

在之前的研究中，GNN能够通过堆叠更多层来扩展到多跳相邻级别信息，从而创建更具全局意识的图表示。按照这个想法，将不同层的嵌入连接在一起以获得实体 $e_i$ 的多跳嵌入：

$${\mathbf{h}}_{e_i}^{multi}=[h_{e_i}^0\Vert h_{e_i}^1\Vert ...\Vert h_{e_i}^l]$$

其中$\Vert$表示连接操作。

4.2 Proxy Matching Attention Layer

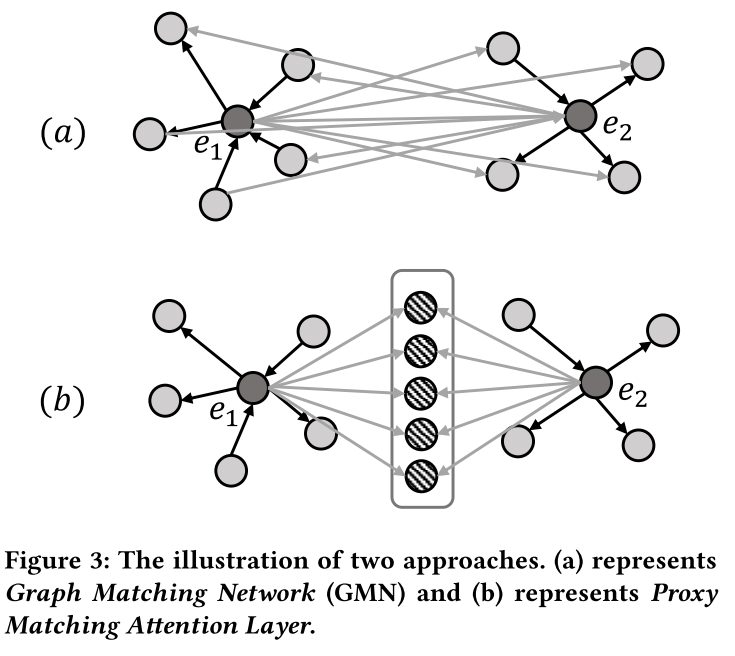
图匹配网络(GMN) 构建了一个跨图注意机制来学习相似性，尽管他们将对齐纯粹视为节点到节点的交互（如图 3(a) 所示）。这种节点到节点的交互强制在一对上共同学习嵌入，但代价是大量额外的计算效率。由于两个图中的每对节点都需要注意力权重，因此该操作的计算成本为 $O(|E_1||E_2|)$。

提出了代理匹配注意力层。如图3(b)所示，使用一组有限的代理向量来表示跨图对齐关系，类似于使用锚点来呈现空间。如果两个实体是等价的，那么它们与这些代理向量相关的相似度分布也应该是一致的。通过这种方式，所提出的层能够捕获跨图对齐信息，而无需计算节点到节点的交互。代理匹配注意力层的交互作用是计算所有实体与有限锚点之间的相似度，类似于聚类。在大规模 KG 或密集图上，这种交互方法可以大大降低计算复杂度，从 $O(|E_1||E_2|)$ 降低到 $O(|E_1|+|E_2|)$。

代理匹配注意力层的输入是两个矩阵：$H^{multi}\in {\mathbb{R}}^{|E|\times ld}$表示简化关系注意力层获得的实体嵌入，$Q\in {\mathbb{R}}^{n\times ld}$表示随机初始化的代理向量，其中 $n$ 表示代理向量的数量。就像 GMN 一样，第一步是计算每个实体与所有代理向量之间的相似度：

$${\beta }_{ij}=\frac{\exp (\cos ({\mathbf{h}}_{e_i}^{multi},{\mathbf{q}}_j))}{{\sum }_{k\in S_p}\exp (\cos ({\mathbf{h}}_{e_i},{\mathbf{q}}_k))}$$

$S_p$ 表示代理向量的集合。这里我们使用余弦度量来衡量嵌入之间的相似度。然后，实体 $e_i$ 的跨图嵌入可以计算为：

$${\mathbf{h}}_{e_i}^p=\sum _{j\in S_p}{\beta }_{ij}({\mathbf{h}}_{e_i}^{multi}-{\mathbf{q}}_j)$$

${\mathbf{h}}_{e_i}^p$ 直观地描述了 ${\mathbf{h}}_{e_i}^{multi}$ 与所有代理向量之间的差异。最后，我们采用门机制来组合 ${\mathbf{h}}_{e_i}^{multi}$和 ${\mathbf{h}}_{e_i}^p$，控制单图和多图之间的信息流：

$${\mathbf{\eta }}_{e_i}=sigmoid(\mathbf{M}{\mathbf{h}}_{e_i}^p+\mathbf{b})$$

$${\mathbf{h}}_{e_i}^{final}={\mathbf{\eta }}_{e_i}\cdot {\mathbf{h}}_{e_i}^p+(1-{\mathbf{\eta }}_{e_i})\cdot {\mathbf{h}}_{e_i}^p$$

$\mathbf{M}$ 和 $\mathbf{b}$是门权重矩阵和门偏置向量。

5 NORMALIZED HARD SAMPLE MINING 标准化硬样本挖掘

5.1 Smooth Hard Sample Mining 光滑硬样本挖掘

成对损失中的负样本是通过均匀随机抽样产生的，但这类样本是高度冗余的，并且包含太多容易甚至是无信息的样本。使用这种低质量的负样本进行训练可能会显着降低模型的学习能力并减慢收敛速度。一个简单但有效的策略是选择正样本周围的K-最近邻作为负样本，这也被称为硬样本挖掘。BootEA提出了基于这种策略的截断均匀负采样(TUNS)。

在深度度量学习领域，一些研究提出使用LogSumExp运算来平滑地生成硬负样本：

$$L=log\left[1+\sum _{i\in P}\sum _{j\in N}exp(\lambda (\gamma +s_i-s_j))\right]$$

其中$P$表示锚的正样本集，$N$表示负样本集。$\lambda$是比例因子。

当 $\lambda$被设置为适当的值时，LogSumExp可以取代$K$最近采样策略来生成高质量的负样本。当$\lambda =1$时，损失函数等价于具有交叉熵损失的Softmax。

5.2 Loss Normalization 损失归一化

使用归一化步骤来固定样本损失的均值和方差，并减少对超参数规模的依赖。 总体损失函数定义如下：

$$\begin{array}{rl}L& =\sum _{(e_i,e_j)\in P}log\left[1+\sum _{e_j^{\prime }\in E_2}exp(\lambda l_n(e_i,e_j,e_j^{\prime })+\tau )\right]\\ & +\sum _{(e_i,e_j)\in P}log\left[1+\sum _{e_i^{\prime }\in E_1}exp(\lambda l_n(e_j,e_i,e_i^{\prime })+\tau )\right]\end{array}$$

$l_n(e_i,e_j,e_j^{\prime })$ 表示三元组 $(e_i,e_j,e_j^{\prime })$ 的归一化损失。 $\tau$和${\lambda }^2$分别表示归一化损失的新均值和新方差。 $l_n(e_i,e_j,e_j^{\prime })$ 定义如下：

$$l_n(e_i,e_j,e_j^{\prime })=\frac{l_o(e_i,e_j,e_j^{\prime })-\mu (e_i,e_j)}{\sqrt{{\sigma }^2(e_i,e_j)-ϵ}}$$

$$l_o(e_i,e_j,e_j^{\prime })=\gamma +sim(e_i,e_j)-sim(e_i,e_j^{\prime })$$

其中 $l_o(e_i,e_j,e_j^{\prime })$表示三元组$(e_i,e_j,e_j^{\prime })$的原始损失，$\mu$和${\sigma }^2$表示原始损失的均值和方差，其计算公式为：

$$\mu (e_i,e_j)=\frac{1}{|E_2|}\sum _{e_i^{\prime }\in E_2}{l}_o(e_i,e_j,e_j^{\prime })$$

$${\sigma }^2(e_i,e_j)=\frac{1}{|E_2|}\sum _{e_j^{\prime }\in E_2}{\left[l_o(e_i,e_j,e_j^{\prime })-\mu (e_i,e_j)\right]}^2$$

$l_n(e_j,e_i,e_i^{\prime })$ 的计算过程与$l_n(e_i,e_j,e_j^{\prime })$ 类似。

在训练过程中，选择L2距离作为衡量实体之间相似度的指标：

$$sim(e_i,e_j)=\Vert h_{e_i}^{final}-h_{e_j}^{final}{\Vert }_2^2$$

在测试过程中，为了解决高维空间中的中心度问题，将CSLS设置为距离度量。注意，在训练中，$\sigma$和$\mu$不会参与梯度计算和反向传播。这是因为损失归一化旨在改变样本的权重，而不是梯度方向。如果 $\sigma$ 和 $\mu$ 在反向传播步骤中更新，损失将无法收敛。

6 EXPERIMENTS

6.1 Datasets

随机分割30%的预对齐实体对用于训练和开发，剩余的70%用于测试。

DBP15K、DWY100K、SRPRS

6.2 Baselines

**(1)Basic：**此类方法仅使用数据集中的原始结构信息（即三元组），不引入任何额外的增强模块：MTransE、GCN-Align、RSNs、MuGNN、KECG。

**(2)Semi-supervised：**这些方法采用引导来生成半监督结构数据：BootEA、NAEA、TransEdge和MRAEA。

**(3)Literal：**为了获得多方面视图，literal方法使用实体的文字信息（例如实体名称）作为输入特征：GM-Align，RDGCN，HMAN，HGCN。

三个相应的版本：(1)Dual-AMN是基本版本，没有任何增强模块。(2)Dual-AMN(Semi)引入 MRAEA 提出的双向迭代策略生成半监督数据。(3)Dual-AMN(Lit)采用简单的策略来利用文字信息。对于 $e_i\in K{G}_1$ 和 $e_j\in K{G}_2$，使用 Dual-AMN (Semi) 来获得结构相似度 $s_{ij}$。然后，使用跨语言词嵌入计算字面相似度$l_{ij}$ 。最后，根据$l_{ij}+s_{ij}$ 对实体进行排名。

6.3 Experimental Settings

使用 Hits@k 和平均倒数排名 (MRR) 作为评估指标。

超参数：对于所有数据集，使用相同的配置：嵌入的维数 $d=100$；GNN 的深度 $l=2$； 代理向量的数量 $n=64$；余量 $\gamma =1$；归一化损失的新均值和新方差为 $\tau =10$ 和 $\lambda =30$；批量大小为 1024；辍学率设定为30%。采用RMSprop优化模型，学习率为0.005。

6.4 Main Experiments

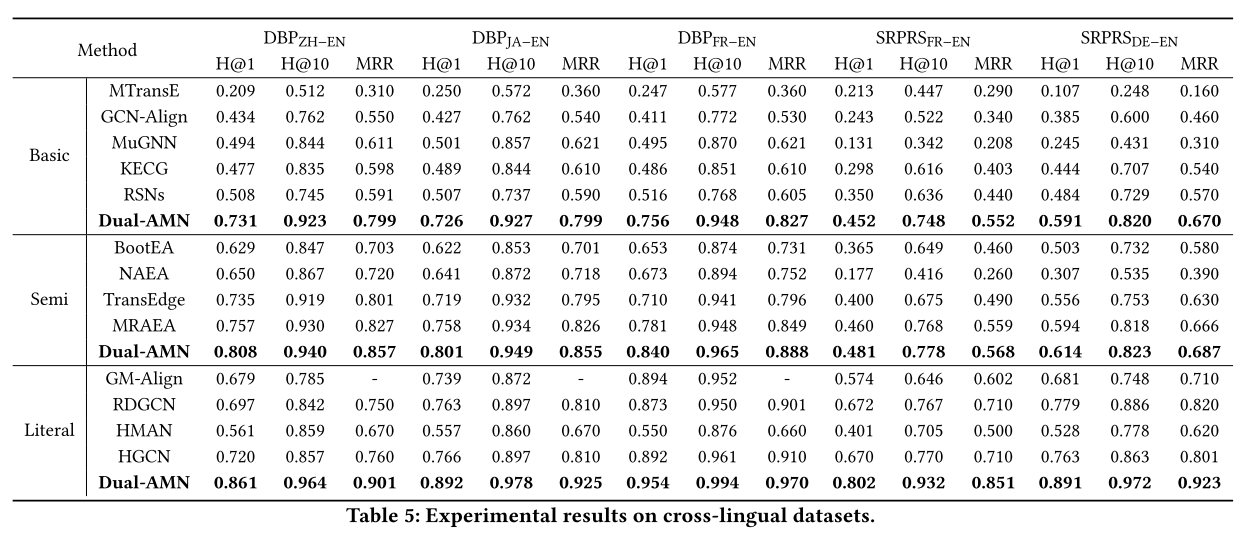
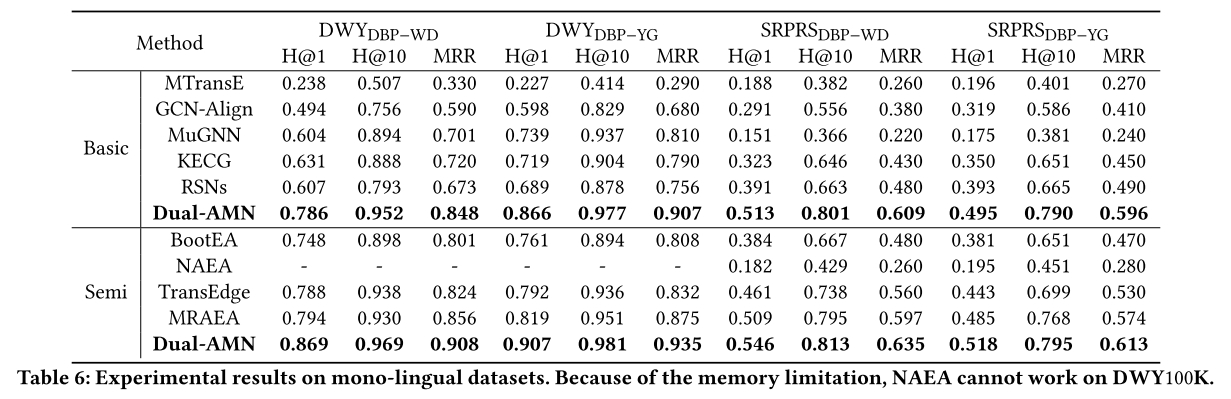
Dual-AMN 与基本方法。 Dual-AMN在所有数据集上始终达到最佳性能。

Dual-AMN 与半监督方法。 受益于半监督策略为下一轮训练生成更多标记数据，半监督方法的整体性能超过了基本方法。半监督策略在密集数据集上表现良好，而在稀疏数据集上的改进则微乎其微。

Dual-AMN 与文字方法。 由于单语言知识图谱之间的实体名称几乎相同，编辑距离算法可以实现真实性能。因此，文字方法仅在跨语言数据集上进行实验。

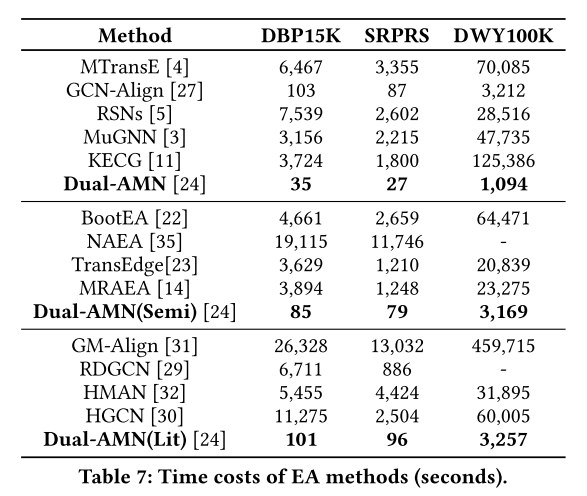
Dual-AMN的效率远远超过竞争对手。Dual-AMN的高效率使得大规模KG上的实体对齐应用成为可能。

6.5 Ablation Experiment 消融实验

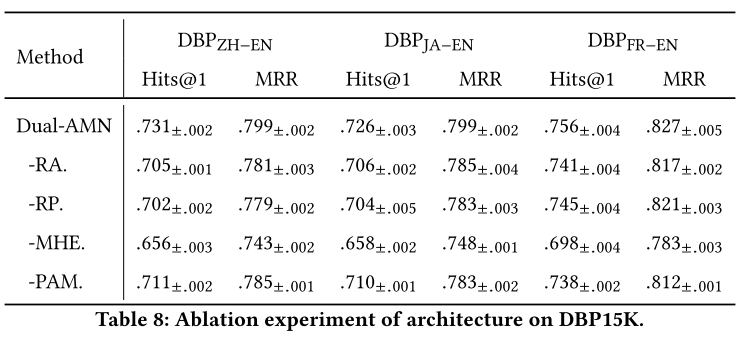
**结构消融实验。**Dual-AMN采用以下四个组件来捕获知识图谱中存在的多方面信息：(1)关系注意机制(RA)发现实体周围的关键路径。(2)关系投影操作(RP)生成实体的关系特定嵌入。(3)多跳嵌入 (MHE) 创建更具全局意识的知识图谱表示。(4)代理注意力匹配层(PAM)捕获跨图信息。表 8 报告了从 Dual-AMN 中移除这些组件后的平均值±标准的性能。在所有这些组件中，MHE 对性能的影响最大。平均而言，采用这些技术可以将性能提高 2% 到 3%。通过采用这些新设计，Dual-AMN进一步突破了EA精度的天花板。

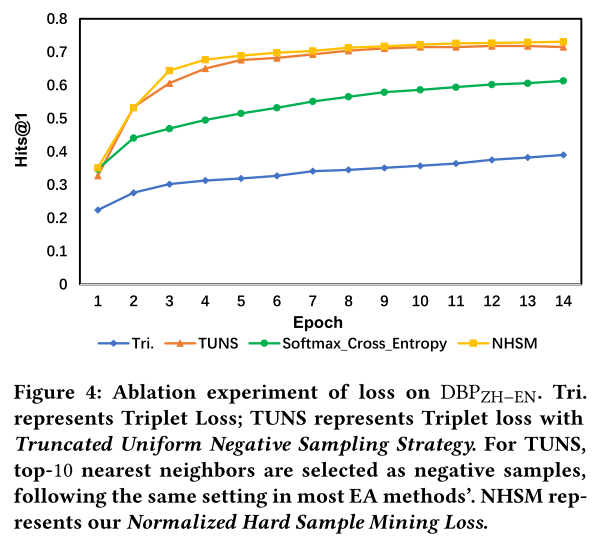
损失消融实验。 除了架构之外，标准化硬样本挖掘损失也是主要贡献之一。为了验证其有效性，将其与几种常见的损失函数进行比较。这些实验结果表明，所提出的损失函数在不损失任何精度的情况下显着提高了收敛速度。

6.6 Relation Interpretability 关系可解释性

除了性能和速度优势之外，Dual-AMN还具有一定程度的可解释性。由于相邻实体的权重是由它们之间的关系决定的，因此这些权重可以在一定程度上反映不同关系的重要性。每个关系的重要性通过以下等式获得：

$$I_{r_k}=v^T{h}_{r_k}$$

在 DWYYG 上训练模型并输出关系的重要性 $I_{rk}$。根据 $I_{rk}$ 对关系进行聚类。具有高重要性的关系（即元路径）通常能够识别另一个实体。

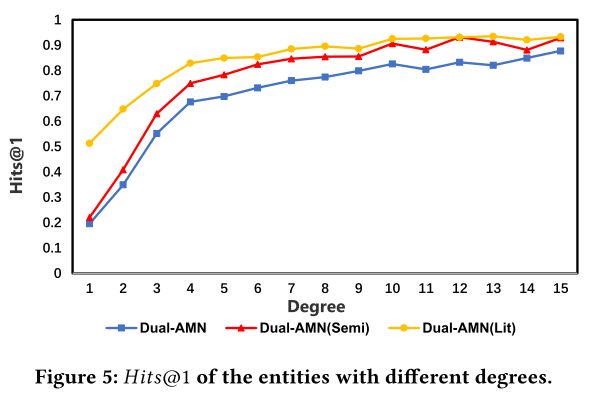
6.7 Degree Analysis 度分析

随着度数的增加，模型性能显着提高。半监督策略的引入提高了模型的整体性能，文字信息的结合也能有效提高这些稀疏实体的准确性。

7 CONCLUSION

过于复杂的图编码器和低效的负采样策略导致现有 EA 方法普遍效率低下，导致难以应用于大规模 KG。在本文中，我们提出了一种新颖的 KG 编码器双注意力匹配网络(Dual-AMN)，它不仅可以智能地建模图内和跨图关系，而且还大大降低了计算复杂度。为了取代低效的采样策略，我们提出归一化硬样本挖掘损失来减少采样消耗并加快收敛速度。这两项修改使得所提出的模型能够实现 SOTA 性能，同时速度是其他 EA 方法的数倍。主要实验表明，我们的方法在所有数据集和指标上都优于竞争对手。此外，我们设计了辅助实验来证明每个组件的有效性和模型的可解释性。

论文地址：

https://arxiv.org/pdf/2103.15452.pdf

代码：

关系，而且还大大降低了计算复杂度。为了取代低效的采样策略，我们提出归一化硬样本挖掘损失来减少采样消耗并加快收敛速度。这两项修改使得所提出的模型能够实现 SOTA 性能，同时速度是其他 EA 方法的数倍。主要实验表明，我们的方法在所有数据集和指标上都优于竞争对手。此外，我们设计了辅助实验来证明每个组件的有效性和模型的可解释性。

论文地址：

https://arxiv.org/pdf/2103.15452.pdf

代码：

https://github.com/MaoXinn/Dual-AMN