前言

算法对于我们普通的工程师来说可算得上陌生又熟悉，因为在平时的业务代码中可能见到他的身影比较少，但在底层的代码中我们可能会经常发现排序算法的影子，如数据库索引，操作系统的进程调度。因此，掌握这种算法中的思想还是致关重要，今天大猿就带大家来实战一下基础的排序算法，加强记忆。

常见的排序分类

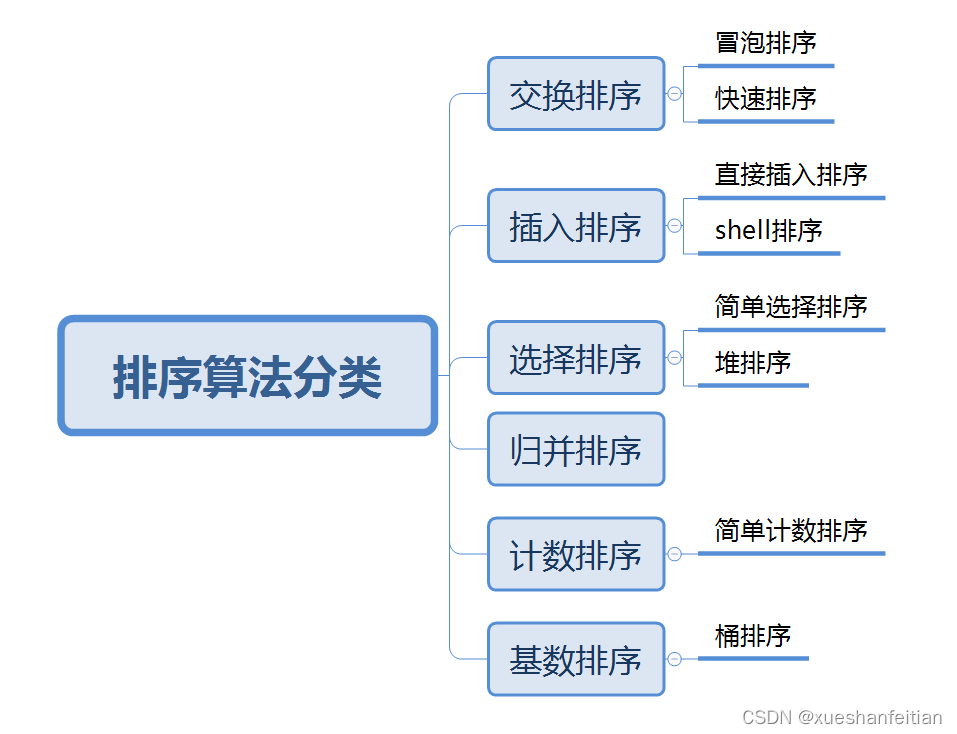
直接插入排序

先直接上代码:

    public static void insertSort2(int [] arr){for (int i = 1; i < arr.length; i++) {int key = arr[i];int j=i-1;for ( ; j >= 0 ; j--) {if(key < arr[j]){arr[j + 1] = arr[j];}else {break;}}arr[j + 1] = key;}StringBuffer stringBuffer = new StringBuffer();for (int j : arr) {stringBuffer.append(",").append(j);}System.out.println(stringBuffer);}public static void main(String[] args) {int [] arr = {345,23,79,54,67,666,23,78,2,22,985};//   insertSort(arr);insertSort2(arr);}

运行结果

复杂度

时间复杂度

运行复杂度，当整个序列基本有序的情况下此时插入排序将出现最好情况 O(n) , 这个也不难想象，当整个排序序列基本有效时，比较只需要n次，内部循环几乎可以不执行。
对于一般情况时间复杂度是O(n^2);

空间复杂度

因为在程序执行过程中，我们只用一个一个临时存储变量，所以空间复杂度为O(1);

稳定性

该算法是稳定算法，如何理解稳定性呢？稳定性最直白的理解就是如果出现相同元素的时候，看原来的序列是否遭到破坏。

希尔排序

上代码，

    public static void main(String[] args) {int[] arr = new int[100];for (int i = 0; i < 100; i++) {arr[i] = (int) (Math.random() *100);}shellSort(arr);}public static void shellSort(int [] arr){for (int gap = arr.length /2; gap>0; gap /=2){for(int i = gap; i < arr.length ; i ++){int temp = arr[i];int j=i - gap;for( ; j >= 0; j -= gap){if(arr[j] < temp){arr[j+gap]=arr[j];}else {break;}}arr[j+gap] = temp;}}StringBuffer stringBuffer = new StringBuffer();for (int j : arr) {stringBuffer.append(",").append(j);}System.out.println(stringBuffer);}

运行结果

复杂度

时间复杂度

希尔排序可以理解为特殊的插入排序，最好和最坏时间复杂度基本与插入排序保持一致。软设上给出的平均复杂度为O(n^1.3) 有兴趣的同学可以去研究一下理论。

空间复杂度

空间复杂度基本与插入排序是一致的。

稳定性

该算法为非稳定算法。

计数排序

代码

    public static int[] countSort(int[] array) {//1.得到数列的最大值int max = array[0];for(int i=1; i<array.length; i++){if(array[i] > max){max = array[i];}}//2.根据数列最大值确定统计数组的长度int[] countArray = new int[max+1];//3.遍历数列，填充统计数组for(int i=0; i<array.length; i++){countArray[array[i]]++;}//4.遍历统计数组，输出结果int index = 0;int[] sortedArray = new int[array.length];for(int i=0; i<countArray.length; i++){for(int j=0; j<countArray[i]; j++){sortedArray[index++] = i;}}return sortedArray;}public static int[] countSortV2(int[] array) {//1.得到数列的最大值和最小值，并算出差值dint max = array[0];int min = array[0];for(int i=1; i<array.length; i++) {if(array[i] > max) {max = array[i];}if(array[i] < min) {min = array[i];}}int d = max - min;//2.创建统计数组并统计对应元素个数int[] countArray = new int[d+1];for(int i=0; i<array.length; i++) {countArray[array[i]-min]++;}//3.统计数组做变形，后面的元素等于前面的元素之和for(int i=1;i<countArray.length;i++) {countArray[i] += countArray[i-1];}//4.倒序遍历原始数列，从统计数组找到正确位置，输出到结果数组int[] sortedArray = new int[array.length];for(int i=array.length-1;i>=0;i--) {sortedArray[countArray[array[i]-min]-1]=array[i];countArray[array[i]-min]--;}return sortedArray;}public static void main(String[] args) {int[] array = new int[] {4,4,6,5,3,2,8,1,7,5,6,0,10};int[] sortedArray = countSort(array);System.out.println(Arrays.toString(sortedArray));array = new int[] {95,94,91,98,99,90,99,93,91,92};sortedArray = countSortV2(array);System.out.println(Arrays.toString(sortedArray));}

运行结果

时间复杂度

计数排序的时间复杂度为O(n+k)，其中n是待排序序列的长度，k是待排序序列中的最大值，注意计算时间复杂度时只是考虑了构造统计数组的最大长度k和

空间复杂度

计数排序的空间复杂度为O(k)。

稳定性

该算法是一个稳定算法，对于数的范围不大，但是算量很多的情况非常实用。

选择排序

继续先上代码

    public static void selectSort(int [] arr){int maxIndex =0;for (int i = 0; i < arr.length-1; i++) {for (int j = i; j <arr.length ; j++) {if(arr[maxIndex]<arr[j]){maxIndex =j;}}if(maxIndex != i){int temp =0;temp = arr[maxIndex];arr[maxIndex] = arr[i];arr[i] = temp;}}StringBuffer stringBuffer = new StringBuffer();for (int i = 0; i <arr.length; i++) {stringBuffer.append(",").append(arr[i]);}System.out.println(stringBuffer.toString());}public static void main(String[] args) {int [] arr = {345,23,79,54,67,666,23,78,2,22,985};selectSort(arr);}

运行结果

时间和空间复杂度

选择排序的时间复杂度为O(n^2) 空间复杂度为O(1)

稳定性

该算法为不稳定算法。

堆排序

堆排序稍微复杂点，先上个截图，至于具体理论的话请同学们自己去找教材或者视频，下面给出算法及代码

    public static void main(String[] args) {int arr [] ={1,10,3,2,6,5,7,9,8,0,4};heapSort(arr);System.out.println(Arrays.toString(arr));}/**** @param array*/private static  void heapSort(int []  array){//构建堆for (int i = (array.length-2)/2; i >=0; i--) {downAdjust(array,i,array.length);}System.out.println("-----------------------");System.out.println(Arrays.toString(array));//调整堆for (int i = array.length-1; i >0; i--) {int temp = array[i];array[i] = array[0];array[0] = temp;downAdjust(array,0,i);/*            if("UP".equals(cmd)){upAdjust(array);}*/}}/**** 节点下沉* @param arr* @param parentIndex* @param length*/private static void  downAdjust(int [] arr,int parentIndex , int length){int temp = arr[parentIndex];int childIndex = 2* parentIndex +1;while (childIndex < length){//定位到右孩子if(childIndex+1 < length && arr[childIndex+1]>arr[childIndex]){childIndex++;}if(temp > arr[childIndex]){break;}arr[parentIndex] = arr[childIndex];parentIndex = childIndex;childIndex = 2* childIndex+1;}arr[parentIndex] = temp;// System.out.println(Arrays.toString(arr));}

运行结果

复杂度及稳定性

堆排序是不稳定排序，其时间复杂度时O(nlog(2)n),空间复杂度为n+1；此外
该算法是非稳定算法。

冒泡排序

代码如下：

    public static void main(String[] args) {int [] arr = {345,23,79,54,67,666,23,78,2,22,985};bubbleSort(arr);}public static void  bubbleSort(int [] arr){for (int i = 0; i < arr.length; i++) {for (int j = 0; j < arr.length - i - 1; j++) {int temp = 0;if (arr[j] < arr[j+1]) {temp = arr[j];arr[j]=arr[j+1];arr[j+1] = temp;}}}StringBuffer stringBuffer = new StringBuffer();for (int i = 0; i <arr.length; i++) {stringBuffer.append(",").append(arr[i]);}System.out.println(stringBuffer.toString());}

运行结果

复杂度分析及稳定性分析

冒泡算法的复杂度为O(n^2) 空间复杂度为O(1)，该算法为稳定的排序算法。

快速排序

主算法

    public static void main(String[] args) {int [] arr = {345,23,79,54,67,666,23,78,2,22,985};quickSort(arr,0,arr.length-1);StringBuffer stringBuffer = new StringBuffer();for (int i = 0; i <arr.length; i++) {stringBuffer.append(",").append(arr[i]);}System.out.println(stringBuffer.toString());}public static void quickSort(int [] arr, int start,int end){if(start > end){return;}int midIndex = partition(arr, start, end);quickSort(arr,start,midIndex-1);quickSort(arr,midIndex+1,end);}private static int partition(int[] arr, int start, int end) {int right = end;int left = start;int midValue = arr[left];while (left != right){while (left<right && midValue < arr[right]){right --;}// arr[left] = arr[right];while (left<right && midValue >= arr[left]){left ++;}//  arr[right] = arr[left];if(left < right){int temp =0;temp = arr[left];arr[left] = arr[right];arr[right] = temp;}}arr[start] = arr[right];arr[right] = midValue;return right;}

运行结果

复杂度分析

时间复杂度

快速排序的一般时间复杂度为 O(nlog(2)n) ,最坏的时间复杂度为O(n^2);

空间复杂度

递归算法的空间复杂度 = 每次递归的空间复杂度O(1) * 递归深度， 因为堆栈的深度就是快速排序的空间复杂度位O(log(2)n)，最坏也就是O(n)

稳定性

快速排序为不稳定算法

归并排序

先上代码

    public static void main(String[] args) {int [] arr = {345,23,79,54,67,666,23,78,2,22,985};mergeSort(arr, 0, arr.length - 1);for (int i : arr) {System.out.print(i + " ");}}public static void mergeSort(int[] arr, int left, int right) {if (left < right) {int mid = (left + right) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);}}public static void merge(int[] arr, int left, int mid, int right) {int[] temp = new int[right - left + 1];int i = left;int j = mid + 1;int k = 0;while (i <= mid && j <= right) {if (arr[i] <= arr[j]) {temp[k++] = arr[i++];} else {temp[k++] = arr[j++];}}while (i <= mid) {temp[k++] = arr[i++];}while (j <= right) {temp[k++] = arr[j++];}for (int p = 0; p < temp.length; p++) {arr[left + p] = temp[p];}}

运行结果

时间复杂度

从上面的代码来看，其归并的深度为log(2)n 而每次合并的时间复杂度都为n，所以综合下来其时间复杂度为 n*log(2)n;

空间复杂度

因为归并需要额外的空间数组，其大小n

稳定性

该算法为稳定的排序算法，相同元素不改变原来的位置。

桶排序

桶排序的基本思想可以说是与计数排序有异曲同工之妙，由于篇幅原因，需要了解算法的具体实现的小伙伴可以自己去翻阅资料。

总结

• 本文带大家实战了常见的排序算法，并给出了运行结果，其中采用 动态规划 思想的算法有 选择排序 ; 选择排序、冒泡排序和堆排序 都属于 贪心法，而 归并排序 采用了分治思想；希尔排序可以说是既采用了动态规划思想，又采用了分之思想；快速排序既采用贪心算法，又吸收了分治思想 。
• 对于不同场景我们可以采用不同的排序算法，从时间复杂度来看，快排，归并，堆排序是响应速度最快的三种常见排序方法，但所占空间都比较高；从空间复杂度来看，冒泡，插入，简单选择排序是应用空间最小的排序方法，但响应时间有点慢；复杂为线性的排序算法只有基数排序和桶排序，但该算法并不适合所有的应用场景，所以在实际应用大各位小伙伴要懂得权衡利弊，妥善处置。