算法学习笔记Day9——动态规划基础篇

一、介绍

本文解决几个问题：动态规划是什么？解决动态规划问题有什么技巧？如何学习动态规划？

1. 动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。

2. 动态规划的核心思想就是穷举求最值，但只有列出正确的「状态转移方程」，才能正确地穷举。你需要判断算法问题是否具备「最优子结构」，是否能够通过子问题的最值得到原问题的最值。另外，动态规划问题存在「重叠子问题」，如果暴力穷举的话效率会很低，所以需要你使用「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。

3. 思维框架：明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。

递归是自顶向下，动态规划是自底向上

4. 带备忘录的递归和动态规划实际上是等价的，动态规划是从底层开始，一步一步完成对数组的完善，所以不需要备忘录，或者说dp数组本身就是备忘录，递归会遇到很多重复的子问题，所以需要备忘录来简化。

二、例题

例题1：斐波那契数

分析：

写出状态转移方程，写出基底，就可以开始自底向上构造了。

代码：

思路1：自底向上解法

class Solution {
public:int fib(int n) {if(n == 0 || n == 1){return n;}int fib_1 = 1, fib_2 = 0;int fib_i;for(int i = 2; i<= n; i++){fib_i = fib_1 + fib_2;fib_2 = fib_1;fib_1 = fib_i;}return fib_i;}
};

思路2：自顶向下解法

class Solution {
public:vector<int> diary;int recursion(int n){//基地if(n == 0 || n == 1){return n;}//查日记if(diary[n] != -1){return diary[n];}//日记没查到，更新日记，用递归更新它diary[n] = recursion(n-1) + recursion(n-2);//再查找日记本return diary[n];}int fib(int n) {diary.resize(n+1, -1);return recursion(n);}
};

例题2：零钱兑换

分析：

写出状态方程就可以了

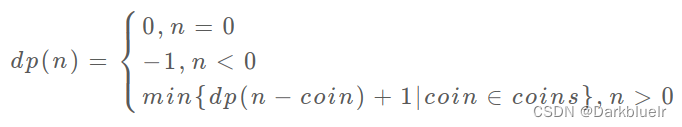
代码：

思路1：带备忘录的递归

class Solution {
public:vector<int> diary;int dp(vector<int>& coins, int amount){if(amount < 0){return -1;}if(amount == 0){return 0;}if(diary[amount] != 0){return diary[amount];}int ans = INT_MAX;for(int coin : coins){int subsolution = dp(coins, amount - coin);if(subsolution != -1){ans = min(subsolution+1, ans);}}diary[amount] = ans==INT_MAX ? -1:ans;return diary[amount];}int coinChange(vector<int>& coins, int amount) {diary.resize(amount+1, 0);return dp(coins, amount);}
};

不知道为什么把diary初始化为-1就会超时，推测是-1表示不可能的情况，有很多正数diary也是-1，就容易进入循环，但是0只有0这个情况。

思路2：dp迭代

class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX-1);//base situationdp[0] = 0;for(int i  =0; i<=amount; i++){for(int coin : coins){if(i - coin < 0){continue;}dp[i] = min(dp[i], dp[i-coin] + 1);}}return dp[amount]==INT_MAX-1?-1:dp[amount];}
};

例题3：最长递增子序列

分析：

首先要明确dp数组代表什么，这里是以位置i数字结尾的最长字序列长度，对于每个位置，比较前面的位置，只要它大于某个元素，就可以和那个元素的最长子序列组成新的最长子序列。

代码：

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);for(int i  = 0; i< nums.size(); i++){for(int j = 0; j<i; j++){if(nums[i] > nums[j])dp[i] = max(dp[i], dp[j] + 1);}}return *max_element(dp.begin(), dp.end());}
};

例题4：俄罗斯套娃信封问题

代码：

class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {int n = envelopes.size();sort(envelopes.begin(), envelopes.end(), [](vector<int>& a, vector<int>& b)->bool{return a[0] == b[0]? a[1] > b[1] : a[0] < b[0];});vector<int> dp(n, 1);for(int i = 0; i<n; i++){for(int j = 0; j< i; j++){if(envelopes[i][1] > envelopes[j][1]){dp[i] = max(dp[i], dp[j] + 1);}}}return *max_element(dp.begin(), dp.end());}
};