在深度学习领域，激活函数是神经网络中的关键组成部分，它决定了网络的输出和性能。近年来，研究人员提出了许多新的激活函数，其中Swish激活函数因其独特的性能优势而备受关注。这种函数在2017年被重新发现，并被认为是Swish函数的一个变体。Swish函数不仅性能卓越，还能有效缓解梯度消失问题，因此在神经网络中得到了广泛应用。

Swish激活函数

Swish激活函数的数学定义如下：

$$\text{Swish}\left(x\right)=x\sigma \left(\beta x\right)$$

其中，$\sigma$ 是Sigmoid函数，$\beta$ 是一个可学习的参数

• 当$\beta =1$时，该函数简化为$\text{Swish}(x)=x\sigma (x)$， 这与2016年首次提出的Sigmoid线性单元（SiLU）等价。SiLU后来在2017年被重新发现，作为强化学习中的Sigmoid加权线性单元（SiL）函数。SiLU/SiL在被最初发现一年多后再次被重新发现为Swish函数，最初提出时没有可学习的参数$\beta$，因此β隐式等于1。然后，Swish论文被更新，提出了带有可学习参数β的激活函数，尽管研究人员通常让$\beta =1$，并不使用可学习的参数β。

• 对于$\beta =0$，该函数变为缩放线性函数$f(x)=x/2$。

• 当$\beta \to \infty$时，sigmoid组件趋向于点对点的0-1函数，因此swish函数点对点趋向于ReLU函数。因此，它可以被视为一个平滑函数，它非线性地在线性函数和ReLU函数之间插值。这个函数利用了非单调性，并且可能影响了具有这种特性的其他激活函数的提出，例如Mish。

当考虑正值时，Swish是Sigmoid收缩函数的特殊情况。

2017年，在对ImageNet数据集进行分析后，谷歌的研究人员发现，将Swish函数作为人工神经网络的激活函数，可以提高模型的性能，相较于ReLU和sigmoid函数。人们认为，性能提升的一个原因是Swish函数有助于在反向传播过程中缓解梯度消失问题。

---

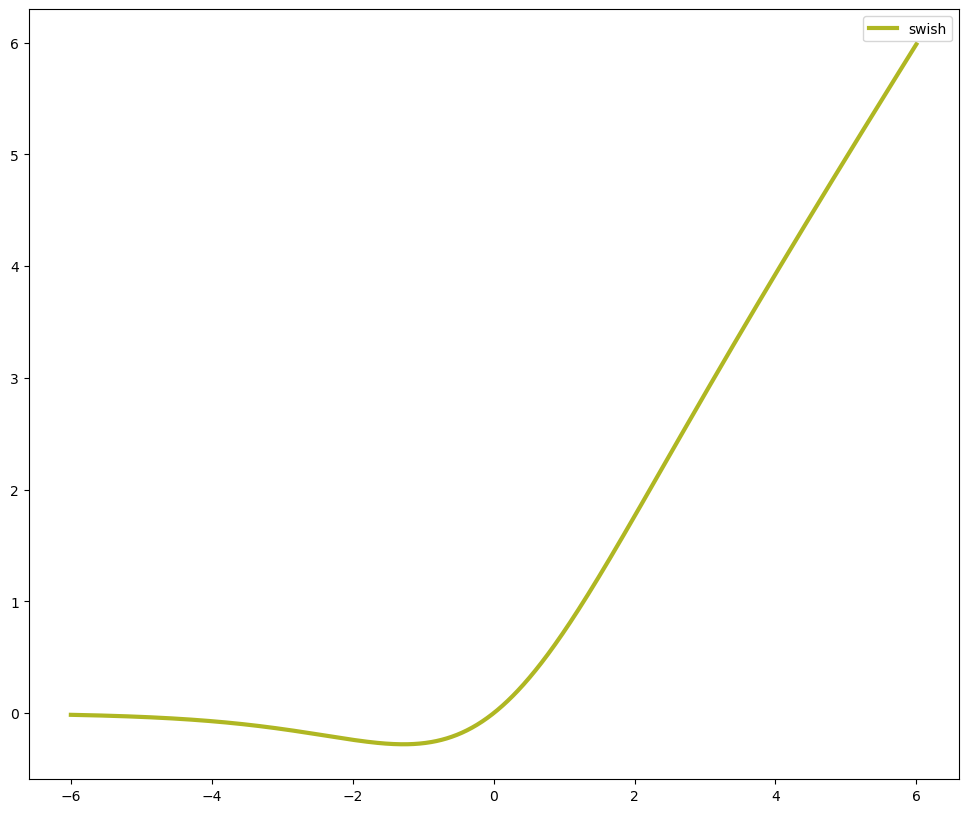
Swish函数的性能优势主要体现在以下几个方面：

1. 缓解梯度消失问题：Swish函数在正向传播过程中能够产生较大的梯度，有助于缓解梯度消失问题，从而提高模型的训练效率。
2. 非单调性：Swish函数具有非单调性，这意味着它在某些区间内能够提升模型的表达能力，有助于提高模型的性能。
3. 平滑性：Swish函数在输入值较大时接近线性函数，这使得它在神经网络中能够平滑地插值于线性函数和ReLU函数之间，从而提高模型的泛化能力。

Swish函数在反向传播中的作用：

在反向传播过程中，Swish函数的导数 $\frac{\partial \text{Swish}(x)}{\partial x}$ 为 $\text{Swish}(x)\cdot {\sigma }^{\prime }(\beta x)$，其中 ${\sigma }^{\prime }$ 是Sigmoid函数的导数。这个导数在 $\beta$ 的影响下，能够保持较大的值，从而有助于提高模型的训练效率。

H-Swish激活函数

Hard Swish是Swish的一个变体，它被开发出来以简化公式的计算。原始的Swish公式包括Sigmoid函数，这在计算上相对昂贵。Hard Swish用一个分段线性函数替换Sigmoid函数，这使得计算变得更加简单。

$$\text{h-swish}\left(x\right)=x\frac{\text{ReLU6}\left(x+3\right)}{6}$$

在上述公式中，x是激活函数的输入值，而ReLU6是Rectified Linear Unit（ReLU）函数的一个变体。

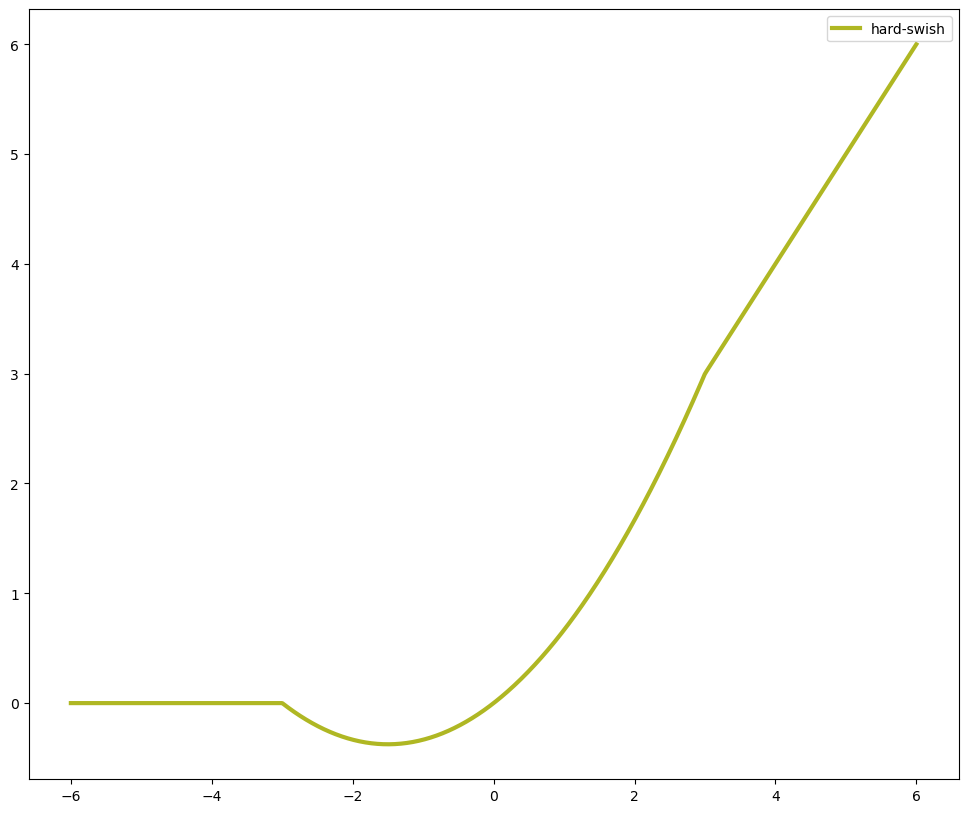
H-Swish相对于原始Swish的优势主要包括：

1. 计算效率：H-Swish使用分段线性函数替换了Sigmoid函数，这使得计算变得更加简单，降低了计算成本。
2. 易于集成：H-Swish易于集成到现有的机器学习应用中，无需对算法架构进行重大更改，使得开发人员能够快速采用。
3. 性能保持：尽管H-Swish简化了计算过程，但它仍然保持了与原始Swish类似的性能优势，如缓解梯度消失问题和非单调性。

通过这些优势，H-Swish成为了一个优化的激活函数选择，特别是在需要高效计算和快速模型训练的场景中。

实现

在下面的代码示例中，将使用Numpy库来实现Swish、H-Swish以及其他相关函数，并绘制它们的图形表示。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error# define cost functions
def mish(x):return x * np.tanh(np.log(1+np.exp(x)))def swish(x):return (x*np.exp(x))/(np.exp(x)+1)def relu(x):return np.maximum(x,0)def hard_swish(x, a_max=6, amin=0, add=3, divide=6):return x*np.clip(x+add, a_min=amin, a_max=a_max)/divide# Plot
x = np.linspace(-6, 6, num=1000)
y_mish = mish(x)
y_swish = swish(x)
y_hard_swish = hard_swish(x)
fig,ax = plt.subplots(1, 1, figsize=(12,10))
ax.plot(x, y_mish, label='mish', lw=3,color='#b5002e')
ax.plot(x, y_swish, label='swish', lw=3, color='#001b6e')
ax.plot(x, y_hard_swish, label='hard-swish', lw=3, color='#afb723')
ax.legend()

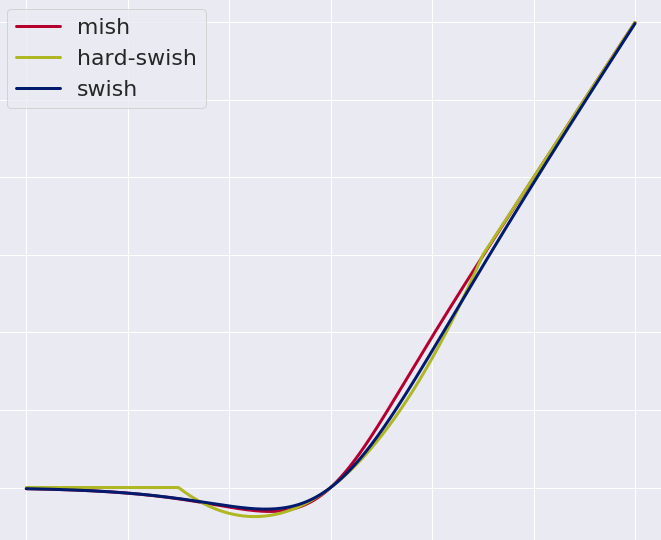
这段代码定义了Swish、H-Swish、ReLU6函数，并使用Matplotlib库绘制了它们的图形表示。通过观察这些图形，可以直观地看到这些激活函数的特性，如Swish和H-Swish的平滑性等。

总结

Swish和H-Swish激活函数在深度学习领域的重要性不容忽视。它们不仅提供了优异的性能，还在神经网络的训练过程中发挥着关键作用。

Swish激活函数因其能够有效缓解梯度消失问题而受到重视。这种函数的非单调性和平滑性使其在模型训练中能够更好地表达复杂的函数关系，从而提高模型的泛化能力。此外，Swish函数的简单性和高效性也使其在实际应用中得到了广泛的应用。

H-Swish激活函数则是在Swish的基础上进一步优化的结果。它通过使用分段线性函数替代Sigmoid函数，大大提高了计算效率，使得模型训练更加快速。同时，H-Swish保持了与Swish类似的性能优势，使得它成为了一种既高效又有效的激活函数选择。

总的来说，Swish和H-Swish激活函数在神经网络中的应用为深度学习的发展提供了新的思路和可能性。它们的出现不仅丰富了激活函数家族，也为模型训练的效率和性能提升提供了新的可能。随着研究的不断深入，可以期待这些激活函数在未来发挥更大的作用，推动深度学习技术的发展。

参考

• Ramachandran, Prajit; Zoph, Barret; Le, Quoc V. “Searching for Activation Functions”
• Hendrycks, Dan; Gimpel, Kevin. “Gaussian Error Linear Units (GELUs)”
• Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji . “Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning”
• Misra, Diganta (2019). “Mish: A Self Regularized Non-Monotonic Neural Activation Function”.
• Atto, Abdourrahmane M.; Pastor, Dominique; Mercier, Gregoire. “Smooth sigmoid wavelet shrinkage for non-parametric estimation”
• Serengil, Sefik Ilkin. “Swish as Neural Networks Activation Function”
• https://serp.ai/hard-swish/