点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励，我们一起努力吧!😃😃

1.有效三角形的个数

题目链接：633.有效三角形的个数

题目描述：

一般三角形我们判断方法是任意两边之和大于第三边

算法原理:

解法一: 暴力求解

选三个数进行判断，一般我们一定会想到三层for循环进行判断，下面是伪代码，时间复杂度O(N^3)

解法二：利用单调性，使用双指针算法来解决问题

任意两边之和大于第三边，三个数需要判断三次
a+b>c
a+c>b
b+c>a

现在a、b、c三个数，先对它们进行排序，a<=b<=c;
a+b>c
a+c>b
b+c>a
我们只需要判断一次 a+b>c就也把下面两次判断包括了。因为c是最大的！

注意这只是固定了10一次循环，还要在从后往前固定

1. 先固定最大的数
2. 在最大数的左区间内，使用双指针算法，快速统计符合要求的三元组个数

class Solution {
public:int triangleNumber(vector<int>& nums) {  //1.优化sort(nums.begin(),nums.end());//2.利用双指针快速解决问题int sum=0;for(int i=nums.size()-1;i>=2;--i)//先固定最大数{//利用双指针快速统计符合要求的三元组个数int left=0,right=i-1;while(left<right){if(nums[left]+nums[right]>nums[i]){sum+=(right-left);--right;}else{++left;}}}return sum;}
};

总结：有些题可以进行排序或者已经排好了序，然后利用单调性，使用双指针算法解决问题，双指针一个指向最小值，一个指向最大值，然后根据题意利用单调性一次排除一批。

2.和为S的两个数字

题目链接：JZ57 和为S的两个数字

题目描述：

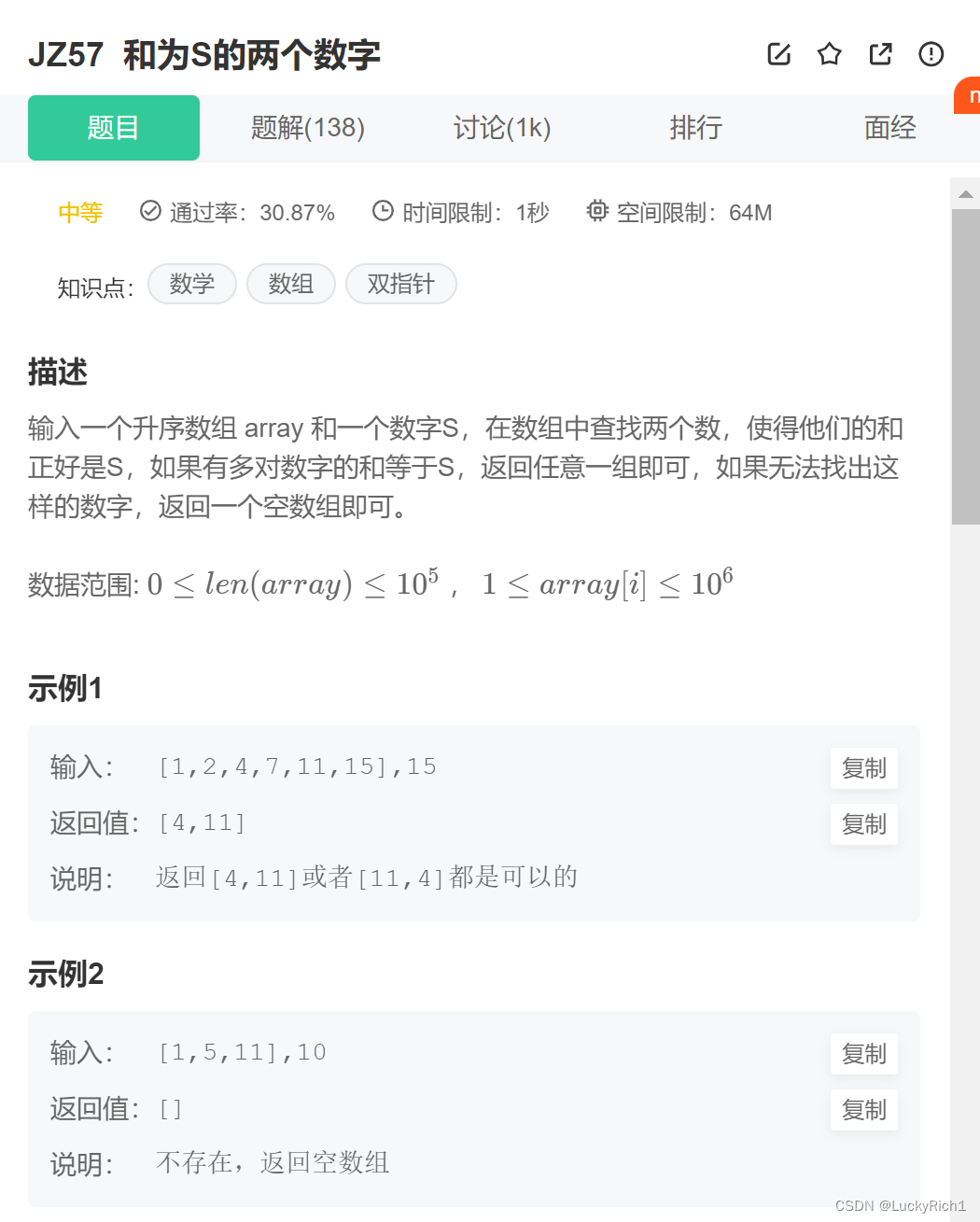
算法原理：

解法一：暴力枚举求解O(N^2)
拿到题我们马上就会想到暴力求解，两层for循环，以下是伪代码

解法2：使用单调性，使用双指针算法解决问题
本题排好序了，我们直接使用双指针即可，一个指向最左边，一个指向最右边。然后根据条件利用单调性一次排除一批。O(N)

class Solution {
public:vector<int> FindNumbersWithSum(vector<int> array,int sum) {int left=0,right=array.size()-1,ret=0;while(left<right){ret=array[left]+array[right];if(ret>sum) --right;else if(ret<sum) ++left;else return {array[left],array[right]};}return {};}
};

3. 三数之和

题目链接：15. 三数之和

题目描述：

题目分析：

这道题我们根据它的用例来分析，要找下标不同的数，使其相加和为0。下面虽然有三组解，下标也不同，但是第一组和第三组它们的数是相同的，因此只能去重留下一组。

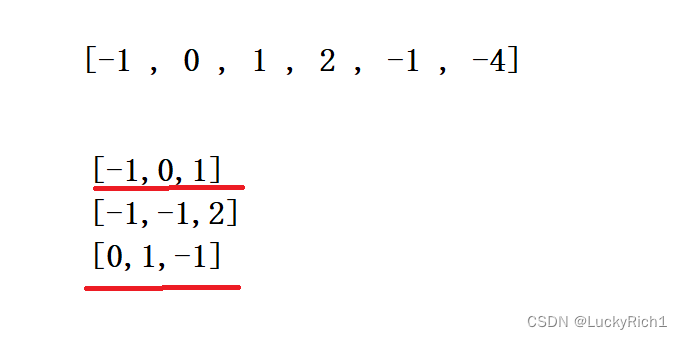
算法原理：

一般这里我们还是首先会想到暴力求解，这是没问题的，因为我们的优化就是从暴力求解上来的。

对于这道题，它要最后把结果还要去重，我们一般考虑得到结果然后每个排序之后在去重。其实我们可以先排序。然后在去重，去重我们有容器set和unordered_set，因此第一种解法出来了。

解法一：排序+暴力枚举+利用set去重

解法二：排序之后，使用单调性，使用双指针算法解决问题

本题是找三元组，因此我们排好序之后，固定一个数，然后利用双指针求解。所以以后遇到三元组的问题可以采用这种方法

1. 排序
2. 固定一个数a
3. 在该数后面的区间内，利用 “双指针算法” 快速找到两个的和等于-a即可

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {//1.排序sort(nums.begin(),nums.end());vector<vector<int>> vc;//2.利用双指针解决问题for(int i=0;i<nums.size()-2;++i)//固定a{if(nums[i]>0)//小优化break;int left=i+1,right=nums.size()-1,target=-nums[i];while(left<right){int sum=nums[left]+nums[right];if(sum>target) --right;else if(sum<target) ++left;else{vc.push_back({nums[i],nums[left],nums[right]});//不漏++left,--right;//去重left,rightwhile(left < right && nums[left] == nums[left-1]) ++left;while(left < right && nums[right] == nums[right+1]) --right;}}//去重iwhile(i < nums.size()-2 && nums[i] == nums[i+1]) ++i;}return vc;        }
};

4.四数之和

题目链接：18.四数之和

题目描述：

这道题和上面三数之和几乎一模一样

算法原理:

解法一：排序+暴力枚举+容器set去重
时间复杂度O(N^4)

解法二：排序+双指针

1. 依次固定一个数 a
2. 在 a 后面的区间内，利用 “三数之和” 找到三个数，是这三个数字的和等于 target - a 即可

三数之和

1. 依次固定一个数 b
2. 在 b 后面的区间内，利用 “双指针” 找到两个数，使这两个数的和等于 target - a - b 即可

处理细节问题：

1. 去重
2. 不漏
   

class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {//1.排序sort(nums.begin(),nums.end());//2.利用双指针解决问题vector<vector<int>> ret;int n=nums.size();for(int i=0;i<n-3;++i)//固定数 a{//利用 三数之和for(int j=i+1;j<n-2;++j) //固定数 b{//双指针int left=j+1,right=n-1;int aim=target-nums[i]-nums[j];while(left<right){int sum=nums[left]+nums[right];if(sum>aim) --right;else if(sum<aim) ++left;else{ret.push_back({nums[i],nums[j],nums[left],nums[right]});//不漏++left;--right;//去重1while(left<right && nums[left] == nums[left-1]) ++left;while(left<right && nums[right] == nums[right+1]) --right;}}//去重2while(j+1 < n-2 && nums[j+1] == nums[j]) ++j;}//去重3while(i+1 < n-3 && nums[i+1] == nums[i]) ++i;}return ret;}
};

注意这里会有数据溢出的问题。

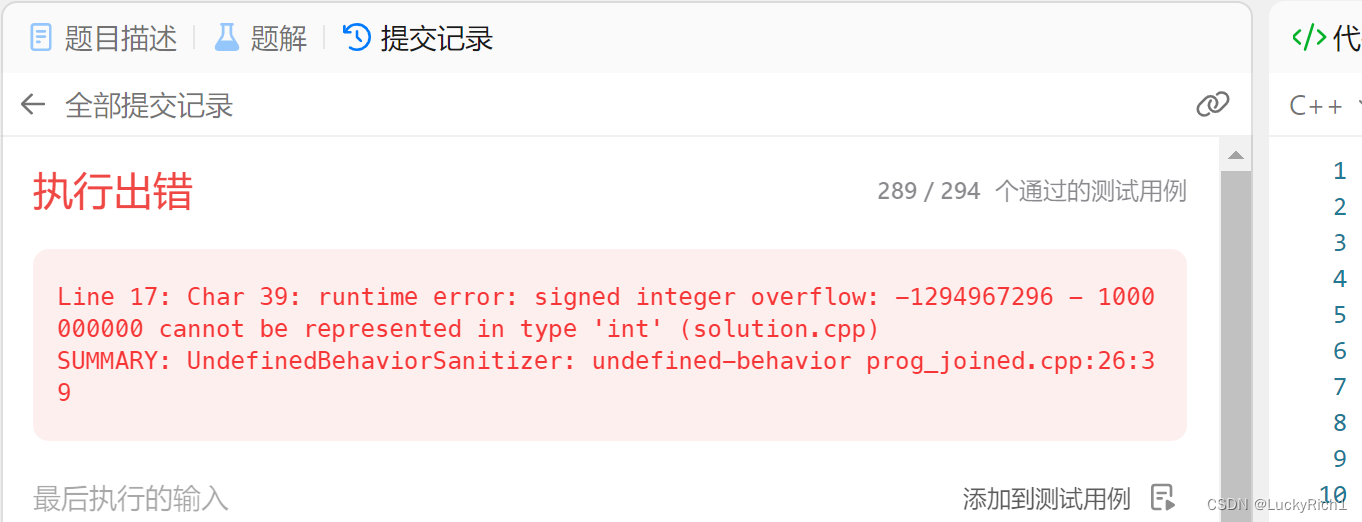
因此两数相减的时候，使用long long

class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {//1.排序sort(nums.begin(),nums.end());//2.利用双指针解决问题vector<vector<int>> ret;int n=nums.size();for(int i=0;i<n-3;++i)//固定数 a{//利用 三数之和for(int j=i+1;j<n-2;++j) //固定数 b{//双指针int left=j+1,right=n-1;long long aim=(long long)target-nums[i]-nums[j];while(left<right){int sum=nums[left]+nums[right];if(sum>aim) --right;else if(sum<aim) ++left;else{ret.push_back({nums[i],nums[j],nums[left],nums[right]});//不漏++left;--right;//去重1while(left<right && nums[left] == nums[left-1]) ++left;while(left<right && nums[right] == nums[right+1]) --right;}}//去重2while(j+1 < n-2 && nums[j+1] == nums[j]) ++j;}//去重3while(i+1 < n-3 && nums[i+1] == nums[i]) ++i;}return ret;}
};