笔记：编写程序，分别采用面向对象和 pyplot 快捷函数的方式绘制正弦曲线和余弦曲线。提示：使用 sin()或 cos()函数生成正弦值或余弦值。

文章目录

前言
一、面向对象和 pyplot 快捷函数的方式是什么？
二、编写代码
- 面向对象的方法：
- 使用 pyplot 快捷函数的方法：
总结

前言

本文将探讨如何使用编程语言编写程序，通过两种不同的方法绘制正弦曲线和余弦曲线。我们将分别采用面向对象的编程范式和 pyplot 快捷函数来实现这一目标。

在科学计算和数据可视化领域，绘制正弦曲线和余弦曲线是一项常见的任务。这两种曲线在描述周期性现象和波动性数据方面具有广泛的应用。通过学习如何使用编程工具绘制这些曲线，我们不仅可以更好地理解它们的数学特性，还能够在实际工作中利用这些技能进行数据分析和可视化。

在本文中，我们将首先介绍面向对象编程范式，然后探讨使用 pyplot 快捷函数的方法。通过比较这两种方法的优缺点，读者将更好地理解如何选择适当的工具来解决特定的绘图任务。

在开始编写具体的代码之前，让我们先了解一下正弦曲线和余弦曲线的基本概念，以便更好地理解我们将要实现的程序。正弦曲线和余弦曲线是周期性的函数，它们描述了随时间或空间变化而周期性波动的现象。正弦曲线表示一种连续的周期性波动，而余弦曲线则是正弦曲线的相位延迟90度的变体。

一、面向对象和 pyplot 快捷函数的方式是什么？

面向对象编程（Object-Oriented Programming，OOP）是一种编程范式，它将程序设计构建为一组对象的集合，这些对象可以通过消息传递来交互。在绘制正弦曲线和余弦曲线时，面向对象的方式通常涉及创建一个包含曲线数据和绘制方法的类，并在需要时实例化该类对象并调用其方法来进行绘制。

而 pyplot 快捷函数则是 matplotlib 库提供的一种方便快捷的绘图方式。Matplotlib 是一个 Python 的绘图库，pyplot 是其面向过程的界面，提供了许多函数来快速绘制各种类型的图形，包括正弦曲线和余弦曲线。使用 pyplot 快捷函数，你可以直接调用一系列函数来生成并显示图形，而无需显式地创建类或对象。

下面是分别使用面向对象和 pyplot 快捷函数的方式绘制正弦曲线和余弦曲线的简要说明：

面向对象方式：
- 创建一个包含绘制曲线方法的类，该方法接受正弦或余弦函数的参数，并使用 matplotlib 库来绘制曲线。
- 实例化该类对象，并调用其绘制方法来生成相应的图形。
pyplot 快捷函数方式：
- 导入 matplotlib.pyplot 模块，该模块提供了一组快速绘图的函数。
- 直接调用 pyplot 模块中的函数，比如 plt.plot() 来生成正弦曲线和余弦曲线的图形。

下面将提供两种方式的代码示例来说明具体的实现方法。

二、编写代码

面向对象的方法：

# 首先是面向对象的方法：
# 导入 NumPy 和 Matplotlib 库
import numpy as np
import matplotlib.pyplot as plt# 定义一个函数来绘制正弦和余弦曲线
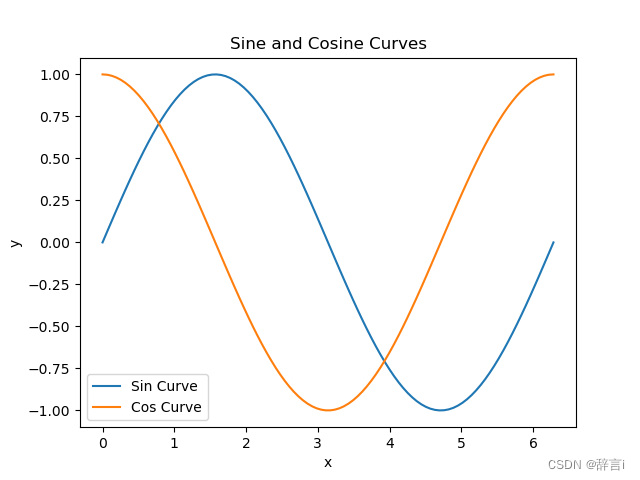
def plot_sin_cos(x):# 计算正弦和余弦函数在给定 x 值处的值y_sin = np.sin(x)y_cos = np.cos(x)# 使用 Matplotlib 绘制正弦和余弦曲线plt.plot(x, y_sin, label='Sin Curve')  # 绘制正弦曲线plt.plot(x, y_cos, label='Cos Curve')  # 绘制余弦曲线# 添加 x 轴和 y 轴标签plt.xlabel('x')plt.ylabel('y')# 添加标题plt.title('Sine and Cosine Curves')# 添加图例plt.legend()# 显示图形plt.show()# 生成 x 值，在 0 到 2π 之间生成 100 个等间隔的点
x = np.linspace(0, 2 * np.pi, 100)# 调用函数来绘制正弦和余弦曲线
plot_sin_cos(x)

这段代码使用了NumPy和Matplotlib库来生成并绘制正弦和余弦曲线。让我逐行解释：

import numpy as np: 导入NumPy库并使用别名np。
import matplotlib.pyplot as plt: 导入Matplotlib库中的绘图模块，并使用别名plt。
def plot_sin_cos(x): 定义了一个名为plot_sin_cos的函数，它接受一个参数x，用于绘制正弦和余弦曲线。
y_sin = np.sin(x)和y_cos = np.cos(x): 计算给定x值处的正弦和余弦函数值。
plt.plot(x, y_sin, label='Sin Curve')和plt.plot(x, y_cos, label='Cos Curve'): 使用Matplotlib的plot函数绘制正弦曲线和余弦曲线，并给曲线添加标签。
plt.xlabel('x')和plt.ylabel('y'): 添加x轴和y轴的标签。
plt.title('Sine and Cosine Curves'): 添加图表的标题。
plt.legend(): 添加图例，显示每条曲线对应的标签。
plt.show(): 显示绘制的图形。

然后，代码生成了一个包含100个等间隔点的x值数组，范围从0到2π。最后，调用plot_sin_cos函数来绘制正弦和余弦曲线。

使用 pyplot 快捷函数的方法：

# # 下面是使用 pyplot 快捷函数的方法：
# 导入必要的库
import numpy as np                  # 导入NumPy库并将其命名为np，用于生成数值数据
import matplotlib.pyplot as plt     # 导入Matplotlib的pyplot模块并将其命名为plt，用于绘图# 生成 x 值
x = np.linspace(0, 2 * np.pi, 100)  # 生成一个包含100个元素的数组，从0到2π之间均匀分布的值作为x轴的数据点# 绘制正弦曲线和余弦曲线
plt.plot(x, np.sin(x), label='Sin Curve')  # 绘制正弦曲线，x为横轴数据，np.sin(x)为纵轴数据，label参数为曲线的标签
plt.plot(x, np.cos(x), label='Cos Curve')  # 绘制余弦曲线，x为横轴数据，np.cos(x)为纵轴数据，label参数为曲线的标签# 设置横纵坐标标签和标题
plt.xlabel('x')     # 设置x轴标签
plt.ylabel('y')     # 设置y轴标签
plt.title('Sine and Cosine Curves')  # 设置图形标题# 显示图例
plt.legend()        # 显示曲线的图例# 显示图形
plt.show()          # 显示绘制好的图形

这段代码使用了Matplotlib库的pyplot模块来绘制正弦曲线和余弦曲线，并对图形进行了标注和装饰。让我们逐行分析：

导入必要的库：
- numpy库用于生成数值数据。
- matplotlib.pyplot模块用于绘制图形。
生成 x 值：
- 使用numpy.linspace()函数生成一个包含100个元素的数组，表示从0到2π之间均匀分布的值，作为x轴的数据点。
绘制正弦曲线和余弦曲线：
- 使用plt.plot()函数绘制正弦曲线，参数x为横轴数据，np.sin(x)为纵轴数据，label='Sin Curve'设置曲线的标签。
- 使用plt.plot()函数绘制余弦曲线，参数x为横轴数据，np.cos(x)为纵轴数据，label='Cos Curve'设置曲线的标签。
设置横纵坐标标签和标题：
- 使用plt.xlabel()函数设置x轴标签为’x’。
- 使用plt.ylabel()函数设置y轴标签为’y’。
- 使用plt.title()函数设置图形标题为’Sine and Cosine Curves’。
显示图例：
- 使用plt.legend()函数显示曲线的图例。
显示图形：
- 使用plt.show()函数显示绘制好的图形。