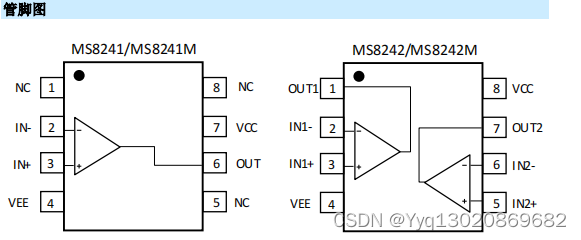
目录
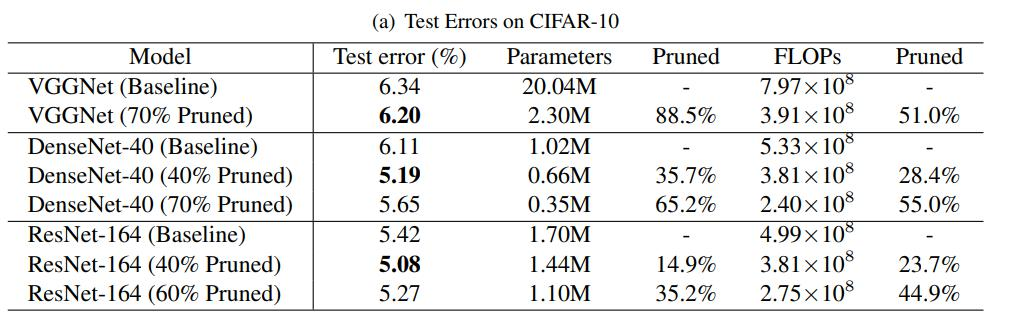
1.二分查找的时间复杂度
2.斐波那契数列及其优化
3.空间复杂度
1.二分查找的时间复杂度
我们熟知的二分查找绝对是一种很厉害的算法,因为这个算法每进行一次都会砍掉一半的数据,相当于是指数级增长,假设我们刚开始的时候数据的个数是N,我们计算时间复杂度的时候,要考虑到最坏的情况,所以应该是N/2/2/2/2……=1,最后的计算的次数就是log以2为底N的对数,在数据结构里面,为了方便起见,我们会把这里的底数省略掉,写作logN,我们见到这样结构的时候就应该明白这里实际上是省略了底数2的,但是对于其他的底数,我们一般不能省略(实际上一般也不会遇到其他的底数);
但是我们上面提到的都是二分查找的优点,其实二分查找并不常用,这个是什么原因呢?因为二分查找要求我们的数据是按照一定的顺序排列的,而且这个算法针对的是数组结构的数据,数组结构的数据无法进行数据的增删(如果想要进行数据的增删,就要让其他的数据全部前移或者后移)这样其实是很麻烦的,有些同学可能会提到链表,其实链表是无法随机的获取数据的,这个问题链表也是无能为力的,随着我们对于数据结构的学习的不断的深入,我们将会使用二叉搜索树,红黑树等结构来解决这样的问题;
二分查找的实现:分为左闭右闭区间和左闭右开区间两种情况
(1)左闭右闭区间:这个算法我们比较熟悉,实现起来也是比较容易的;
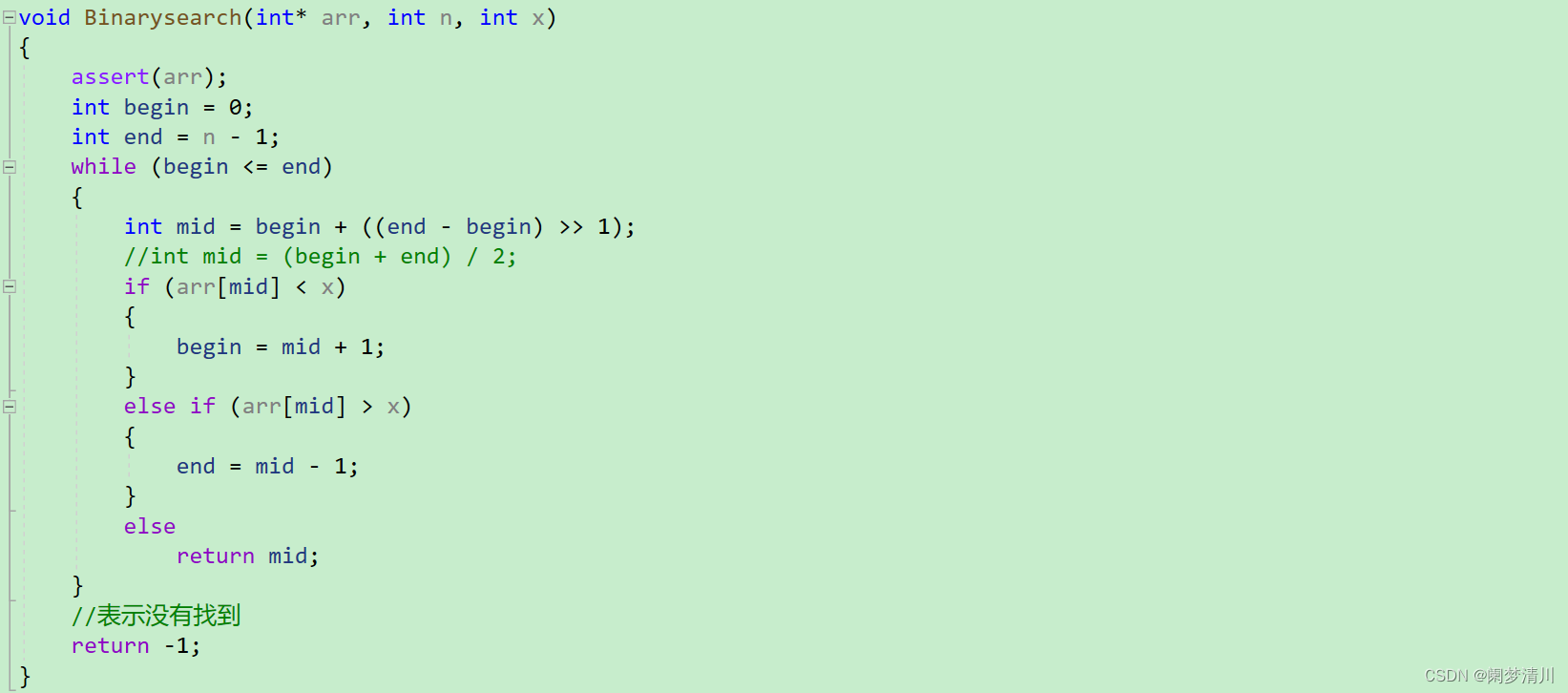
我们的mid就是取到中间值,我们的begin+end可能会越界,所以我们使用位运算符就可以解决这个问题,当然我们也是可以使用左边加右边的和除以2得到这个中间值;
(2)左闭右开区间:这个就要注意右边的开区间的取值问题;

2.斐波那契数列及其优化
下面的就是一个普通的斐波那契数列的算法,这个递归算法的时间复杂度表示的是递归的调用的次数,这个斐波那契数列的调用次数实际上是一个等比数列的求和的过程,最后求得的时间复杂度是O(2^N),当我们传递过去的N是50的时候,这个编译器计算的就很费劲了,我们可以使用循环对这个算法进行改造;

下面的循环就是改造之后的算法,我们这个时候的时间复杂度就是O(N),可见这个时候的效率是提高了很多的,这个时候我们再去计算50,就可以发现很快就得到结果;
但是实际上,这个循环的方法也是不行的,因为无论是long long类型,还是unsigned long long类型,都是有一定的数据范围的,都会造成越界的风险,在后续的C++里面,我们会使用大数算法解决这个越界的问题(简单地说大数算法就是把我们的很大的数据转换为字符串进行运算);

3.空间复杂度
空间复杂度是算法计算需要额外开辟的空间,算法本身的某些空间是不包括在内的,例如我们对于一个数组排序的算法,我们的这个数组是需要我们进行排序的,这个数组的空间并不是我们自己开辟的空间,而是题目需要我们解决问题需要的空间,这个时候数组占用的空间不属于空间复杂度的计算范围;
因为现在的计算机的空间都比较大,所以我们一般不去考虑空间复杂度,但是某些情况还是会用到的,我们那道经典的轮转数组的题目,我们之前介绍了三段逆置的方法,我们其实还可以使用创建一个新的数组,把后面的几个数据拷贝到前面,把前面的数据拷贝到后面,再把这个新的数组拷贝给原来的数组,这个过程需要额外的开辟空间,这就是以空间换时间的做法,可以提高运行效率。