目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2024年,M Han等人受到海象群体自然行为启发,提出了海象优化算法(Walrus Optimizer, WO)。


2.算法原理
2.1算法思想
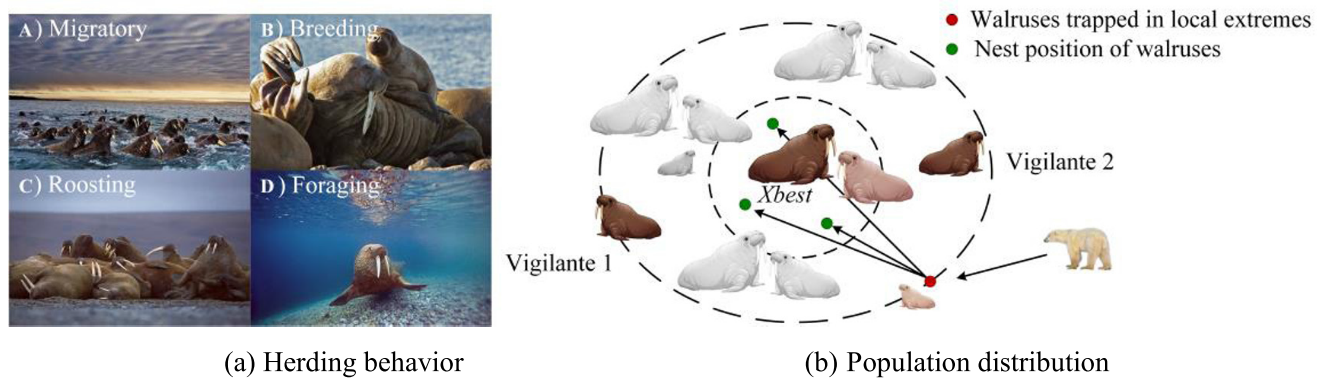
WO灵感来自海象通过接收关键信号(危险信号和安全信号)选择迁徙、繁殖、栖息、觅食、聚集和逃跑等行为。
2.2算法过程
危险信号和安全信号
海象在觅食和栖息时都非常警惕。周围会有1 ~ 2只海象作为警卫巡逻,一旦发现意外情况会立即发出危险信号。WO中的危险信号和安全信号定义:
D a n g e r _ s i g n a l = A ∗ R α = 1 − t / T A = 2 × α R = 2 × r 1 − 1 (1) Danger\_signal= A^{\ast }R\\ \alpha=1-t/T\\ A=2\times\alpha\\ R=2\times r_1-1\tag{1} Danger_signal=A∗Rα=1−t/TA=2×αR=2×r1−1(1)
A、R为危险因素,α随迭代次数t先从1减小到0,t为最大迭代次数。WO中危险信号对应的安全信号定义:
S a f e t y _ s i g n a l = r 2 (2) Safety\_signal=r_2\tag{2} Safety_signal=r2(2)
迁移行为
当危险因素过高时,海象群就会迁移到其他地区:
X i , j t + 1 = X i , j t + Migration − s t e p M i g r a t i o n _ s t e p = ( X m t − X n t ) ∙ β ∙ r 3 2 β = 1 − 1 1 + exp ( − t − T 2 T × 10 ) (3) X_{i,j}^{t+1}=X_{i,j}^t+\text{Migration}_-step\\ \mathrm{Migration\_step}=(X_m^t-X_n^t)\bullet\beta\bullet{r_3}^2\\ \beta=1-\frac{1}{1+\exp(-\frac{t-\frac{T}{2}}{T}\times10)} \tag{3} Xi,jt+1=Xi,jt+Migration−stepMigration_step=(Xmt−Xnt)∙β∙r32β=1−1+exp(−Tt−2T×10)1(3)
β是迁移步骤控制因素。
繁殖行为
在研究海象群的繁殖行为时,主要考虑了海象在陆地栖息和水下觅食这两种行为模式。海象群体分为雄性、雌性和幼年个体,每个群体成员在栖息地的选择和更新行为中表现出不同的策略,以适应环境和提高繁殖效率。
雄性海象的位置更新采用拟蒙特卡罗方法中的Halton序列,这种方法通过生成随机但均匀分布的序列来确保种群在搜索空间中的广泛分布。Halton序列的使用能够有效地均匀覆盖整个搜索区域,提高种群多样性,从而有利于在迭代过程中找到更优的解。
雌海象的位置更新则受到雄海象和领头海象的双重影响。随着迭代过程的进行,雌性海象逐渐减少对配偶的依赖,而增加对领头海象的跟随,这种策略有助于雌性海象在繁殖期间更有效地寻找食物和安全的栖息地,确保幼崽的成活率:
F e m a l e i , j t + 1 = F e m a l e i , j t + α ∙ ( M a l e i , j t − F e m a l e i , j t ) + ( 1 − α ) ∙ ( X b e s t t − F e m a l e i , j t ) (4) \begin{aligned} Female_{i,j}^{t+1} =Female_{i,j}^{t}+\alpha\bullet\left(Male_{i,j}^{t}-Female_{i,j}^{t}\right)+(1-\alpha)\bullet\left(X_{best}^t-Female_{i,j}^t\right) \end{aligned}\tag{4} Femalei,jt+1=Femalei,jt+α∙(Malei,jt−Femalei,jt)+(1−α)∙(Xbestt−Femalei,jt)(4)
海象幼崽的位置更新处于种群边缘的海象幼崽经常成为虎鲸和北极熊的目标,幼海象需要调整当前的位置以避免被捕食:
J u v e n i l e i , j t + 1 = ( O − J u v e n i l e i , j t ) ∙ P O = X b e s t t + J u v e n i l e i , j t ∙ L F (5) \begin{aligned}&Juvenile_{i,j}^{t+1}=\left(O-Juvenile_{i,j}^t\right)\bullet P\\&O=X_{best}^t+Juvenile_{i,j}^t\bullet LF\end{aligned}\tag{5} Juvenilei,jt+1=(O−Juvenilei,jt)∙PO=Xbestt+Juvenilei,jt∙LF(5)
LF为莱维飞行,水下觅食行为包括逃离和聚集行为,逃跑行为海象在水下觅食时也会受到自然捕食者的攻击,它们会根据同伴发出的危险信号逃离当前活动区域:
X i , j t + 1 = X i , j t ⋅ R − ∣ X b e s t t − X i , j t ∣ ⋅ r 4 2 (6) X_{i,j}^{t+1}=X_{i,j}^{t}\cdot R-\left|X_{best}^{t}-X_{i,j}^{t}\right|\cdot{r_{4}}^{2}\tag{6} Xi,jt+1=Xi,jt⋅R− Xbestt−Xi,jt ⋅r42(6)
海象可以根据种群中其他海象的位置合作觅食和移动,共享位置信息可以帮助整个海象群找到食物丰富度更高的海域:
X i , j t + 1 = ( X 1 + X 2 ) / 2 { X 1 = X b e s t t − a 1 × b 1 × ∣ X b e s t t − X i , j t ∣ X 2 = X s e c o n d t − a 2 × b 2 × ∣ X s e c o n d t − X i , j t ∣ a = β × r 5 − β b = tan ( θ ) (7) \begin{aligned} &X_{i,j}^{t+1}=(X_{1}+X_{2})/2 \\ &\left.\left\{\begin{array}{c}X_1=X_{best}^t-a_1\times b_1\times\left|X_{best}^t-X_{i,j}^t\right|\\\\X_2=X_{second}^t-a_2\times b_2\times\left|X_{second}^t-X_{i,j}^t\right|\end{array}\right.\right. \\ &a=\beta\times r_{5}-\beta \\ &b=\tan(\theta) \end{aligned}\tag{7} Xi,jt+1=(X1+X2)/2⎩ ⎨ ⎧X1=Xbestt−a1×b1× Xbestt−Xi,jt X2=Xsecondt−a2×b2× Xsecondt−Xi,jt a=β×r5−βb=tan(θ)(7)
伪代码

3.结果展示
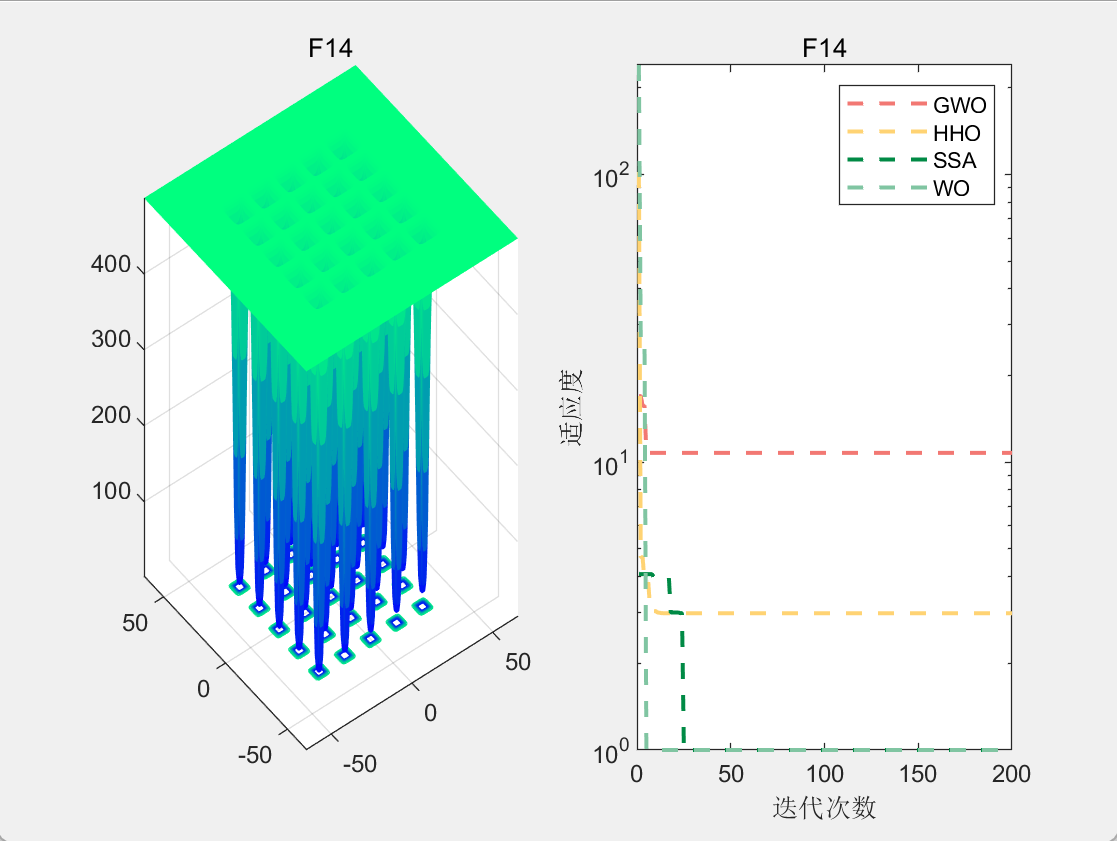
使用测试框架,测试WO性能 一键run.m
- 【智能算法】省时方便,智能算法统计指标——一键运行~
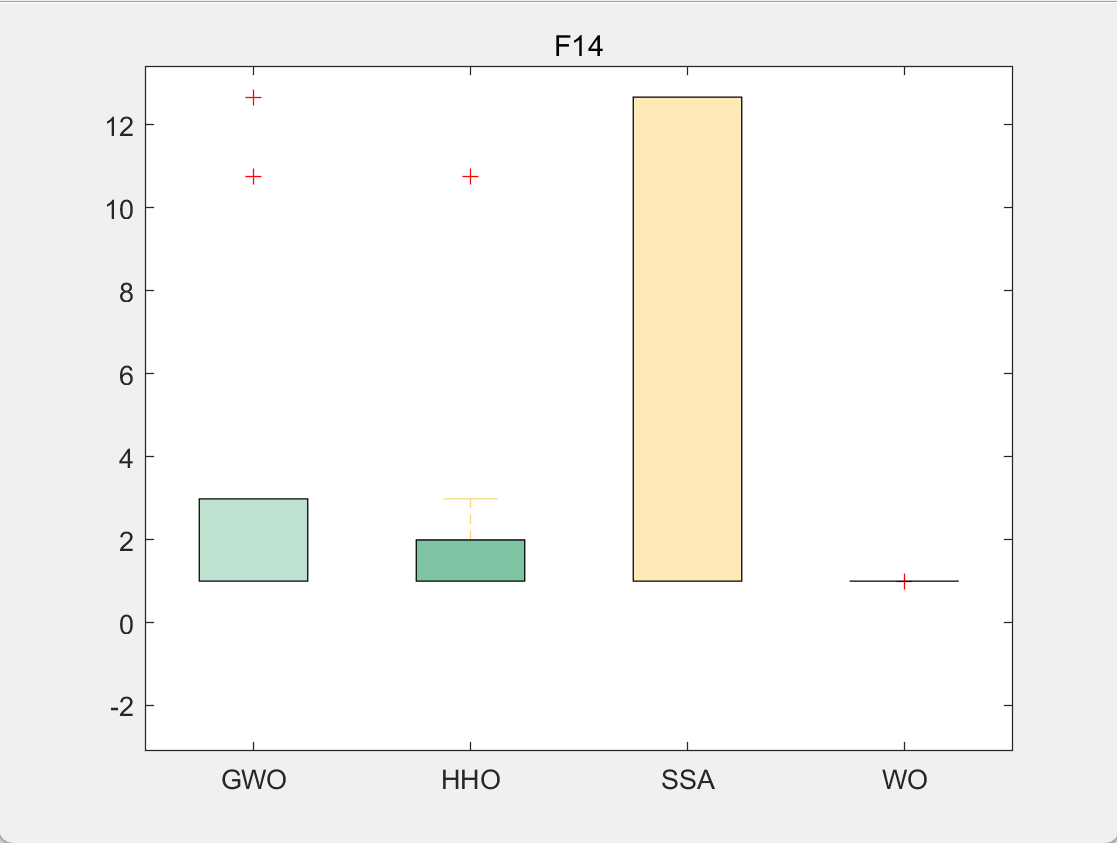
CEC2005-F14
4.参考文献
[1] Han M, Du Z, Yuen K F, et al. Walrus optimizer: A novel nature-inspired metaheuristic algorithm[J]. Expert Systems with Applications, 2024, 239: 122413.