论文概述
推荐系统的矩阵分解技术可以为用户提供更为准确的个性化推荐,对比传统的近邻技术,矩阵分解技术可以纳入更多信息,如隐式反馈、时间效应和置信度
近邻技术:基于用户或物品之间的相似性进行推荐,当用户之间已有评价计算出两个用户爱好类似,就将a用户的其他物品推荐给b
矩阵分解技术:把原来的大矩阵,近似分解成两个小矩阵的乘积,在实际推荐计算时不再使用大矩阵,而是使用分解得到的两个小矩阵。
论文内容
推荐系统策略
1. 为每一个用户或者项目创建一个档案记录特征,通过这些资料,系统可以将用户和匹配的产品联系起来
2. 协同过滤:依赖于用户过去的行为,分析用户之间的关系和产品之间的关系,按照群体行为去推荐,寻找和a相似的用户群体,将这些群体的爱好推荐给a
邻域方法:一个用户评价了产品A是好,那么他很有可能给A的相似产品B也评价好;当两个用户有很相似的爱好,那么他们之间的评分也可以互相补充
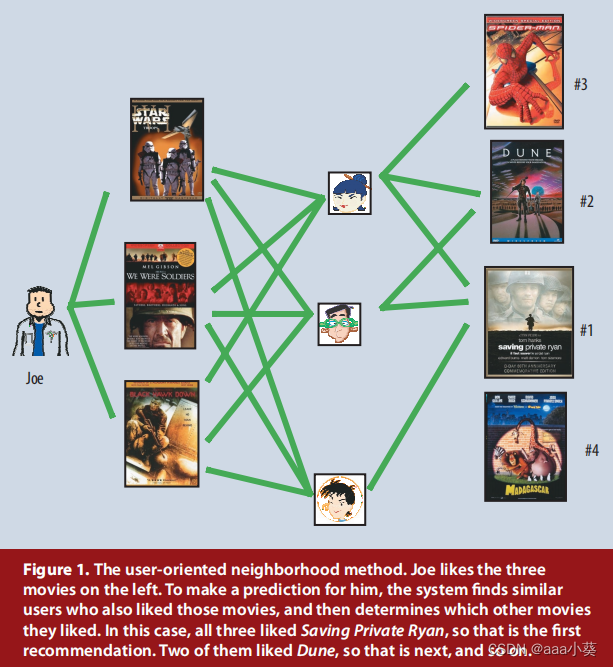
潜在因素模型:通过分析大量的用户评分,可以大概知道影响评分的一些潜在因素,比如你给戏剧电影很高评价,那么系统会认为戏剧这个特征就是一个潜在因素,当有新的戏剧出现就会给你推荐,利用一个二维模型简化说明,我们可以预测Gus可能对Dumb and Dumber的评分较高,而对Braveheart评分一般,不喜欢The Color Purple

横坐标表示用户的性别导向,纵坐标表示电影积极或消极,将用户和项目(电影)按照已有评价分析后放入图中,每个项目i对应一个向量qi,每个用户u对应一个pu,两者的点积越大,说明该用户对此项目偏爱程度更高
当一些用户可能并没有对某些电影做出评价,我们也可以通过该方法估算用户u对项目i的评分r
基本矩阵因式分解模型
将上述二维坐标扩展,将用户和项目映射到维数f的联合潜在因子空间,用户和项目的交互可以建模为空间的内积,捕获了用户和项目之间的交互,公式1表示预测的用户和项目之间的交互
该模型的主要挑战就是系统需要找到每个项目和用户映射的向量qi和pu,这个模型和SVD技术密切相关
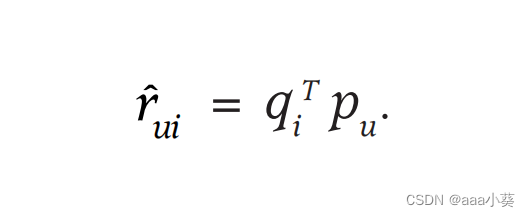
奇异值分解SVD技术:
将一个大矩阵分解为三个部分,第一个部分告诉我们数据的主要方向,第二个部分告诉我们每个方向的重要性有多大,第三个部分则是另一个角度的数据主要方向。,但是当数据稀疏性很高,会导致过拟合状态
损失函数
早期为了解决稀疏性问题采用填补空缺值,但是往往不准确的估计值会扭曲数据,我们只对已有的评分建模,该系统通过拟合先前观察到的评级来学习模型。

公式2为SVD的损失函数,系统会最小化已知评分集合上的正则化平方误差,在加号左边是最小化预测评分与实际评分之间的差异,加号右侧是正则化项(也叫惩罚项)用于控制模型的复杂度;可以防止出现过拟合状态
优化算法
最小化该上述方程有两个方法:随机梯度下降法和交替最小二乘法
随机梯度下降法
随机梯度下降(SGD)就像是在一座大山的地图上寻找最低点,但你不能看到整个地形,只能通过不断随机挑选一些地方来感受坡度,然后沿着坡度最大的方向小步向下走,希望最终能找到那个最低点。
随机梯度下降是一种迭代的优化算法,它在每次迭代中只使用一个或一小批训练样本来更新模型参数。这种方法的优点是在大规模数据集上效率较高,因为不需要在每次迭代时处理整个训练集。
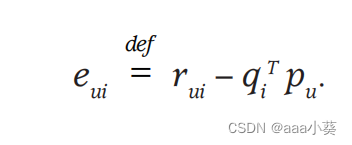
公式3表示给出训练集(u,i),系统会给出预测值qiTpu,然后用真是的计算值r减去预测值,得到误差预测值
接着我们要优化更新参数q和p,见公式4

首先,我们有一个误差项 e,它表示模型对第 𝑖i 个样本的预测和实际值之间的差距。然后,我们有一个学习率 γ,它决定了我们根据这个误差调整模型参数的幅度,就像你决定每次走多远一样。接下来,我们用这个误差和学习率来更新参数qi 和 pu。更新的过程就是让参数朝着减少误差的方向迈出一步,这一步的大小由学习率 γ 和误差 e 共同决定。
但是对于数据少或者需要更精确的状态还有一种方法:交替最小二乘法
交替最小二乘法ALS
每次固定一个因子向量(比如qi),改变另一个因子向量(pi),如此反复交替直到收敛,利用ALS系统可以并行化,即可以同时计算多个因子向量,当面对隐式项目集的时候,训练集很难采用梯度下降,此时就可以利用ALS技术来优化算法
增加偏差
有时候有些用户会偏向于打低分,有些用户即使物品不喜欢也偏向于高分,有时候某些项目可能推出优惠劵等于是有高分,也并不代表用户就喜欢,也有可能某个平台就是限制评分等操作,所以我们往往要考虑这些偏差
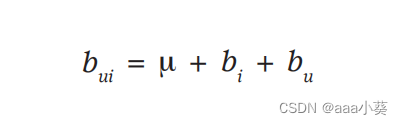
总体平均评分用µ表示;参数bu和bi分别表示用户u和第i项与平均值的观测偏差,公式5表示用户和项目的交互偏差(用户对项目的偏好估计可能会产生的误差)
现在,假设µ对所有电影的平均评分是3.7星。此外,《泰坦尼克号》比一部普通电影要好,所以它的评分往往比平均电影高出0.5颗星。另一方面,乔是一个关键的用户,他的评分往往比平均水平低0.3颗星。因此,乔对《泰坦尼克号》的评级估计为3.9颗星(3.7 + 0.5 - 0.3)。
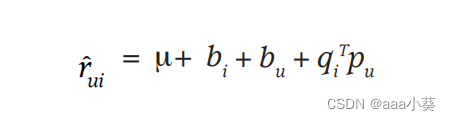
公式6在原有的用户和项目的交互算法上加入了偏差,现在右边四个值分别表示全局平均值、项目偏差、用户偏差和用户项目交互,从而使得结果更准确
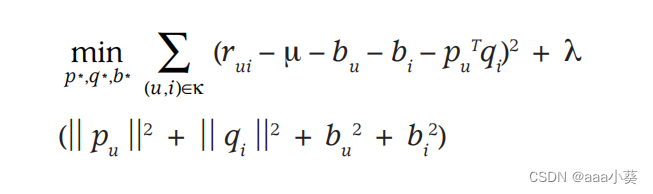
公式7在原来的损失函数上做了一些改变,添加了偏差项,对其建模非常重要
其他输入源
通常,一个系统必须处理冷启动问题,其中许多用户提供很少的评级,使它很难对他们的品味得出一般性的结论。缓解这个问题的一种方法是合并关于用户的其他信息来源。推荐系统可以使用隐式反馈来深入了解用户的偏好。

- N(u)表示用户u的隐式偏好项目集
- A(u)表示用户u对应的属性集(性别、年龄、家庭等)
- xi表示用户的隐式爱好集内每个项目的对应向量,这个累加和反映了用户 u 对项目集中所有项目的因素向量的综合偏好
为了使得这个累加和更有意义,通常会进行规范化处理。规范化可以帮助我们调整不同用户之间项目集大小的差异,以及防止偏好向量的长度变得过大,导致模型不稳定。一个常见的规范化方法是减去一个比例因子,例如项目集大小的0.5倍
时间动态
在公式6的基础上,给项目偏差、用户偏差、用户偏好向量都加上了时间的概念,因为物品本身不像人,基本特征是不会变化,可以视为静态
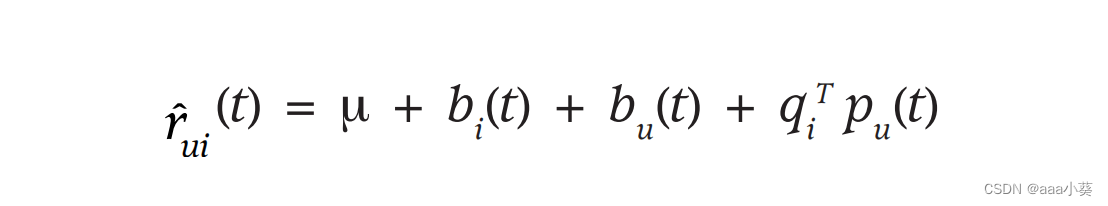
- 第一个时间效应解决了这样一个事实,即一件物品的受欢迎程度可能会随着时间的推移而改变。例如,电影可能会被外部事件引发,比如演员在新电影中的出现。因此,这些模型将项目偏差b视为时间的函数。
- 第二个时间效应允许用户随着时间的推移而改变他们的基线评级。例如,一个倾向于给平均电影“4星”的用户现在可能会给这样的电影评级“3星”。这可能反映了几个因素,包括用户评分量表的自然漂移,用户相对于其他最近的评分,以及家庭成员的身份会随着时间的推移而改变。因此,在这些模型中,参数bu是一个时间的函数。
- 第三个时间效应使得用户会随着时间的推移而改变他们的偏好。例如,一个心理惊悚片类型的粉丝可能会在一年后成为犯罪剧的粉丝。类似地,人类也是在改变了他们对某些演员和导演的看法。该模型通过将用户因素(向量pu)作为时间的函数来解释这种效应。
不同置信度的输入
矩阵分解模型可以很容易地接受不同的置信水平,这让它给不太有意义的观察更少的权重。如果对观察 r 的信心表示为 c ,那么模型将可以增强成本函数
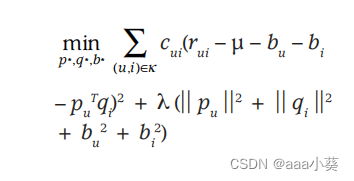






![正点原子[第二期]Linux之ARM(MX6U)裸机篇学习笔记-5](https://img-blog.csdnimg.cn/direct/4e7f027b22d8431ba6068716f791f717.png)