目录
1、引入
2、位图的概念
3、位图的实现
①框架的搭建
②设置存在
③设置不存在
④检查存在
4、位图计算出现的次数
5、完整代码
1、引入
我们可以看一道面试题
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在 这40亿个数中。【腾讯】
常用可能有三种解决方式:
🟢遍历,时间复杂度O(N)
🟢排序(O(NlogN)),利用二分查找: logN
遍历和排序查找的工程量太大了,这肯定是不行的,因为,光是把数据存起来就要用掉16GB的内存,而且要求空间连续内存开不出这么大的连续空间。所以最佳是用位图来解决。
🟢位图解决 数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一 个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0 代表不存在。

2、位图的概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
我们都知道计算机的数据和指令都是二进制的,二进制是由0,1两个数字组成,这就意味着这两个数字可以表示两个不同的状态,位图的基础也是基于这一点。
所以,我们利用这一点。假设我们现在有一堆海量的数据,我可以通过某种方式让数字对应到相应的二进制的数位上,同时规定0表示该数字不存在,1表示存在。这本质上也是一种哈希的思想。
3、位图的实现
我们想要的位图大概是这一种:所以我们需要两个变量,一个计算数据在哪一个32位里,一个计算是32中的哪一位。

①框架的搭建

②设置存在
我们需要找到相应的位置,如果存在就变成1,如果不存在就不变。
比如有一个数字150,我们要将他插入到位图中,并将相对应的位图变为1.

现在我们找到了相应的位置,现在我们要将这个位从0变成1,表示241已经存在,但是我们不能影响其他位的状态,这个时候我们可以使用位运算:
步骤:
我们使用1,1的二进制是0000 0000 0000 0000 0000 0000 0000 0001
将1的二进制向左移动 j 个位置
原二进制和这个位置采取或运算,有1为1,如果都为0为0;


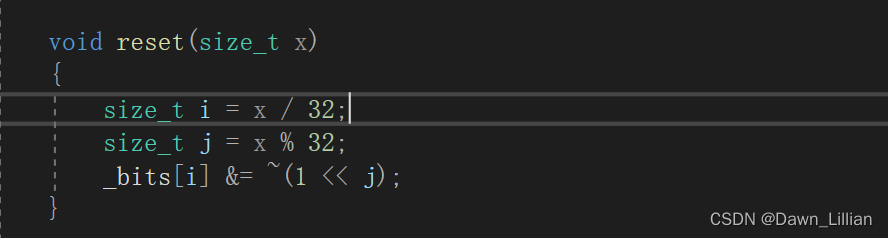
③设置不存在
找到了相应的位置,将这个位从1变成0,这个时候我们可以使用取反+&运算:
步骤
我们使用1,1的二进制是0000 0000 0000 0000 0000 0000 0000 0001
将1的二进制向左移动 j 个位置
按位取反
原二进制和这个位置采取按位与运算,有0为0,都为1为1;

④检查存在
步骤:
我们使用1,1的二进制是0000 0000 0000 0000 0000 0000 0000 0001
将1的二进制向左移动 j 个位置
原二进制和这个位置采取按位与运算,有0为0,都为1为1;
一个整型值只要有一位为1就是非0,非0就是真。

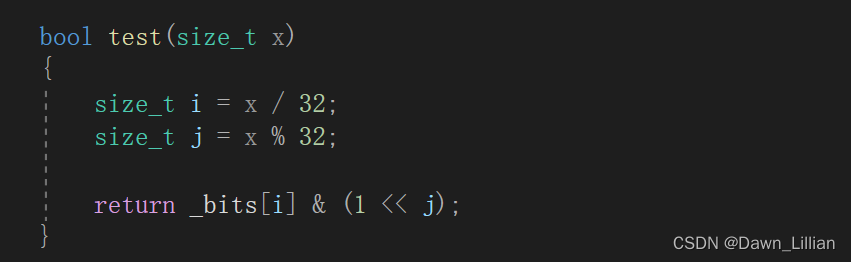
【代码检查】
 4、位图计算出现的次数
4、位图计算出现的次数
上述我们封装好了一个位图,但是我们只是解决了数据的储存,我们还没有解决如何只找出出现一次的数。我们可以将数字分为三种状态:
一次都没有出现的,出现一次,出现两次及以上。
因此可以再次封装一个位图来寻找只出现了一次的数,两个位图合起来表示数据出现的次数:
00 表示一次都没有出现过
01 表示出现一次
10 表示出现两次及以上
用两个位图来实现:

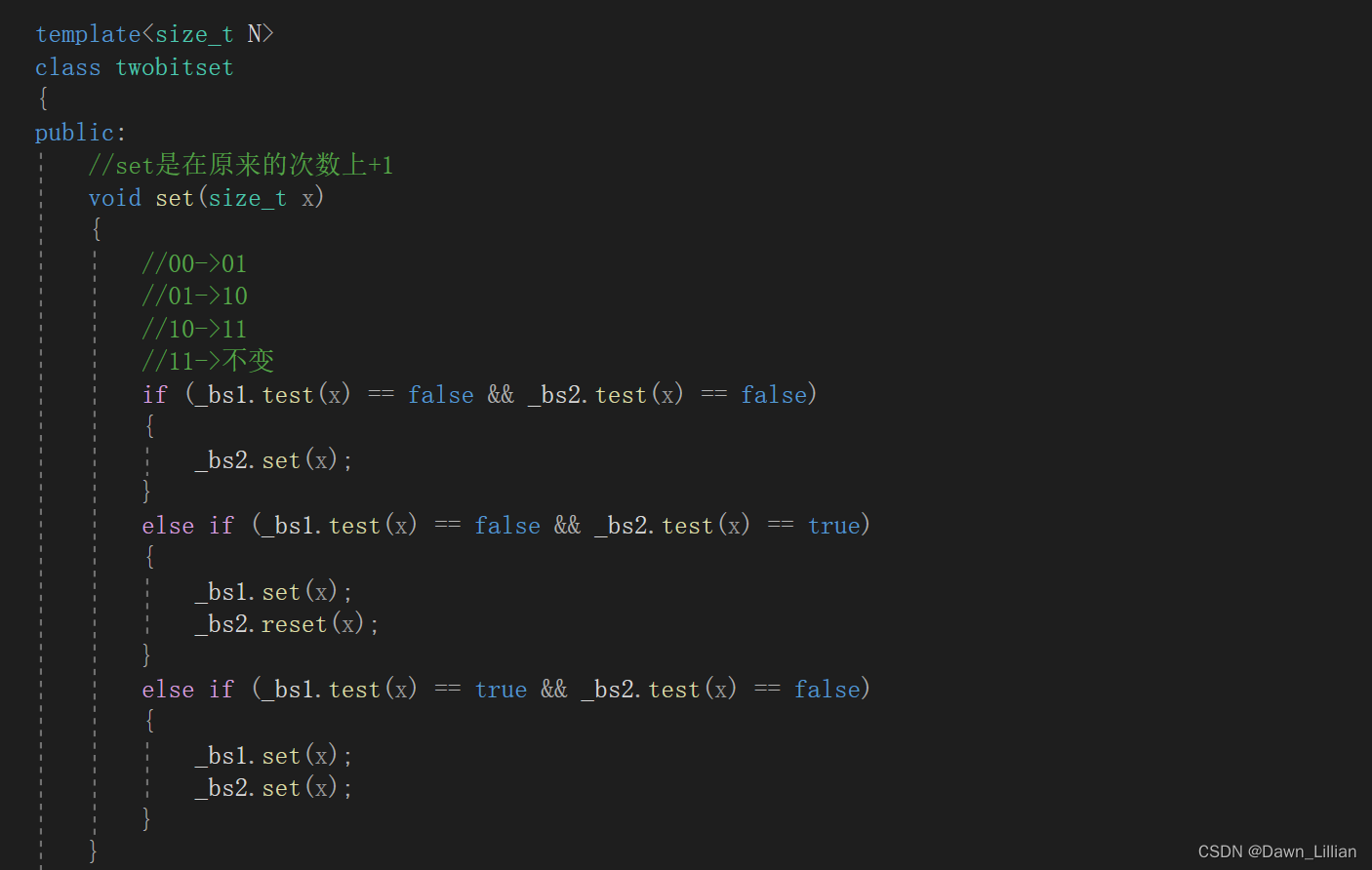
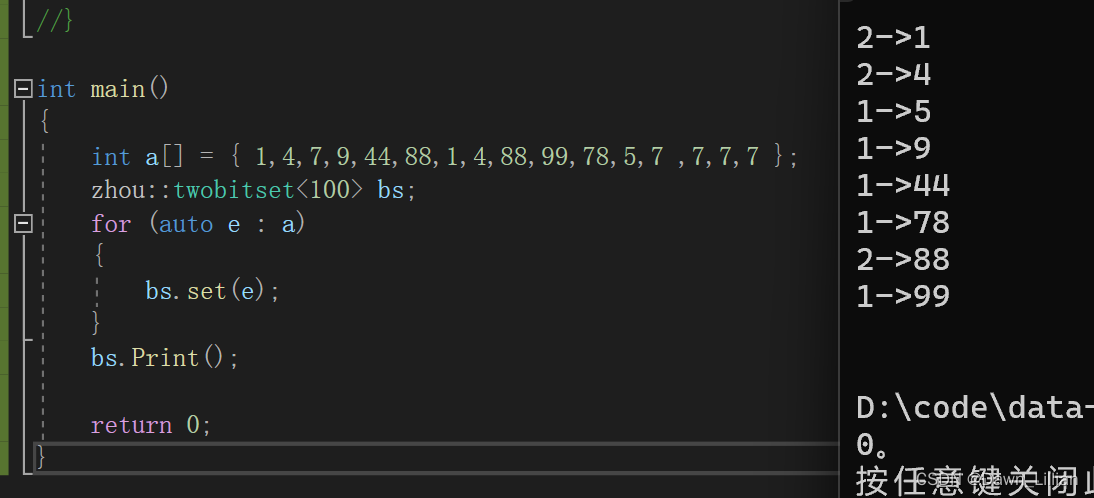
可以定义一个打印函数,将其打印出来

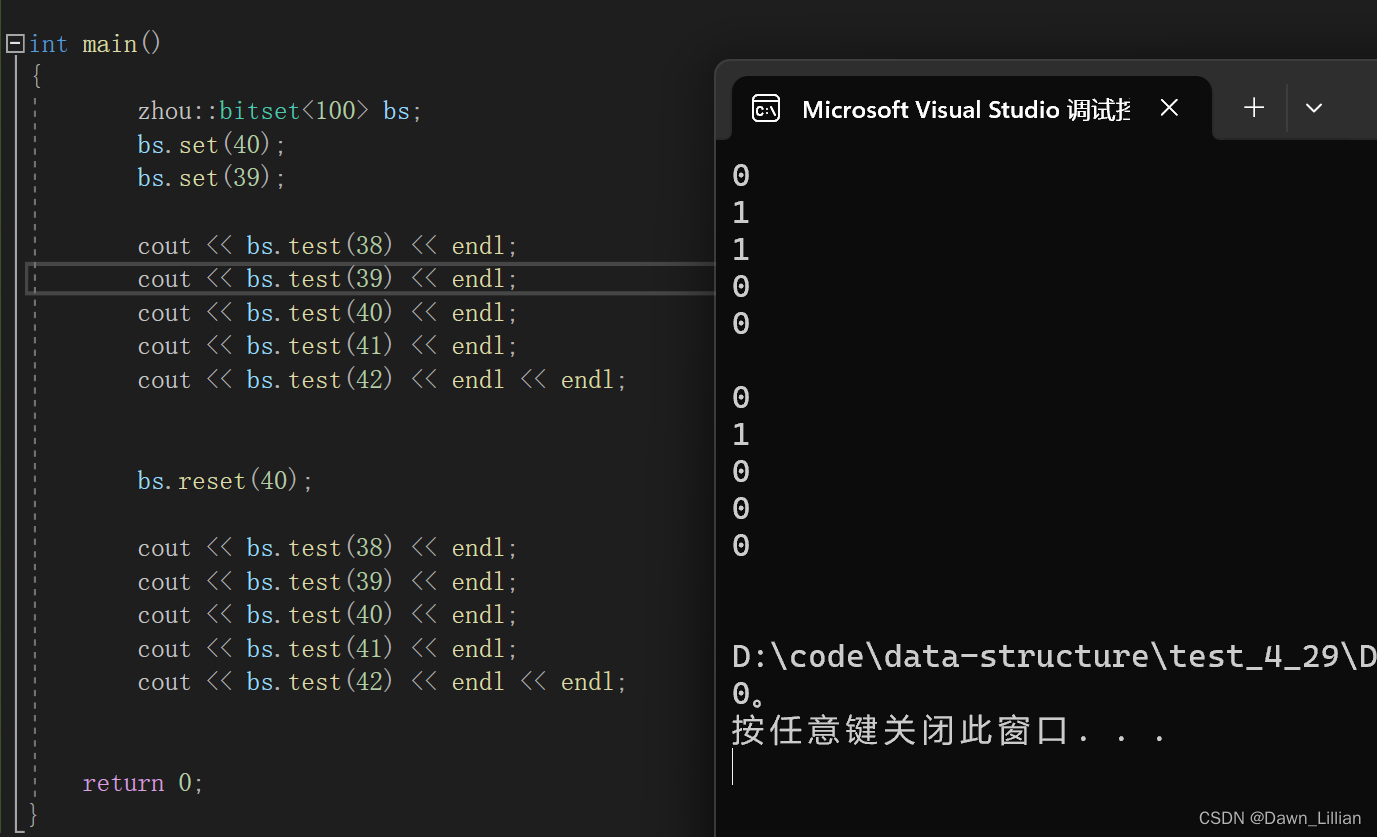
【代码检查】
【总结】
位图的优点
速度快,节省空间
缺点:只能映射整型
5、完整代码
#define _CRT_SECURE_NO_WARNINGS
#pragma once
namespace zhou
{// N是需要多少比特位template<size_t N>class bitset{public://计算出需要多少空间,如果不是32的倍数,多开辟一个字节bitset(){_bits.resize(N/32+1, 0);}//将对应的 j 设置为1void set(size_t x){size_t i = x / 32;size_t j = x % 32;_bits[i] |= (1 << j);}void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);}private:vector<int> _bits;};template<size_t N>class twobitset{public://set是在原来的次数上+1void set(size_t x){//00->01//01->10//10->11//11->不变if (_bs1.test(x) == false && _bs2.test(x) == false){_bs2.set(x);}else if (_bs1.test(x) == false && _bs2.test(x) == true){_bs1.set(x);_bs2.reset(x);}else if (_bs1.test(x) == true && _bs2.test(x) == false){_bs1.set(x);_bs2.set(x);}}void Print(){for (size_t i = 0; i < N; i++){if (_bs1.test(i) == false && _bs2.test(i) == true){cout << "1->" << i << endl;}else if (_bs1.test(i) == true && _bs2.test(i) == false){cout << "2->" << i << endl;}}cout << endl;}private:bitset<N> _bs1;bitset<N> _bs2;};
}