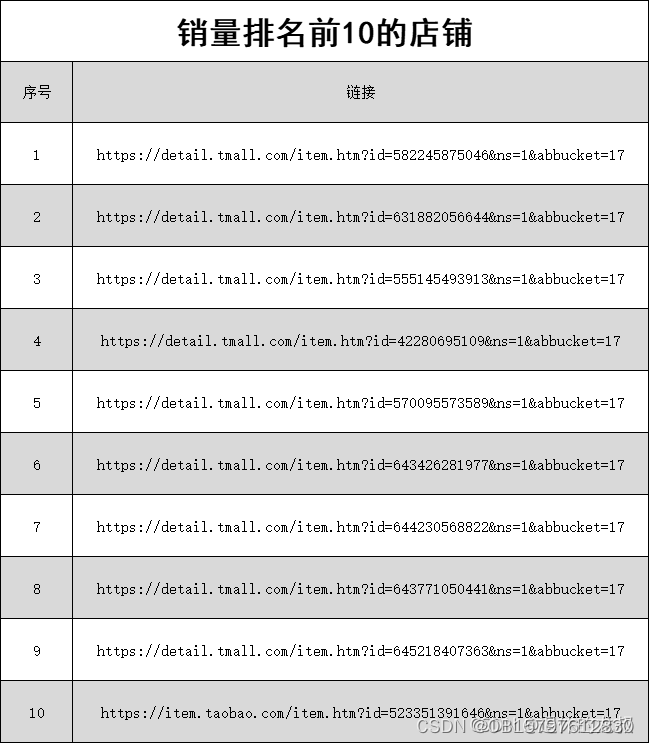
1.第1章  MATLAB系统环境

1.1

注：plot函数为画图函数。例plot（x1,y1,':',x2,y2,'*'）;

1.2

注：root为求根函数。p为方程变量前面系数矩阵。

1.3

注：

2*x+3y-1*z = 2;

8*x+2*y+3*z = 4;

45*x+3*y+9*z = 23

求：x,y,z的值

注：inv为求逆函数。

1.4

注：@（x）是匿名函数，这个x是可以被使用的，理解如下：

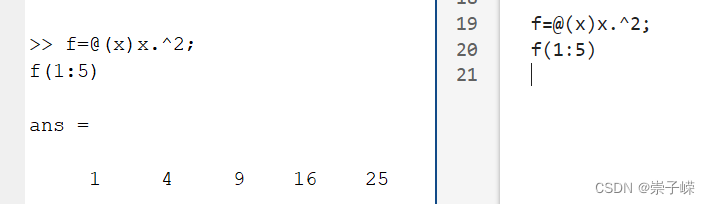
2.第2章  MATLAB数据及其运算

2.1

2.2

注：rem（A，3）的结果如果为0，返回1，负责返回0。

2.3

注：字符串可以像数组一样被应用。由于ch（k）=ch(k)-('a'-'A')结果为对应的ascci码值，所以后面要使用char函数，变回字符串。如下

3. 第3章  MATLAB矩阵分析与处理

3.1

注：magic（a），生成大大小为a*a的矩阵，并且行和列之和一样。

3.2

注：

D*A，由线性代数知识可知，D的第一行乘以A的第一列放在第一个，依此类推。

3.3

注：（1）b=[5，-2，6]‘，是行向量的转置变成列向量。

        （2）inv函数为取逆函数。

补充：

（1）det函数为求矩阵行列式。

（2）rank函数为求矩阵的秩。

（3）trace函数为求矩阵的迹。

（4）norm函数为求矩阵范数。

（4）eig函数求矩阵的特征向量和特征值。

4.第4章  MATLAB程序流程控制

4.1

法一：使用脚本

法二：使用函数（调用函数时，用使用函数文件名）

4.2

注：使用input函数输入a，b，c的值，使用求根公式（-b+sqrt(b^2-4*a*C)）/(2*a)求出根。

4.3

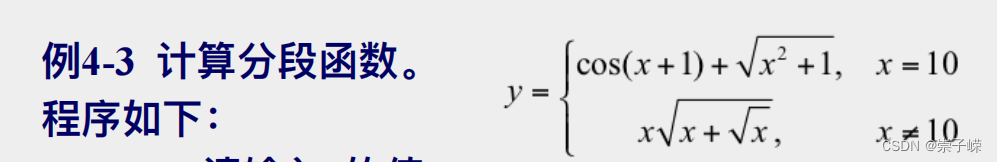
4.4

注：可以将所有的setstr换成char，一样的效果。

4.5

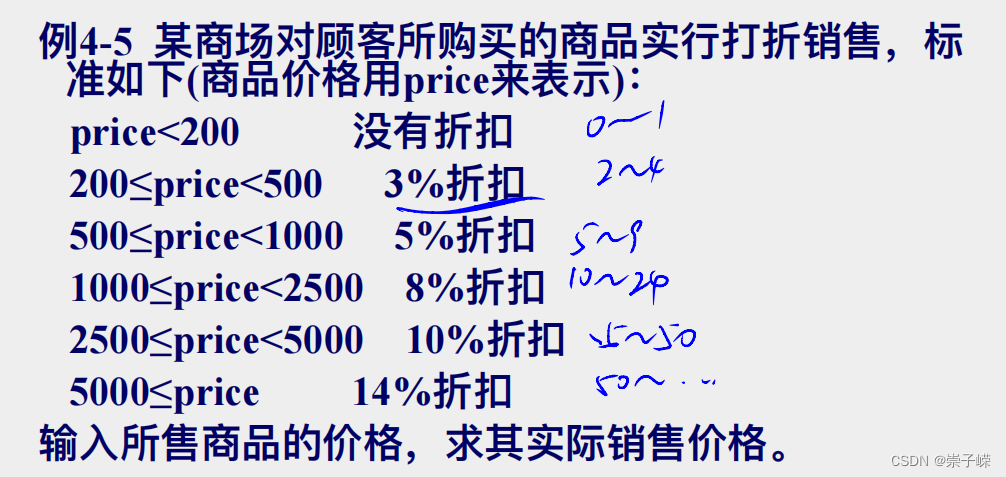
注：在switch case语句中，如果case的值同时为多个时，使用元胞数组{}。

4.6

注：fix为取整函数，rem为取余函数。

4.7

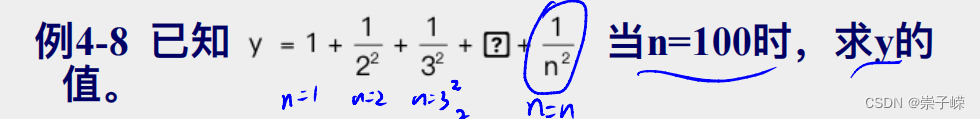
法1：

法2：

注：将1~n放在一个变量里面变成行向量，同时对这个行向量进行操作。

4.8

注：将整块面积分割成若干个小矩形。

4.9 *

注：a为4*3的矩阵，k=a，k一次取一列，所以一共取3次。

4.10

注：变量sum为所以数之和，sum/n是平均数。

4.11

注：

（1）continue为跳过一次循环中的其他语句，进行下一次循环。

（2）break为跳出整个循环。

4.12

4.13

注：nargin为函数输入时的变量个数。

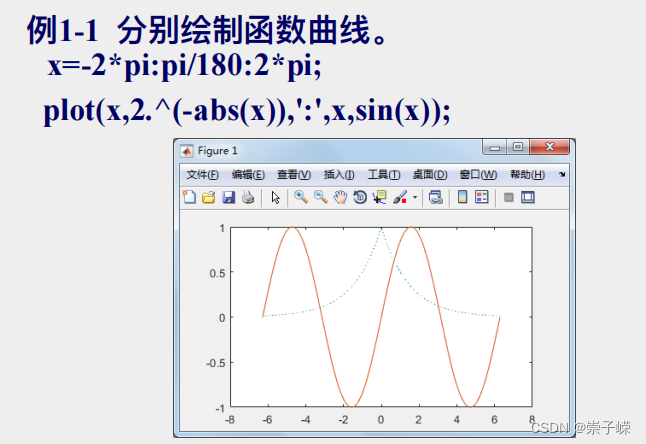
5.第5章  MATLAB绘图

5.1

注：

5.2

5.3

5.4

5.5

5.6

注：plotyy函数可以将不同的量纲的函数放在统一坐标下。

5.7

5.8

注：subplot函数对窗口进行分割。

补充：

（1）

（2）

（3）

（4）

注；选项为stacked或grouped

（5）

5.9

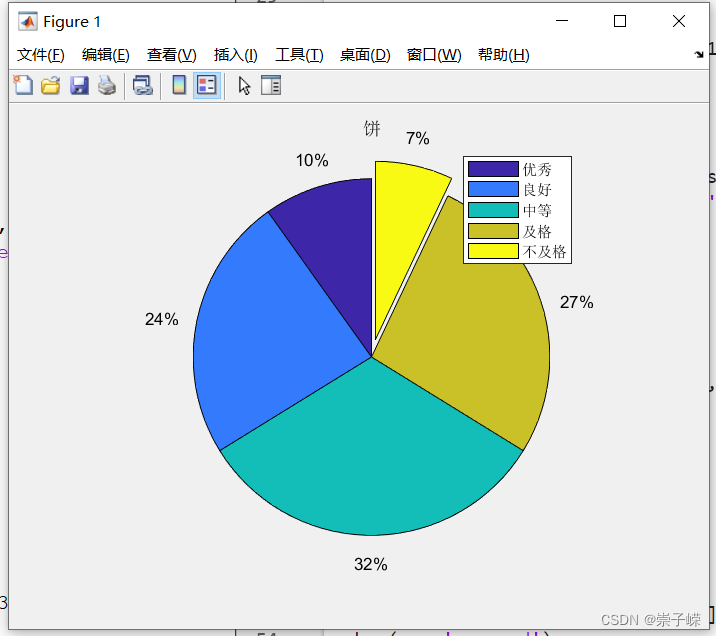
注：给1为突出，给0为不突出

5.10

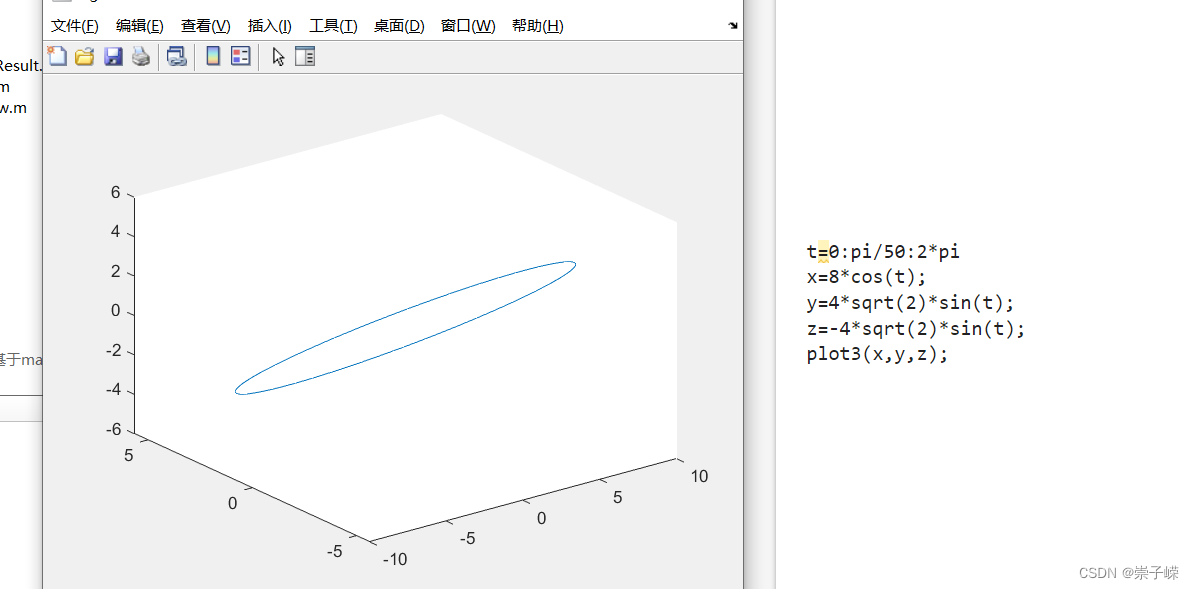
5.11

注：meshgrid画网格线

5.12

5.13

5.14

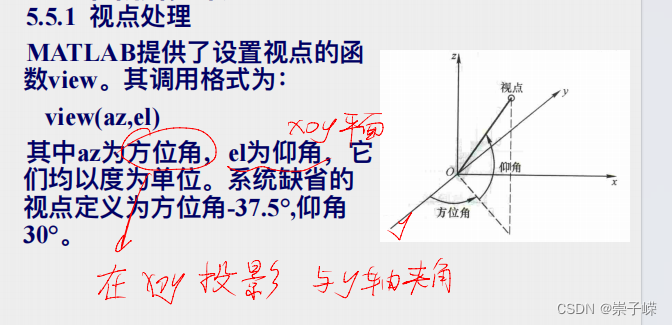
6.第6章  MATLAB数据分析与多项式计算

6.1

注：max函数为求最大值函数。max（a）求每一列的最大值，max（a，[]，2）求每一行的最大值。

6.2

6.3

注：

（1）sum为求和函数，sum（a，1）为按列求和。sum（a，2）为按行求和。

（2）prod函数为求乘函数，用法与sum一样。

（3）mean函数为求平均值函数，用法与sum一样。

（4）cumsum函数为累加和函数，用法与sum一样。

（5）cumprod函数为累积和函数，用法和sum一样。

6.4

6.5

注

6.6

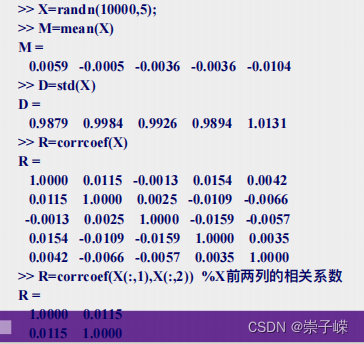
注：corrcoef函数为求相关系数函数，

6.7

注：sort为排序函数

6.8

注：多项式加法时，前一项最高次和后一项最高次不同时，较低的需要将高次补0直到与前一项最高次相同，以便于计算。

6.9

注：conv函数用于求多项式之间的乘积。

6.10

注：deconv函数用于多项式之间的除法。

6.11

注：polyder函数用于多项式的求导。

6.12

注：polyval为代数多项式函数，求指定的x时的y值

补充：polyvalm函数为求代数矩阵多项式。与polyval不同的是：

6.13

注：

（1）roots为求多项式根函数

（2）roots求出来的值，带入poly函数可以求出原函数。

6.14

对比：结果与原函数差一个系数3。

6.15

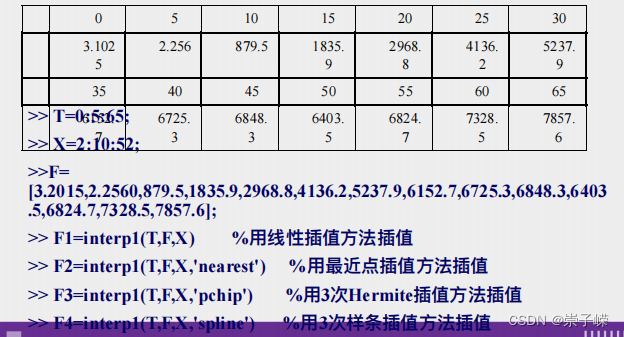
注：interp1为一维插值函数。

其中，X,Y为需要被插值函数的x和y，X1是你需要插值的点，method为你选择的插值方式：

补充：interp2为二维插值函数，其插值模式与interp2一样。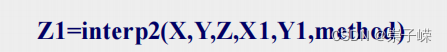

6.16

注：在指定点处插值

（1）interp2（x，y，Z，0.5，0.5），在（0.5，0.5）处插值

（2）interp2（x，y，Z，[0.5,0.6]，0.4），在（0.5，0.4）和（0.6，0.4）处插值

（3）interp2（x，y，Z，[0.5,0.6]，[0.4,0.5]），在（0.5，0.4）和（0.6，0.5）处插值

（4）interp2（x，y，Z，[0.5,0.6]’，[0.4,0.5]），在（0.5，0.4）和（0.5，0.5）和（0.6，0.5）和（0.6，0.4）处插值。

找规律，当为两个大小相同的行向量时，一个行向量的x仅仅与另一个行向量的y值对应。当一个为行向量一个为列向量时，一个行向量的x值与另一个列向量的所有y对应。

6.17*

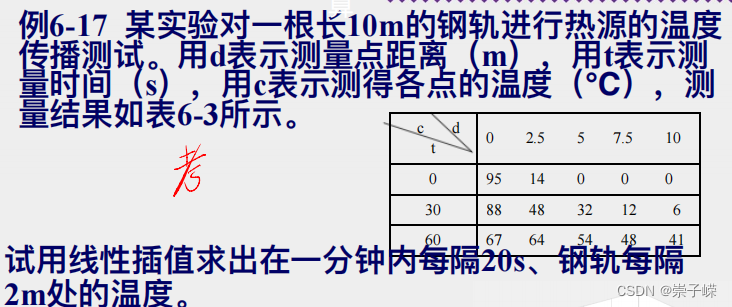
注：这个的t和ti都为列向量都是因为需要编制二维模型，只有一个为u行向量一个为列向量时才可以实现，所以要取反。

6.18

注：

（1）linspace（0，2*pi，50）等价于 0：50/pi：2*pi，用于创建数据

（2）polyfit为拟合函数，用于通过已知条件来预测给定点的值。