搜索算法系列之四(斐波那契)

以下算法被验证过，如有什么问题或有补充的欢迎留言。

前言

斐波那契数列，又称黄金分割数列，是由意大利数学家（Leonardo Fibonacci）在1202年提出的。这个数列的递推关系是F(0)=1，F(1)=1，F(n)=F(n-1)+F(n-2)(n≥2，n∈N*)，即每一项都是前两项的和。

斐波那契数列在自然界、数学、物理、工程技术和艺术等多个领域都有广泛的应用。

算法原理

斐波那契搜索算法是一种基于斐波那契数列的分割搜索技术，旨在优化查找过程的效率。它的原理可以概括如下：

斐波那契数列的选择：
- 首先，我们需要选择一个斐波那契数列，这个数列的长度应该比待搜索数组的长度略大。通常，选择的斐波那契数列是递增的，并且长度满足斐波那契数列的定义：每个数字是前两个数字之和。
计算斐波那契数列中的两个相邻数：
- 根据选定的斐波那契数列，计算相邻的两个斐波那契数列值，记为 fib1 和 fib2。
定义偏移量和搜索范围：
- 初始时，定义一个偏移量 offset 为 -1，表示初始搜索范围为整个数组。
- 定义搜索范围的上限为 fib1 或 n - 1 中较小的一个。
开始搜索：
- 在每一轮的搜索中，比较当前偏移量加上 fib2 的位置处的元素与待搜索的关键字。
- 如果当前位置处的元素小于关键字，则说明关键字可能在当前位置的右侧，因此将搜索范围限制在右侧，并更新偏移量和斐波那契数列值。
- 如果当前位置处的元素大于关键字，则说明关键字可能在当前位置的左侧，因此将搜索范围限制在左侧，并更新偏移量和斐波那契数列值。
- 如果当前位置处的元素等于关键字，则搜索成功，返回当前位置的索引。
迭代搜索：
- 继续以上步骤，直到搜索范围缩小到只包含一个元素，或者直到找到关键字为止。

斐波那契搜索算法的核心思想在于通过斐波那契数列来定义搜索范围的分割点，从而实现更高效的搜索过程。与二分搜索类似，它也是一种分治策略，但相对于二分搜索，斐波那契搜索算法在某些情况下具有更好的效率，特别是当搜索的数组长度不是 2 的幂次方时。

代码实现(c)

#include <stdio.h>// 定义斐波那契搜索算法
int fibonacciSearch(int arr[], int n, int key) {int fib2 = 0; // (m-2)th Fibonacci numberint fib1 = 1; // (m-1)th Fibonacci numberint fib = fib1 + fib2; // mth Fibonacci number// 找到斐波那契数列中最接近数组长度的数while (fib < n) {fib2 = fib1;fib1 = fib;fib = fib1 + fib2;}int offset = -1; // 偏移量while (fib > 1) {int i = (offset + fib2) < (n - 1) ? (offset + fib2) : (n - 1);if (arr[i] < key) {fib = fib1;fib1 = fib2;fib2 = fib - fib1;offset = i;} else if (arr[i] > key) {fib = fib2;fib1 = fib1 - fib2;fib2 = fib - fib1;} else {return i; // 找到了，返回索引}}// 没有找到return -1;
}int main() {int arr[] = { 10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100 };int n = sizeof(arr) / sizeof(arr[0]);int key = 45;int index = fibonacciSearch(arr, n, key);if (index != -1) {printf("找到了数字 %d ，位于索引 %d 处。\n", key, index);} else {printf("未找到数字 %d 。\n", key);}return 0;
}

示例演示

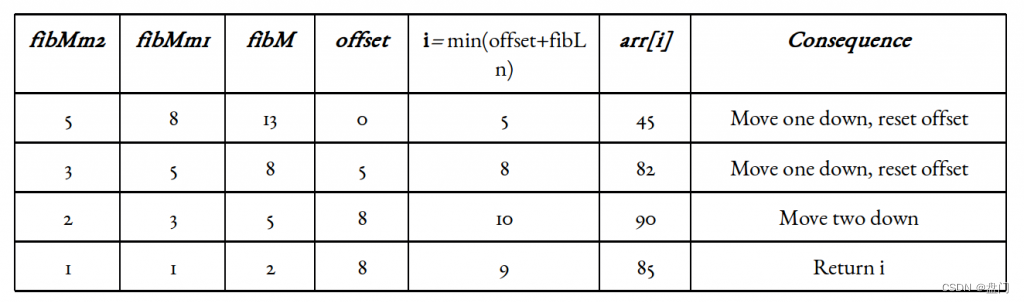
说明假设：基于1的索引。目标元素x为85。阵列的长度n=11。
最小的斐波那契数大于或等于11是13。如图所示，fibMm2=5、fibMm1=8和fibM=13。
另一个实现细节是偏移量变量（初始化为零）。它标志着已经被淘汰的范围，从前面开始。我们将不定期更新它。
现在，由于offset值是一个索引，并且包括它和它下面的所有索引都已被消除，所以只需要向它添加一些东西。由于fibMm2标记了大约三分之一的数组，以及它标记的索引，肯定是有效的，我们可以将fibMm2添加到offset中，并检查索引i=min（offset+fibMm2，n）处的元素。