二叉搜索树
概念
二叉搜索树又称二叉排序树,它是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
模拟实现(非递归)
节点
template<class K, class V>struct BSTreeNode //节点{using Node = BSTreeNode<K, V>;Node* _left; //左节点Node* _right; //右节点K _key; //键V _value; //值BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key),_value(value){} //拷贝构造};
寻找
根据BSTree的特点,
- 比该节点的值大,就走到该节点右节点
- 比该节点的值小,就走到该节点左节点
插入
- 先寻找,有相同值则return false
- 插入,链接父节点和原来的子树
删除
没有孩子/一个孩子
对于这种情况,
- 当删除节点左边为空,就将该节点右边托付给父亲
- 右边为空,就将左边托付给父亲
所以对于删除叶子节点也可以归纳到这里面
两个孩子:替换法
找一个能替换删除节点的节点,交换值,转换删除替换节点
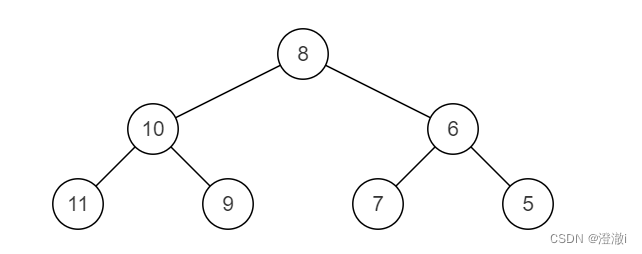
比如:删除图中3这个节点
我们可以将左子树的最大节点或者右子树的最左节点替换掉3
即左子树最右节点或者右子树最左节点
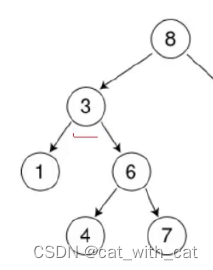
rightMin的问题
假如rightMinParent为空指针,那下面这句特殊情况会出错
rightMinParent->_left = rightMin->_right;
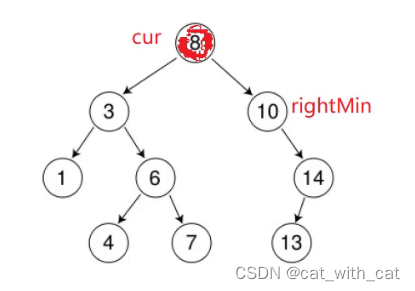
这幅图中,当删除根节点时,右子树最左节点为空,不进循环,rightMinParent为空,访问空节点的左子树会出现错误
代码
测试代码
void TestBSTree()
{BSTree<string, string> dict;dict.Insert("insert", "插入");dict.Insert("erase", "删除");dict.Insert("left", "左边");dict.Insert("string", "字符串");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << str << ":" << ret->_value << endl;}else{cout << "单词拼写错误" << endl;}}string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };// 统计水果出现的次BSTree<string, int> countTree;for (auto str : strs){auto ret = countTree.Find(str);if (ret == NULL){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();
}
完整代码
namespace key_value
{template<class K, class V>struct BSTreeNode //节点{using Node = BSTreeNode<K, V>;Node* _left; //左节点Node* _right; //右节点K _key; //键V _value; //值BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key),_value(value){} //拷贝构造};template<class K, class V>class BSTree{using Node = BSTreeNode<K, V>;public://插入bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}//如果树为空,特殊判断Node* parent = nullptr;//父节点//方便记录父节点原来的子树Node* cur = _root;while (cur != nullptr){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}//查找完再判断是父节点的左树还是右数//标记为Acur = new Node(key, value);if (parent->_key > key){parent->_right = cur;}else{parent->_right = cur;}return true;}//查找,并返回这个节点的指针(位置)Node* Find(const K& key){Node* cur = _root;while (cur != nullptr){if (cur->_key > key){cur = cur->_right;}else if (cur->_key < key){cur = cur->_left;}else{return cur;}}return nullptr;}//删除节点bool Erase(const K& key){//并没有在开头判断删除节点是否为根节点//而是在下面Node* parent = nullptr;Node* cur = _root;while (cur != nullptr){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{ //找到后进行判断if (cur->_left == nullptr){if (cur == _root)//对于删除根节点进行特判{_root = cur->_right;}else{ //功能Aif (cur == parent->_right){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}delete cur;return true;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->left;}else{ //功能Aif (cur == parent->_right){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}delete cur;return true;}else{// 采用右树最左节点替换法Node* rightMin = cur->_right;Node* rightMinParent = cur;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;if (rightMin == rightMinParent->_right){rightMinParent->_right = rightMin->_right;}else{rightMinParent->_left = rightMin->_left;}delete rightMin;return true;}}}return false;}void InOrder()//中序打印{_InOrder(_root);}//因为外部取不到_root//所以再套一层private:Node* _root = nullptr;void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);std::cout << root->_key << " ";_InOrder(root->_right);}};
}
结语
现在再来写BSTree感觉也不是很困难,希望对你有帮助,我们下次见
(补充一下,代码是不全的,BSTree() 和~BSTree()都没写,用的默认的)




![[C++基础学习-06]----C++指针详解](https://img-blog.csdnimg.cn/direct/ba7d3d958bb0454794ba1e37da3ef71f.png)