1.TimeGPT-1
思路:在来自不同领域的大量数据上训练模型,然后对未见过的数据产生零样本的推断。
作者对TimeGPT进行了超过1000亿个数据点的训练,这些数据点都来自开源的时间序列数据。该数据集涵盖了广泛的领域,从金融、经济和天气,到网络流量、能源和销售。
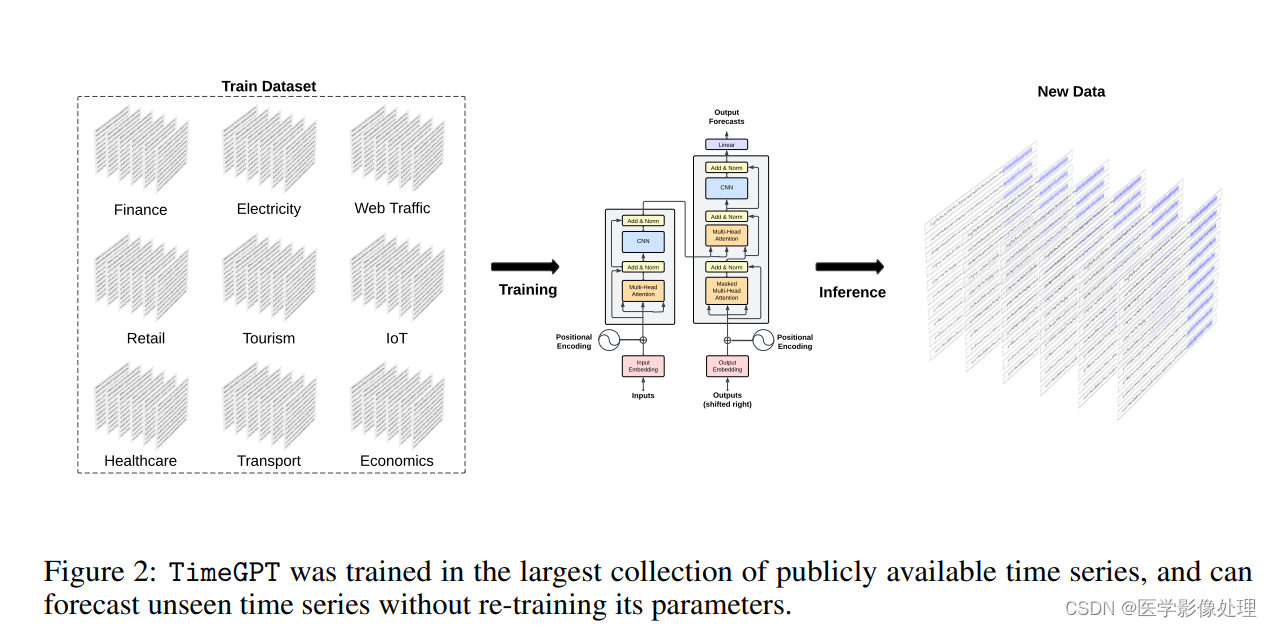
TimeGPT 是一个基于 Transformer 的时间序列模型,具有基于 [Vaswani et al., 2017] 的自注意力机制。 TimeGPT 采用历史值窗口来生成预测,并添加本地位置编码来丰富输入。该架构由多层编码器-解码器结构组成,每层都有残差连接和层归一化。最后,线性层将解码器的输出映射到预测窗口维度。一般的直觉是,基于注意力的机制能够捕获过去事件的多样性并正确推断未来潜在的分布。
TimeGPT模型结构:
- 架构基础:TimeGPT基于Transformer架构,使用自注意力机制,类似于在自然语言处理(NLP)中使用的模型。
- 输入:模型接受历史值窗口作为输入,并添加局部位置编码以丰富输入信息。
编码器-解码器结构:包含多层,每层都有残差连接和层归一化。 - 输出:最后,一个线性层将解码器的输出映射到预测窗口维度。
损失函数和评价指标:
- 损失函数:文章没有明确指出用于训练TimeGPT的具体损失函数,但通常时间序列预测模型会使用均方误差(MSE)或其变体作为损失函数。
- 评价指标:
相对平均绝对误差 (rMAE):用于衡量模型预测与实际值之间的误差,是平均绝对误差(MAE)与基线模型(如季节性天真模型)性能的比值。
相对均方根误差 (rRMSE):与rMAE类似,但基于均方根误差(RMSE)计算。 - 其他关键点:
训练数据集:TimeGPT在超过1000亿数据点的公开可用时间序列数据集上进行训练,涵盖金融、经济、医疗保健、天气等多个领域。
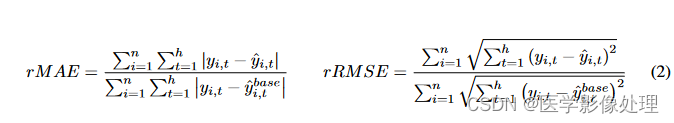
不确定性量化:
TimeGPT使用基于历史错误的一致性预测来估计预测区间,这有助于风险评估和决策制定。
零样本推断 (Zero-shot inference):TimeGPT能够在未经微调的情况下直接在新的预测任务上表现良好。
微调 (Fine-tuning):通过在特定任务的数据集上进一步训练,可以调整模型参数以适应新任务的需求。
https://blog.csdn.net/fengdu78/article/details/134301864
Chronos模型
注意:内容由kimi大模型生成,未做完全的校正,请辨别使用。
这篇文章介绍了一个名为Chronos的时间序列预测框架。Chronos利用了预训练的概率时间序列模型,并通过以下方式进行操作:
模型结构:
- Chronos通过缩放和量化将时间序列值转换为固定词汇表中的离散标记(tokens)。
- 它使用现有的基于Transformer的语言模型架构来训练这些标记化的时间序列,不需要对模型架构进行任何改变。
- Chronos选用了T5家族的变体作为其主要架构,这些变体的参数量从20M到710M不等。
损失函数:
- Chronos使用交叉熵损失函数来训练模型,该损失函数衡量的是量化的真实标签分布与模型预测分布之间的差异。
评价指标:
- 文章使用了加权分位数损失(WQL)来评估概率预测的质量,这是一种与连续排序概率分数(CRPS)相关的度量,常用于评估概率预测。
- 为了评估点预测性能,文章使用了平均绝对缩放误差(MASE),这是一种考虑了时间序列季节性的误差度量。
数据增强技术:
- Chronos结合了数据增强策略,包括TSMixup和KernelSynth,以增强训练数据的多样性,提高模型的鲁棒性和泛化能力。
- TSMixup通过随机采样基础时间序列,并基于它们进行凸组合来生成新的时间序列。
- KernelSynth使用高斯过程通过随机组合核函数来生成合成时间序列。
实验结果:
- Chronos在包含42个数据集的综合基准测试中表现出色,这些数据集既包括了训练语料库中的数据集,也包括了新的未见数据集。
- Chronos模型在训练语料库中的数据集上显著优于其他方法,在新的未见数据集上也展现出了可比性,甚至是更好的零样本(zero-shot)性能。
结论:
- Chronos证明了预训练的语言模型架构在时间序列预测任务上的有效性,即使是在没有特定于时间序列的设计或特征的情况下。
- Chronos作为一个通用的时间序列模型,其准确性和相对较小的模型尺寸使其成为零样本预测应用的首选工具。
- 通过进一步的微调,Chronos模型的性能还有望得到提升。
文章还讨论了Chronos的未来发展方向,包括扩展到多变量预测、考虑共变量的时间序列预测,以及其他时间序列分析任务。此外,文章还探讨了提高模型推理速度和处理更高频数据的可能性。最后,文章强调了高质量公共时间序列数据集的需求,以及合成数据生成方法的进步,这些对于发展和改进像Chronos这样的预训练模型至关重要。
回归函数评价指标
MSE均方误差
MSE(Mean Square Error):
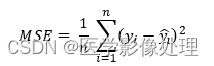
均方误差描述了样本真实值与预测值差方求和的平均值,在机器学习中,利用均方误差最小化优化模型的方法称为“最小二乘法”
RMSE
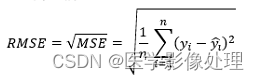
RMSE(Root Mean Square Error)即对MSE开平方根:
MAE平均绝对误差

MAE(Mean Absolute Erroe)即真实值与预测值差的绝对值和求平均:
带归一化的误差求解方法
MAPE
MAPE(Mean Absolute Percentage Error):
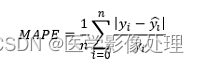
即求所有样本真实值与预测值差绝对值与真实值的比例的和求平均。
MSPE
MASE(Mean Scaled Percentage Error)平均平方百分比误差:
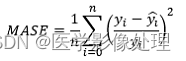
即求所有样本的真实值与预测值的差与真实值的比例求平方的和求平均。
MASE(chronos大模型中使用)
mean absolute scaled error (MASE, Hyndman & Koehler (2006))
平均绝对比例误差(Mean Absolute Scaled Error,简称MASE)是一种用于评估时间序列预测模型性能的指标。与其他误差指标不同,MASE 可以用于比较不同时间序列数据集的模型性能,因为它可以归一化误差值。
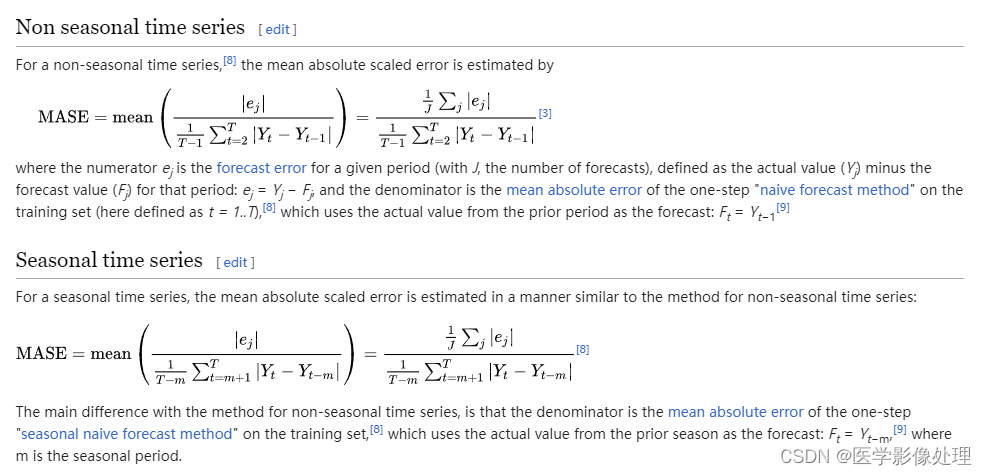
通常,MASE的值越小,表示预测的准确度越高。MASE的值可以为任何正实数,因此没有固定的范围或取值区间。
Mean squared scaled error (MSSE) or root mean squared scaled error (RMSSE).
sktime里有各种评价指标的实现。



参考
- Another look at measures of forecast accuracy 【推荐】
- https://www.sktime.net/en/latest/api_reference/auto_generated/sktime.performance_metrics.forecasting.mean_squared_scaled_error.html
- https://en.wikipedia.org/wiki/Mean_absolute_scaled_error
- https://blog.csdn.net/weixin_43786241/article/details/109626631
TILDE-Q:让时间序列预测结果更真实的损失函数
解决问题:常用的损失函数MSE、MAE是让预测结果与每个真实值的差距最小。所以训练的模型可能无法预测出准确的形状,而只是找到一种最简单的方法让点预测结果误差最小。
下述这篇文章为了解决这个问题,文中提出了一种新的时间序列预测损失函数,能够更加关注时间序列预测结果的形状和真实序列是否匹配,弥补了MSE等点误差损失函数的缺陷。
论文标题:TILDE-Q: A TRANSFORMATION INVARIANT LOSS FUNCTION FOR TIME-SERIES FORECASTING
下载地址:https://arxiv.org/pdf/2210.15050v1.pdf
源码:https://github.com/HyunWookL/TILDE-Q (备注:没太多人使用,目前效果存疑)
https://cloud.tencent.com/developer/article/2195702
相关性度量
MSE用来评估预测值与真值间误差的绝对值,但是无法度量相关性,因此常用PCC(皮尔逊相关)计算二者相关性作为补充的评价指标。
CCC则既能够体现相关性(趋势),又能够体现误差值。
一致性相关系数Concordance Correlation Coefficient
CCC结合了MSE和PCC的特点,提供了一种可以同时度量相关性和绝对插值的指标,具体定义如下:
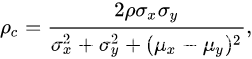
其中
ρ表示相关系数。绝对差值越小,CCC值越大,相关性越强CCC值也越大,因此该值越接近1,则算法的表现越好。
有个疑问,PCC可以作为回归的衡量指标吗?
个人思考:PCC主要是衡量两个变量之间的线性相关,如果使用这个,仅能去评价预测值和真实值的线性相关性,但无法去衡量预测值与真实值之间实际的差异还有多少,即无法学习或者衡量真实分布的量纲。
而且,PCC也不是衡量分布一致性的指标,常常衡量两个概率分布之间的差异性指标有:KL(Kullback-Leibler divergence)散度、JS(Jensen-Shannon divergence)散度、交叉熵(cross entropy)、Wasserstein距离等。
参考:
https://blog.csdn.net/Avery123123/article/details/102681688
https://en.wikipedia.org/wiki/Concordance_correlation_coefficient
https://www.cnblogs.com/duduheihei/articles/14088547.html