在深度学习的世界中,计算图扮演着至关重要的角色。它不仅是数学计算的图形化表示,更是链式求导与反向传播算法的核心。本文将深入探讨计算图的基本概念、与链式求导的紧密关系及其在反向传播中的应用,旨在为读者提供一个全面而深入的理解。
计算图的基本概念
计算图(Computational Graph)是一种用于描述数学计算过程的图形模型。在计算图中,节点代表数学运算或变量,边代表运算结果之间的依赖关系。这种有向无环图的结构使得复杂的计算过程变得直观且易于理解。通过将神经网络和损失函数连接成一个计算图,我们可以清晰地看到输入、输出和参数之间的依赖关系,为后续的链式求导和反向传播提供了坚实的基础。
链式求导与计算图的关系
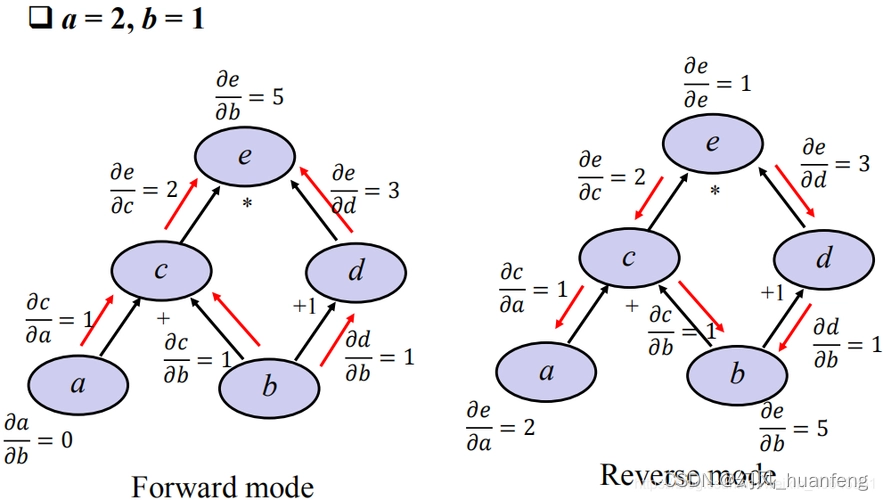
链式求导(Chain Rule)是微积分中的一个基本法则,用于计算复合函数的导数。在计算图中,链式求导表现为一种从输出节点到输入节点的反向传播过程。具体来说,当我们需要计算某个输出节点关于某个输入节点的导数时,可以沿着计算图中的边反向追溯,利用链式求导法则将问题分解为一系列子问题的求解。这种分治策略使得复杂的导数计算变得高效且易于实现。
链式求导与计算图之间的紧密关系体现在以下几个方面:
- 计算图提供了链式求导的直观表示。在计算图中,我们可以清晰地看到每个节点之间的依赖关系,从而方便地应用链式求导法则。
- 计算图简化了链式求导的计算过程。通过将复杂的计算过程分解为一系列简单的子问题,我们可以降低计算难度并提高计算效率。
- 计算图支持高效的反向传播算法。在反向传播过程中,我们可以利用计算图中存储的中间结果来加速计算过程,从而进一步提高算法的效率。
反向传播中的计算图应用
反向传播(Backpropagation)是深度学习中的一项关键技术,用于计算损失函数关于网络参数的梯度并更新网络参数。在计算图中,反向传播表现为一种从输出节点到输入节点的反向遍历过程。具体来说,反向传播算法通过以下步骤实现:
- 前向传播:首先,我们沿着计算图中的边进行前向遍历,计算每个节点的输出值并存储中间结果。这个过程对应于神经网络的前向传播过程。
- 计算损失:然后,我们根据输出节点的输出值和真实值计算损失函数的值。这个损失值将作为后续反向传播的起点。
- 反向传播:接下来,我们从输出节点开始反向遍历计算图,利用链式求导法则计算每个节点关于损失函数的梯度值。这个过程对应于神经网络的反向传播过程。
- 更新参数:最后,我们根据计算得到的梯度值更新网络参数的值。这个过程是神经网络学习的关键步骤之一。
在计算图中应用反向传播算法具有以下优点:
- 直观性:计算图提供了一种直观的表示方式,使得反向传播过程变得易于理解和实现。
- 高效性:通过利用计算图中存储的中间结果,我们可以加速反向传播过程并提高算法的效率。
- 灵活性:计算图可以支持各种复杂的神经网络结构和损失函数形式,使得深度学习算法具有更强的灵活性和可扩展性。