一、插入排序
1、直接插入排序
核心思想:把后一个数插入到前面的有序区间,使得整体有序
思路:先取出数组中第一个值,然后再用tmp逐渐取出数组后面的值,与前面的值进行比较,假如我们进行的是升序排序,那么此时前面排序好的数组中,最后一个值最大,如果tmp大于它,就插入后面,否则end -- 往前走,进行比较,(注意:此时数组也要往后赋值),找到比它小的元素,则插在那个元素后面即可,如果直到为0的时候,仍然小于,则把它放在下标为0的位置。
最坏情况(数组元素逆序):每次插入,元素都要往后移动
- 移动次数:1 +2 +3…+ n => 等差数列 ==>O(N^2)
最好情况:(接近有序或者有序),基本不用移动数据 ->O(N)、
稳定性:稳定
- 将x插入到
[0,end]的有序区间的时候,当区间元素和x的值相同的时候,是将x插入到该区间元素后面,二者的相对顺序不变
图文演示:假如a[ 5 ] = {3 , 2, 1, 4, 5}

代码演示:
//插排二
//时间复杂度 O(N^2)
// 最坏情况 :逆序
// 最好情况: 顺序或者接近有序 O(N)
void InsertSort(int* a, int n) //n表示数组有多少个元素
{for (int i = 0; i < n - 1; i++) //只需要走n-1个元素即可,防止越界{int end = i; //后面下标int tmp = a[end + 1]; //存下后面的值while (end >= 0) //与前面下标元素进行比较{if (a[end] > tmp) { //待插入元素小于前面元素,则数组往后走一位a[end + 1] = a[end];end--;}else break; //找到比待插入元素小的}a[end + 1] = tmp; //插入当前位置}
}2、希尔排序
核心思想:
1.先选定一个gap,把待排序数据分组,所有距离为gap分在同一组内,并对每一组内的记录进行排序。
预排序:目的是让数组更接近于有序,这样子后续gap为1进行直接插入排序,效率就是O(N)
2.然后取重复上述分组和排序的工作,当到达gap=1时,就是直接插入排序,整体就有序了
- gap越大:预排序越快,预排序后越不接近有序
- gap越小:预排序越慢,预排序后越接近有序。
- 数据是逆序的时候,预排序完成就接近有序,此时预排序的效果最好。
图文演示:

时间复杂度:O(N^1.3)
稳定性:不稳定
- 相同的值,预排序时可能分到不同的组里面,导致相对顺序发生改变
写法1:多组进行排序
//多组一起进行预排序
void Shellsort1(int* a, int n)
{//int gap = 1; //如果gap为1 则为插入排序//把间隔为gap的数组同时排int gap = n;while (gap > 1){gap /= 2; //gap>1 都是预排序 接近有序//gap=gap/3+1;for (int i = 0; i < n - gap; i++)//注意:i的范围! 否则end+gap会越界{int end = i;//end的范围:[0,n- gap -1]int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];//把a[end]往后移动,以gap为间隔的为一组,所以移动到a[end+gap]位置end -= gap;//下一轮循环,以gap为间隔的为一组,前一个数(end-gap位置对应的值)和 tmp 比较}else break;}a[end + gap] = tmp;}}
}写法2:每一组分别进行预排序
每一组都进行预排序
- 一次只排序间隔为gap的元素(同组元素),一共有gap组,所以要循环gap次
需要变动的位置:循环gap次,每次处理一组!
- 每一组的起始位置是当前组的组号,然后每次变化范围:
gap
//多组一起进行预排序
void Shellsort2(int* a, int n)
{//int gap = 1; //如果gap为1 则为插入排序//把间隔为gap的数组同时排int gap = n;while (gap > 1){//目的是为了保证最后能让gap为1,进行直接插入排序gap /= 2; //gap>1 都是预排序 接近有序//gap=gap/3+1;for (int j = 0; j < gap; j++) {for (int i = j; i < n - gap; i += gap)//注意:i的初始值!!和变动范围 i+=gap{int end = i;//end的范围:[0,n- gap -1]int tmp = a[end + gap];//下一轮循环,以gap为间隔的为一组,前一个数(end-gap位置对应的值)和 tmp 比较while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;//以gap为间隔的为一组,把tmp放在end + gap位置 }}}
}二、选择排序
1、直接选择排序
核心思想:第一次从R[0]~R[n-1]中选取最小值,与R[0]交换,第二次从R[1]~R[n-1]中选取最小值,与R[1]交换,....,第i次从R[i-1]~R[n-1]中选取最小值,与R[i-1]交换,.....,第n-1次从R[n-2]~R[n-1]中选取最小值,与R[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
时间复杂度:遍历一遍才能选出一个数或者两个数,无论什么情况都是O(N^2)。
稳定性:不稳定
- 在区间当中找到最大和最小的数和区间左右端点位置的值交换,可能会导致两个相同的值相对顺序发生变化
图文演示: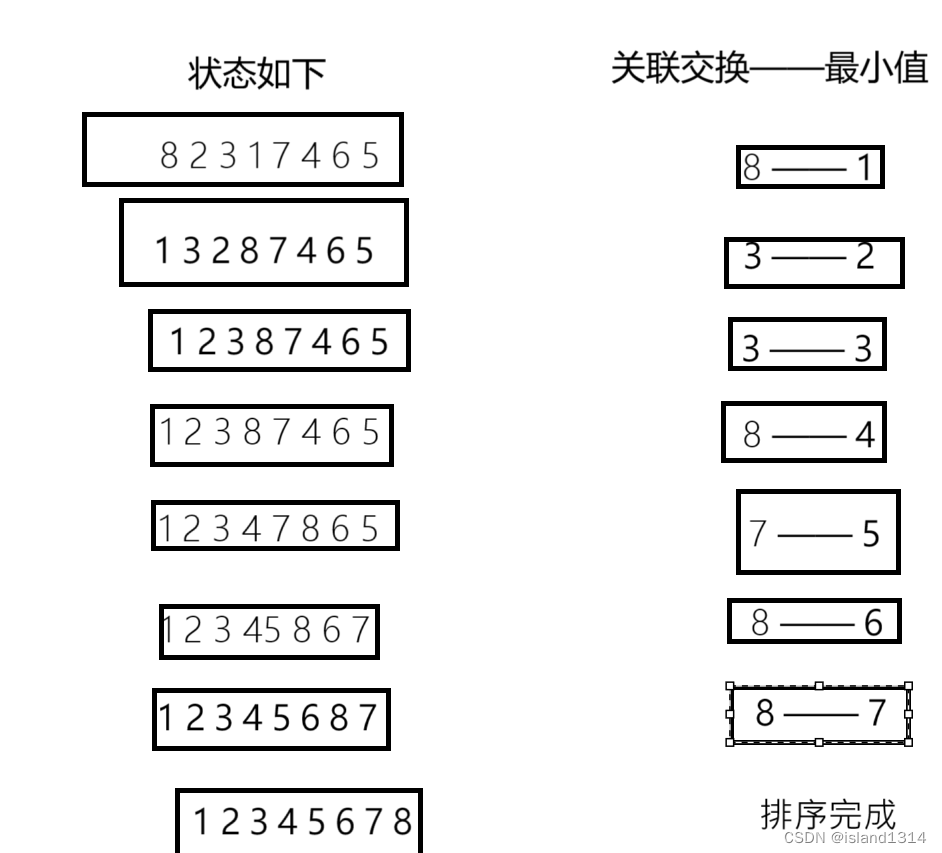
代码演示:
方法一:每次选择一个数,比如一个移动范围内的最小值
//直接选择排序
//写法1:每次选择一个数
void SelectSort1(int* a, int n)
{int begin = 0;while (begin < n - 1) {//当区间只有一个元素就不需要选了所以循环条件为:end > 0int mini = begin;for (int i = begin + 1; i < n; i++) {// 在[begin, n-1]中选取最小值if (a[mini] > a[i]) mini = i;}swap(a[begin], a[mini]);begin++;}
}方法2:每次选择两个数
思路:每次从要排序的区间当中找到最大和最小的数,如果是排序,那么把他区间的最大的数和区间右端点对应值交换,把区间中最小的数和区间左端点对应值交换,然后缩小区间重复上述步骤,直到区间只有一个数。
//写法2:每次选择两个数
void SelectSort2(int* a, int n)
{int begin = 0, end = n - 1;while (begin <end){int mini = begin, maxi = end;for (int i = begin; i <= end; i++){if (a[i] < a[mini]) mini = i; //找出最小的值下标if (a[i] > a[maxi]) maxi = i; //找出最大的值下标}swap(a[begin], a[mini]);//最小值放到begin位置//注意:如果begin和maxi一样,即begin就是最大值的位置//因为下面一步begin位置和值已经和mini位置交换了,所以就导致了mini位置放的才是最大值了//所以需要特判一下,如果begin和maxi相同,那么经过上面一步交换之后,mini位置放的才是最大值if (begin == maxi) maxi = mini;//加以优化,避免最大的数出现在第一个swap(a[end], a[maxi]);//最大值放到end位置begin++, end--; //缩小区间}
}2、堆排序
核心思想:
1.首先需要先建堆,只需要从最后一个叶子结点的父节点开始,在数组当中从后往前去向下调整即可共n个元素。
- 共n个元素,最后一个结点的下标为: n -1
- 它的父亲结点的下标为:parent = (child - 1)/2 = (n - 1- 1)/2
2.建好堆之后,将堆顶数据与堆的最后一个数据交换,然后对根位置进行一次堆的向下调整,但是调整时被交换到最后的那个数不参与向下调整,然后缩小堆中有效数据个数,剩下的元素进行向下调整,其余数又成一个大堆…重复上述步骤,直到堆中只剩下一个元素。
注意:
a、排升序建大堆
b、排降序建小堆
对于N个元素建堆,我们用筛选法建堆,从 N/2 (即最后一个非叶子节点)的元素开始建堆
时间复杂度分析:无论哪种方法建堆:都是O(N*logN)
- 建堆的时间复杂度 + 调堆的时间复杂度 N*logN
稳定性:不稳定
- 在调堆的时候,可能会导致相同元素的相对顺序改变
图文演示:
代码演示:
//排升序最后是建大堆
void AdjustDwon(int* a, int n, int root)
{int parent = root;int child = parent * 2 + 1; //默认是左孩子,右孩子比左孩子大1while (child < n){//1、选出左右孩子中大的那一个if (child+1<n && a[child + 1] > a[child]) //建一个大堆{child += 1;}//2、然后再与父亲比较,若比父亲大就发生交换if (a[child] > a[parent])//让父亲永远大于儿子{Swap(&a[child], &a[parent]);parent = child; //交换下标child = parent * 2 + 1;}else break; //记得跳出循环}
}//第一个和最后一个交换,把它不看作堆里面,前n-1个数向下调整,选出次大的数,再跟倒数第二个位置交换
void HeapSort(int* a, int n)
{//把数组建成大堆for (int i = (n-1-1) / 2; i >= 0; i--) //筛选法选出最后一个非叶子节点{AdjustDwon(a, n, i); //建大根堆}int end = n - 1;while (end > 0)//开始向下调整{Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);--end;}
}举例:将整数数组(7-6-3-5-4-1-2)按照堆排序的方式原地进行升序排列,请问在整个排序过程中,数组的顺序是_____。(6-5-3-2-4-1-7)

三、交换排序
1、冒泡排序
核心思想:重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行,直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
- n个元素,只需排序n-1次,就可以让n个数有序
优化:如果提前有序了(某一趟冒泡当中没有元素交换),就不需要再冒泡了。
时间复杂度:
- 最坏情况:第一轮:N个数比较交换,第二轮:N-1个数比较交换… ,此时相当于是等差数列,复杂度为O(N^2)
- 最好情况:数组接近有序/有序,某一趟冒泡当中没有元素交换直接结束,O(N)
稳定性:稳定
- 相邻元素进行比较,相同的元素之间不进行交换
void BubbleSort(int* a, int n)
{
//每一趟可以确定一个元素到准确位置,n个元素只需要进行n-1趟for (int i = 0; i < n - 1; i++) {bool flag = 0;
//每一趟都可以少比较一个已经确定好的数for (int j = 0; j < n - 1 - i; j++){if (a[j] > a[j + 1]) {swap(a[j], a[j + 1]);flag = 1;}}if (flag == 0) break; //说明没有进行交换,此时已经有序,跳出即可}
}2、快速排序
快速排序是基于 分治法 的一个排序算法。
核心思想:取待排序区间上的某一个元素作为基准值,根据处理方法,将待排序区间上的元素划分为:左区间的元素小于基准值,右区间的元素大于基准值,然后对左右区间重复这个过程,直到所有元素都排列在相应位置上为止
代码演示:
最简便模板:(记住这个即可)
void QuickSort(int q[], int l, int r) //先分治再递归
{if (l >= r) return; //递归截止条件int x = q[l + r >> 1]; // 但是一般选择第一个或者最后一个int i = l - 1, j = r + 1; //注意:l-1 和 r + 1while (i < j)//x左边都是小于x的,右边都是大于x的 {do i++; while (q[i] < x);do j--; while (q[j] > x);//假设上面截止时且满足i < j,此时a[i] >= x, a[j] <= x if (i < j) swap(q[i], q[j]);}QuickSort(q, l, j);QuickSort(q, j + 1, r);
}比如快速排序的第一趟结果:
比如关键字(20,15,14,18,21,36,40,10)以20为基准进行排序。
第一步,先从后往前找出小于基准数20的数,并与基准数20交换得:10,15,14,18,21,36,40,20)。
第二步,再从前往后找出大于基准数20的数,并与基准数20交换得:10,15,14,18,20,36,40,21)。
再一次执行第一步与第二步,直到最后基准数左边的序列都小于基准数,基准数右边的序列都大于基准数。
所得结果:(10,15,14,18,20,36,40,21)。为第一趟排序的结果。
四、归并排序
核心思想:根据左右区间的值,计算一个中间值mid,先让[left,mid] [mid+1,right]两个区间有序, 然后这两个有序区间进行归并 (归并到临时数组),将临时数组的内容拷贝回去。
时间复杂度:O(N*logN)
空间复杂度:O(N)
稳定性:稳定
- 归并的时候,相同的值,先拷贝左区间的值,再拷贝右区间的
归并操作,也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1。
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11;
逆序数为14;(因此我们可以用 归并算法 来计算逆序数)
代码演示:
const int N = 10010;
int tmp[N];
void merge_sort(int q[], int l, int r) //先归并再分治
{if (l >= r) return; //递归截止int mid = l + r >> 1; //记录中间值merge_sort(q, l, mid); merge_sort(q, mid + 1, r);int k = 0, i = l, j = mid + 1; //k表示tmp储存的元素数量while (i<=mid && j<=r) //注意下面都是<=,保证了它的稳定性{if (q[i] <= q[j])tmp[k++] = q[i++]; else tmp[k++] = q[j++];}//防止分布不均while (i <= mid) tmp[k++] = q[i++];while (j <= r) tmp[k++] = q[j++]; //注意i的范围是[l,r] for (i = l, j = 0; i <= r; i++,j++) q[i] = tmp[j]; //拷贝}五、计数排序——鸽巢原理
核心思想:统计相同元素出现次数,根据统计的结果将序列写回到原来的序列中
统计每个数据出现的次数 count[a[i]]++
适合数据集中的数组进行排序
时间复杂度O(N+range)
空间复杂度 O(range)稳定性:不稳定
- 计数到count数组中,每个元素已经没有顺序了
void CountSort(int* a, int n)
{int max = a[0], min = a[0];for (int i = 0; i < n; ++i){if (a[i] > max)max = a[i]; //找出最大值if (a[i] < min)min = a[i]; // 找出最小值 }int range = max - min + 1; //比如109 100 实际有10个值int* count = (int*)malloc(sizeof(int) * range);//数组元素进行映射。此时x元素映射在x - min位置memset(count, 0, sizeof(int) * range);for (int i = 0; i < n; ++i){count[a[i] - min]++;}//将count数组的内容映射回去原数组,此时对应的值为i + minint j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}free(count);
}上述八大排序的稳定性以及复杂度
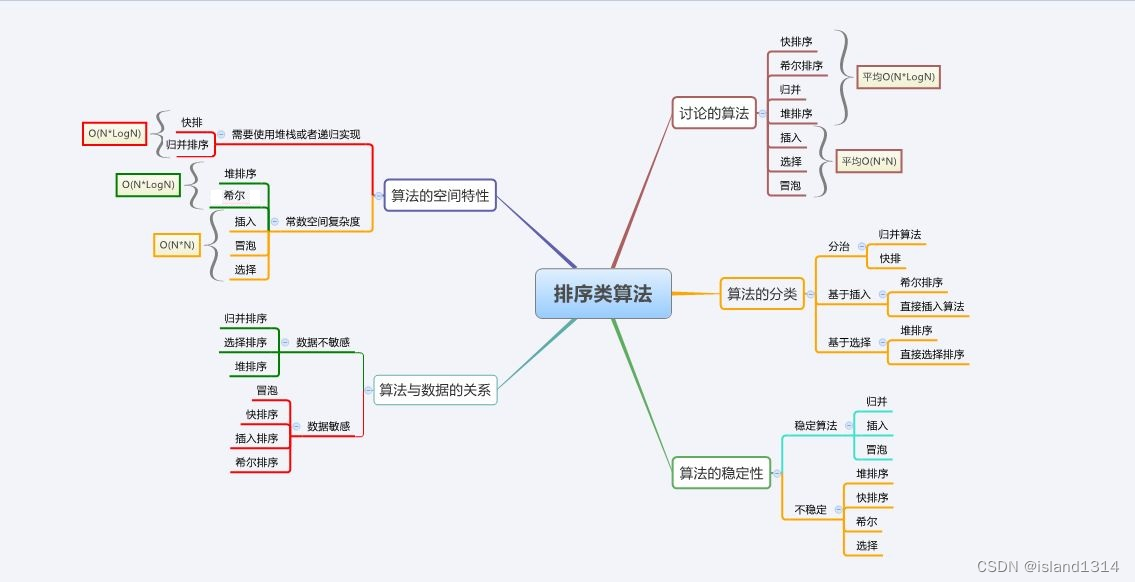
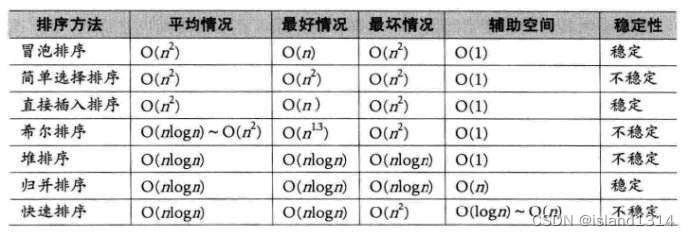
注意:
1、对于快速排序:如果加了三数取中 + 三路归并 最坏就不是O(N^2)
2、为了绝对的速度选快排,为了省空间选堆排,为了稳定性选归并
3、时间复杂度:O(N*logN),额外空间复杂度低于O(N),且稳定的基于比较的排序是不存在的
最后下面我们再提一个排序
九、基数排序
代码演示:
bool check(int* arr, int l, int r)
{for (int i = l + 1; i < r; i++){if (arr[i] < arr[i - 1]) return true;}return false;
}// 扩大范围 从 0 - 99为基数
void radix_sort(int* arr, int l, int r)
{
#define K 65536int* cnt = (int*)malloc(sizeof(int) * K);int* temp = (int*)malloc(sizeof(int) * (r - l));// round 1memset(cnt, 0, sizeof(int) * K);for (int i = l; i < r; i++) cnt[arr[i] % K] += 1; //求前缀和for (int i = 1; i < K; i++) cnt[i] += cnt[i - 1];for (int i = r - 1; i >= l; i--) temp[--cnt[arr[i] % K]] = arr[i]; //记录当前数字应该存放的位置memcpy(arr + l, temp, sizeof(int) * (r - l));// round 2memset(cnt, 0, sizeof(int) * K);for (int i = l; i < r; i++) cnt[arr[i] / K] += 1; //求前缀和for (int i = 1; i < K; i++) cnt[i] += cnt[i - 1];for (int i = r - 1; i >= l; i--) temp[--cnt[arr[i] / K]] = arr[i]; //记录当前数字应该存放的位置memcpy(arr + l, temp, sizeof(int) * (r - l));}







![[图解]DDD架构好简单我学会了-学会也没啥用](https://img-blog.csdnimg.cn/direct/9016e93f426d41dd8c1668e4e0f5bdb5.png)