快速排序(java细节实现)

快速排序:

Hoare版:

挖坑法

快速排序的优化

快速排序的非递归实现

小结

从小到大排序

快速排序:

基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

简单来说就是给定一个数组:

选取其中的一个数,以这一个数为分界线, 左边都比这个数小, 右边都比这个数大, 然后分为左边和右边的两组再次进行重复操作. 直到这组数只有一个, 听起来麻烦, 实则简单, 重点是找到区间的基准值, 就是找到作为每一组分界线的那个数.

将区间按照基准值划分为左右两半部分的常见方式有：Hoare版和挖坑法.

Hoare版:

选取第一个数A作为分界线, 然后右边从后往前进行遍历, 如果这个数B小于A那么停下来, 然后左边从A后便开始遍历, 如果这个数C大于A停下来, C和A进行交换, 然后重复上述操作, 知道B和C相遇,(B和C指两边正在走的数字), 相遇之后和第一个数字进行交换位置, 得到以交换后的数字为分界线的左右两组数据. 最后在让左右两组数据重复以上操作.

代码实现:

    /*** 快速排序* 时间复杂度: 最好: O(N*logN)*            最坏:O(N^2)* 空间复杂度:最好:O(logN)*           最坏:O(N)* @param array*/public static void quickSort(int[] array) {quick(array, 0, array.length-1);}private static void quick(int[] array, int start, int end) {if (start > end) {return;}int pivot = partitionHoare(array, start, end);quick(array, start, pivot-1);quick(array, pivot+1, end);}private static int partitionHoare(int[] array, int left, int right) {int tmp = array[left];int i = left;while(left < right) {while(left < right && array[right] >= tmp) {right--;}while(left < right && array[left] <= tmp) {left++;}swap(array, left, right);}swap(array, left, i);return left;}public static void swap(int[] array, int i, int j) {int temp = array[i];array[i] = array[j];array[j] = temp;}

易错点:

1> 判断什么时候停止递归, 当start > end的时候. 这个条件的上一个是: end = start+1;

递归时可能交换也可能不交换, 如图所示用 left 和 right 替换start 和 end , 这次递归之后排序完成之后, start > end, 本次左边的递归结束, 然后开始右边的递归, 最后停止.

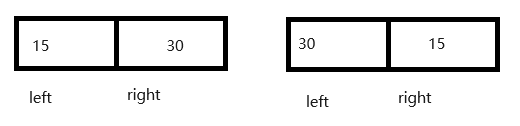
2> 在partitionHoare函数中, 在循环条件里面, 需要注意在里面循环也需要增加left < right的条件,假如没有这个条件,那么会出现如下图的情况: 这时候right越来越小, 然后right小于0了, 数组越界报错, 要注意里面循环的条件也要遵循外层循环. 并且left < right 要写在前面

3> 在partitionHoare函数中, 在循环条件里面, 注意为什么当array[i] == tmp时也需要right--或者left++, 因为这样的话才能让循环进行下去, 否则会当值陷入死循环.

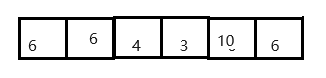
举个例子: 如图下图, 如果==跳出循环的话, 6和6进行交换之后会一直进行这个操作.

4> 为什么需要从右边开始比较移动数据呢. 如果从左边开始会出现什么情况呢?

举个例子:

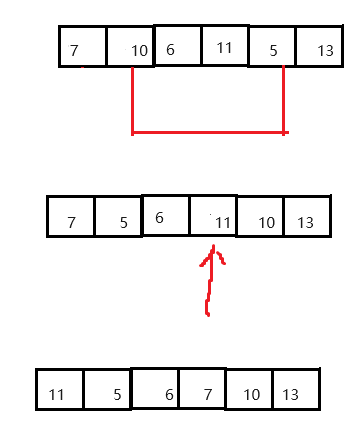
而我们选择先从右边筛选数据的结果则是正确的.

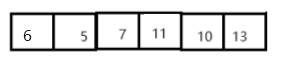
这就是为什么必须一定要从右边开始进行选择的原因, 就是为了尽量让这个数停在靠左的位置, 把比较大的数放在右边.

挖坑法

原理都差不多, 挖坑法选择了一个数作为基准, 然后挖出这个数A, 然后从左边选择比A小的数B,将B填入坑中, 然后从左边挖出比A大的数C放在右边的坑上,最后当遇到坑后直接将A填入坑中.

        /*** 快速排序* 时间复杂度: 最好: O(N*logN)*            最坏:O(N^2)* 空间复杂度:最好:O(logN)*           最坏:O(N)* @param array*/public static void quickSort(int[] array) {quick(array,0,array.length-1);}private static void quick(int[] array, int start, int end) {if(start >= end) {return;}int pivot = partitionHole(array,start,end);quick(array, start,pivot-1);quick(array, pivot+1,end);}/*** 挖洞快速排序* @param array* @param left* @param right* @return*/private static int partitionHole(int[] array, int left, int right) {int tmp = array[left];while(right>left) {//单独的循环不能一直减到超过最左边的边界while(right > left && array[right] >= tmp) {right--;}array[left] = array[right];while(right > left && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}public static void swap(int[] array, int i, int j) {int temp = array[i];array[i] = array[j];array[j] = temp;}

快速排序的优化

接下来讲一下快速排序的优化.为什么需要优化呢, 因为一组数据如果是逆序或者正序的话, 会出现类似于一个树只有一边的情况, 这样会让栈可能挤爆,我们优化目的让递归次数减少的多一点,然后让每一次分割尽量平均一点.

三数取中法(降低了树的高度)

举个例子:

这个时候我们正常情况下选择1作为key基准值, 最后它的右子树会很高,

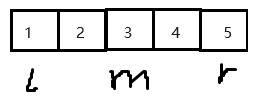
现在我们选择这个数组之后找到其中的left, right, mid三个数据中第二小的, 这样的话分为左右两组, 平均了左右树的高度.我们如何找到一个中位数呢.往下看.

我们得到了一组数据的下标, 然后分为几种情况L下标的值大与R下标的值,

我们判断M中间下标的值分为三种情况, 比L大, 或比R小, 或其他(L和R之间).

很容易理解.

代码实现如下:

    /*** 快速排序优化* 少于一定数时用插入排序* 选择更靠中间的key*/private static int middleNum(int[] array, int left, int right)  {int mid = (left + right) / 2;if(array[left] < array[right]){if(array[mid] > array[right]) {return right;}else if(array[mid] < array[left]) {return left;}else {return mid;}}else {if(array[mid] < array[right]) {return right;}else if(array[mid] > array[left]) {return left;}else {return mid;}}}

这个实现之后, 当我们进行分组到一定层次后, 可以用直接插入的方法减少递归次数, 当分的组数很多时, 越往下越多, 然后最后几组的数据较少, 用直接插入的方法会在一定程度上减少递归次数, 加快运算速度.

最后代码实现如下:

    /*** 快速排序* 时间复杂度: 最好: O(N*logN)*            最坏:O(N^2)* 空间复杂度:最好:O(logN)*           最坏:O(N)* @param array*/public static void quickSort(int[] array) {quick(array,0,array.length-1);}private static void quick(int[] array, int start, int end) {if(start >= end) {return;}if(end - start+1<=15) {insertSort(array, start, end);return;}int index = middleNum(array, start, end);swap(array, index, start);int pivot = partitionHole(array,start,end);quick(array, start,pivot-1);quick(array, pivot+1,end);}public static void insertSort(int[] array, int left, int right) {for(int i = 1+left; i <= right; i++) {int j = i-1;int tmp = array[i];for (;j>=left;j--) {if(tmp < array[j]) {array[j+1] = array[j];}else {break;}}array[j+1] =tmp;}}/*** Hoare版实现* @param array* @param left* @param right* @return*/private static int partitionHoare(int[] array, int left, int right) {int tmp = array[left];int i = left;while(right>left) {//单独的循环不能一直减到超过最左边的边界while(right > left && array[right] >= tmp) {right--;}while(right > left && array[left] <= tmp) {left++;}swap(array,left,right);}swap(array, i, left);return left;}/*** 挖洞快速排序* @param array* @param left* @param right* @return*/private static int partitionHole(int[] array, int left, int right) {int tmp = array[left];while(right>left) {//单独的循环不能一直减到超过最左边的边界while(right > left && array[right] >= tmp) {right--;}array[left] = array[right];while(right > left && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}/*** 快速排序优化* 少于一定数时用插入排序* 选择更靠中间的key*/private static int middleNum(int[] array, int left, int right)  {int mid = (left + right) / 2;if(array[left] < array[right]){if(array[mid] > array[right]) {return right;}else if(array[mid] < array[left]) {return left;}else {return mid;}}else {if(array[mid] < array[right]) {return right;}else if(array[mid] > array[left]) {return left;}else {return mid;}}}

快速排序的非递归实现

给定一组数据, 先第一次找到pivot的值, 然后建立一个栈, 先判断每一边的数是不是大于一个,(如何判断, pivot+1 < e 右边元素大于一个, pivot - 1 > s 左边元素大于一个) ,如果大于一个, 把左边数据的left 和 right放入栈中, 然后再把右边数据的left 和 right放入栈中,反之不放入数据.

然后判断栈空不空, 不空取出两个数r,l

然后进行第二次调用partition方法来寻找pivot基准值, 然后将每组数据的下标放到栈以此类推.

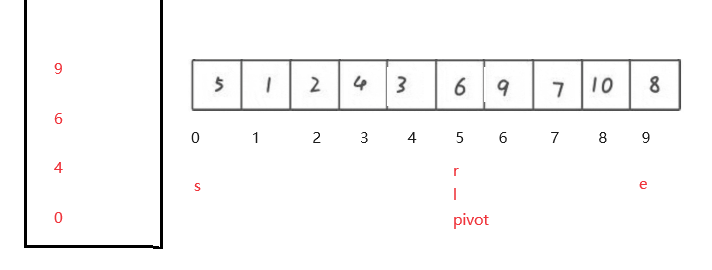
步骤:

1> 调用partiton方法找到pivot

2> 左边有没有两个元素, 有的话放到栈中

3> 右边同理

4> 如果栈不空的话, 取出r 和 l

代码实现

    /*** 快速排序的非递归实现* @param array*/public static void quickSortNor(int[] array) {int start = 0;int end = array.length-1;Stack<Integer> stack = new Stack<>();int pivot = partitionHoare(array, start, end);if(pivot-1>start) {stack.push(start);stack.push(pivot-1);}if(pivot+1<end) {stack.push(pivot+1);stack.push(end);}while(!stack.isEmpty()) {end = stack.pop();start = stack.pop();pivot = partitionHoare(array, start, end);if(pivot-1>start) {stack.push(start);stack.push(pivot-1);}if(pivot+1<end) {stack.push(pivot+1);stack.push(end);}}}/*** Hoare版实现* @param array* @param left* @param right* @return*/private static int partitionHoare(int[] array, int left, int right) {int tmp = array[left];int i = left;while(right>left) {//单独的循环不能一直减到超过最左边的边界while(right > left && array[right] >= tmp) {right--;}while(right > left && array[left] <= tmp) {left++;}swap(array,left,right);}swap(array, i, left);return left;}