一.堆的概念

1.堆的基本概念

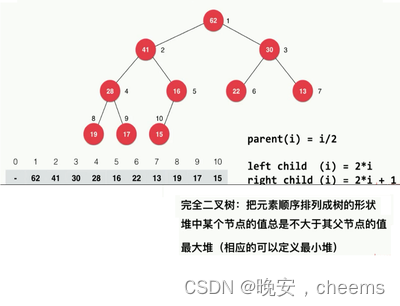
在计算机科学中，堆是一种特殊的数据结构，通常用于实现优先队列和动态分配内存。

2.堆的特征

堆是一个完全二叉树，它具有以下两个主要特性：

1. 堆序性：对于最大堆，在堆中的任意节点i，其父节点的值大于等于节点i的值；对于最小堆，在堆中的任意节点i，其父节点的值小于等于节点i的值。这意味着在最大堆中，根节点是堆中最大的元素；在最小堆中，根节点是堆中最小的元素。

2. 完全二叉树性质：除了最底层外，堆的其他层都是满的，并且最底层的节点集中在左侧。

3.堆的性质

根据堆序性质，我们可以高效地找到堆中的最大（最小）元素。这使得堆非常适用于解决一些需要高效获取最大（最小）元素的问题，例如优先队列和排序算法（如堆排序）。

堆可以用数组来实现，其中父节点和子节点之间的关系可以通过索引计算得出。通常，堆的插入和删除操作会触发堆的调整，以维持堆序性质。

需要注意的是，堆和操作系统中的堆内存分配是不同的概念。在操作系统中，堆内存指的是动态分配的内存区域，而在数据结构中，堆是一种数据结构。

4.堆的优缺点

优点：

1. 高效的插入和删除操作：在堆中，插入和删除元素的时间复杂度为O(log n)，其中n是堆中元素的个数。这是由于堆的调整过程只需要对树的高度进行操作，堆的高度通常比较小。

2. 快速获取最大（最小）元素：在最大堆中，根节点是堆中的最大元素；在最小堆中，根节点是堆中的最小元素。因此，可以在O(1)的时间复杂度内获取最大（最小）元素。

3. 实现优先队列：堆常用于实现优先队列，其中元素按照优先级进行排序。优先队列可以在O(1)的时间复杂度内获取最高优先级的元素，并且在O(log n)的时间复杂度内插入和删除元素。

缺点：

1. 不支持快速查找：堆并不提供快速查找指定元素的功能。如果需要在堆中进行查找操作，时间复杂度为O(n)，需要遍历整个堆。

2. 内存空间的浪费：堆使用数组来存储元素，如果事先不知道元素的个数，需要预分配一个较大的数组空间。这可能会导致内存空间的浪费。

3. 不稳定性：堆排序算法是一种不稳定的排序算法。在排序过程中，相等元素的相对顺序可能会改变。

二.堆的功能

1. 插入元素：向堆中插入一个新元素。插入操作会根据堆的特性进行调整，以保持堆的性质。

2. 删除最大（最小）元素：从堆中删除并返回最大（最小）元素。删除操作会将堆的最后一个元素移到堆顶，并根据堆的特性进行调整，以保持堆的性质。

3. 获取最大（最小）元素：返回堆中的最大（最小）元素，而不删除它。获取操作只是简单地返回堆的根节点的值。

4. 堆排序：使用堆进行排序。堆排序是一种基于堆的排序算法，它利用堆的性质进行排序操作。

5. 构建堆：将一个无序的数组转换为一个堆。构建堆的过程会进行堆调整，以满足堆的性质。

6. 堆化：对一个已有的堆进行调整，以满足堆的性质。堆化可以通过自上而下或自下而上的方式进行。

7. 堆的合并：将两个堆合并为一个堆。堆的合并操作通常用于合并多个优先队列。

8. 查找元素：在堆中查找指定元素。由于堆并不提供快速查找功能，查找操作需要遍历整个堆，时间复杂度为O(n)。

三.堆的代码实现

1.堆的定义

创建一个结构体，其中成员如下：

• array：一个指向整型数组的指针，用于存储堆中的元素。
• capacity：一个整数，表示堆的容量，即 array 数组的最大长度。
• size：一个整数，表示当前堆中的元素个数，即 array 数组中实际存储的元素数量。

typedef struct {int* array;     // 存储堆元素的数组int capacity;   // 堆的容量int size;       // 堆中当前元素的个数
} Heap;

2.创建堆

创建堆。该函数接受一个整数参数 capacity，表示堆的容量。它会分配堆所需的内存，并返回指向堆结构的指针。

// 创建堆
Heap* createHeap(int capacity) {Heap* heap = (Heap*)malloc(sizeof(Heap));heap->array = (int*)malloc(sizeof(int) * capacity);heap->capacity = capacity;heap->size = 0;return heap;
}

3.交换两个数值

交换两个元素的值。该函数接受两个整型指针作为参数，通过引用交换指针所指向的两个整数的值。

// 交换两个元素
void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}

4.入堆

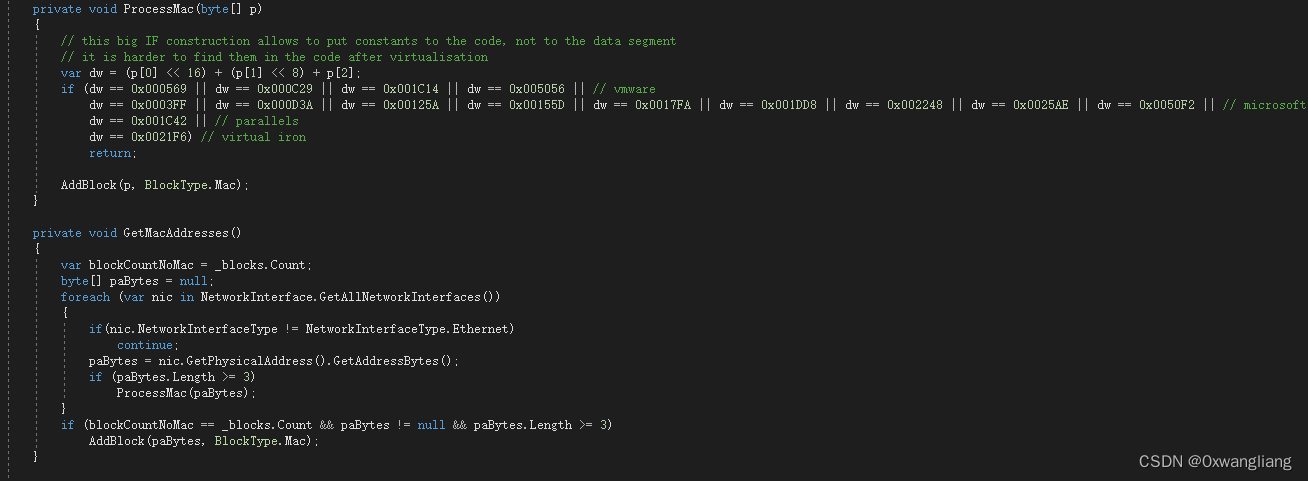
向堆中插入元素。该函数接受一个指向堆结构的指针 heap 和要插入的整数值 value。它将元素插入到堆的最后位置，并通过自上而下的调整操作，保持堆的性质。

// 向堆中插入元素
void insert(Heap* heap, int value) {if (heap->size == heap->capacity) {printf("堆已满，无法插入新元素。\n");return;}// 将新元素插入到堆的最后位置heap->array[heap->size] = value;int currentIndex = heap->size;int parentIndex = (currentIndex - 1) / 2;// 自下而上调整堆结构while (currentIndex > 0 && heap->array[currentIndex] > heap->array[parentIndex]) {swap(&heap->array[currentIndex], &heap->array[parentIndex]);currentIndex = parentIndex;parentIndex = (currentIndex - 1) / 2;}heap->size++;
}

5.出堆

从堆中删除并返回最大元素。该函数接受一个指向堆结构的指针 heap。它将堆顶元素（最大元素）删除，并将最后一个元素移到堆顶，然后通过自上而下的调整操作，保持堆的性质。

// 从堆中删除并返回最大元素
int deleteMax(Heap* heap) {if (heap->size == 0) {printf("堆为空，无法删除元素。\n");return -1;}int maxValue = heap->array[0];// 将最后一个元素移到堆顶heap->array[0] = heap->array[heap->size - 1];heap->size--;int currentIndex = 0;int leftChildIndex = 2 * currentIndex + 1;int rightChildIndex = 2 * currentIndex + 2;// 自上而下调整堆结构while (1) {int maxIndex = currentIndex;// 与左子节点比较if (leftChildIndex < heap->size && heap->array[leftChildIndex] > heap->array[maxIndex]) {maxIndex = leftChildIndex;}// 与右子节点比较if (rightChildIndex < heap->size && heap->array[rightChildIndex] > heap->array[maxIndex]) {maxIndex = rightChildIndex;}// 如果当前节点已经是最大值，则堆已调整完毕if (maxIndex == currentIndex) {break;}// 否则，交换当前节点与最大子节点的位置swap(&heap->array[currentIndex], &heap->array[maxIndex]);currentIndex = maxIndex;leftChildIndex = 2 * currentIndex + 1;rightChildIndex = 2 * currentIndex + 2;}return maxValue;
}

6.打印堆

打印堆元素。该函数接受一个指向堆结构的指针 heap。它会遍历堆中的元素，并将它们打印出来。

// 打印堆元素
void printHeap(Heap* heap) {printf("堆元素：");for (int i = 0; i < heap->size; i++) {printf("%d ", heap->array[i]);}printf("\n");
}

7.销毁堆

释放堆内存。该函数接受一个指向堆结构的指针 heap。它会释放堆所占用的内存，防止内存泄漏。

// 释放堆内存
void destroyHeap(Heap* heap) {free(heap->array);free(heap);
}

四.堆的源码呈现

#include <stdio.h>
#include <stdlib.h>// 定义堆结构
typedef struct {int* array;     // 存储堆元素的数组int capacity;   // 堆的容量int size;       // 堆中当前元素的个数
} Heap;// 创建堆
Heap* createHeap(int capacity) {Heap* heap = (Heap*)malloc(sizeof(Heap));heap->array = (int*)malloc(sizeof(int) * capacity);heap->capacity = capacity;heap->size = 0;return heap;
}// 交换两个元素
void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}// 向堆中插入元素
void insert(Heap* heap, int value) {if (heap->size == heap->capacity) {printf("堆已满，无法插入新元素。\n");return;}// 将新元素插入到堆的最后位置heap->array[heap->size] = value;int currentIndex = heap->size;int parentIndex = (currentIndex - 1) / 2;// 自下而上调整堆结构while (currentIndex > 0 && heap->array[currentIndex] > heap->array[parentIndex]) {swap(&heap->array[currentIndex], &heap->array[parentIndex]);currentIndex = parentIndex;parentIndex = (currentIndex - 1) / 2;}heap->size++;
}// 从堆中删除并返回最大元素
int deleteMax(Heap* heap) {if (heap->size == 0) {printf("堆为空，无法删除元素。\n");return -1;}int maxValue = heap->array[0];// 将最后一个元素移到堆顶heap->array[0] = heap->array[heap->size - 1];heap->size--;int currentIndex = 0;int leftChildIndex = 2 * currentIndex + 1;int rightChildIndex = 2 * currentIndex + 2;// 自上而下调整堆结构while (1) {int maxIndex = currentIndex;// 与左子节点比较if (leftChildIndex < heap->size && heap->array[leftChildIndex] > heap->array[maxIndex]) {maxIndex = leftChildIndex;}// 与右子节点比较if (rightChildIndex < heap->size && heap->array[rightChildIndex] > heap->array[maxIndex]) {maxIndex = rightChildIndex;}// 如果当前节点已经是最大值，则堆已调整完毕if (maxIndex == currentIndex) {break;}// 否则，交换当前节点与最大子节点的位置swap(&heap->array[currentIndex], &heap->array[maxIndex]);currentIndex = maxIndex;leftChildIndex = 2 * currentIndex + 1;rightChildIndex = 2 * currentIndex + 2;}return maxValue;
}// 打印堆元素
void printHeap(Heap* heap) {printf("堆元素：");for (int i = 0; i < heap->size; i++) {printf("%d ", heap->array[i]);}printf("\n");
}// 释放堆内存
void destroyHeap(Heap* heap) {free(heap->array);free(heap);
}int main() {Heap* heap = createHeap(10);insert(heap, 5);insert(heap, 8);insert(heap, 2);insert(heap, 10);insert(heap, 3);printHeap(heap);int max = deleteMax(heap);printf("删除的最大元素：%d\n", max);printHeap(heap);destroyHeap(heap);return 0;
}